The document covers key concepts in network security, focusing on asymmetric key cryptography including RSA and OAEP, along with factors involved in public key cryptography. It discusses the vulnerabilities of textbook RSA, implementation attacks, and the significance of using secure key lengths and preprocessing functions to enhance security. Key methodologies such as prime factorization, secure message authentication, and the Diffie-Hellman key exchange are also outlined.

1. Network Security
CS-7 (CH13-14)
By: Prof. Ganesh Ingle

2. Session 2 objective
CS-6 Revision Previous Session revision
CS -7 Model of Asymmetric Key Cryptography
CS – 7 Factorization and other methods for Public Key
Cryptography
CS -7 RSA and OAEP
CS-7 Diffe-Hellman Key Exchange and its Security Aspects
SUMMARY

3. CS -7 Message authentication & types
Model of Asymmetric Key Cryptography

4. CS -7 Message authentication & types
Model of Asymmetric Key Cryptography

5. Factors
 Factors are the numbers you multiply together to get a
product.
 For example, the product 24 has several factors.
 24 = 1 x 24
 24 = 2 x 12
 24 = 3 x 8
 24 = 4 x 6
 SO, the factors are 1, 2, 3, 4, 6, 8, 12, 24
CS -7 Factorization & other methods for PK Cryptography

6. Finding Factors
 Start with 1 times the number.
 Try 2, 3, 4, etc.
 When you repeat your factors, cross out the repeat -
you’re done at this point.
 If you get doubles (such as 4 x 4), then you’re done.
Repeats or doubles let you know you’re done.
CS -7 Factorization & other methods for PK Cryptography

7. What are the factors of 16?
1 x 16
2 x 8
3 x ?? 3 is not a factor, so cross it out
4 x 4 doubles = done
The factors of 16 are
1,2,4,8,16
CS -7 Factorization & other methods for PK Cryptography

8. Prime and Composite Numbers
Prime numbers are
numbers that only have
two factors: one, and the
number itself.
EXAMPLES:
3, 5, 7, 11, 31
Composite numbers
have more than two
factors.
EXAMPLES:
6, 15, 18, 30, 100
CS -7 Factorization & other methods for PK Cryptography

9. Example: Prime Factorization of 100.
100
2 X 50
100 ÷ 2 = 50. Two is
the first prime number
that goes into 100.
2 is a prime
number, so we are
done with it.
Now we deal with the
50. Divide it by 2 to get
the next factors.
2 X 25
25 is not divisible by
the first prime, 2. The
next prime, 3, does not
work either. We must
divide by 5 to get a
factor.
5 x 5
Both numbers are prime,
leaving us with all primes.
CS -7 Factorization & other methods for PK Cryptography

10. CS -7 RSA and OAEP

11. CS-7 Diffe-Hellman Key Exchange and its Security Aspects

12. The RSA cryptosystem
 First published:
 Scientific American, Aug. 1977.
(after some censorship entanglements)
 Currently the “work horse” of Internet security:
 Most Public Key Infrastructure (PKI) products.
 SSL/TLS: Certificates and key-exchange.
 Secure e-mail: PGP, Outlook, …
Page
12
CS -7 RSA and OAEP

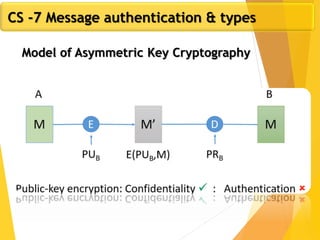
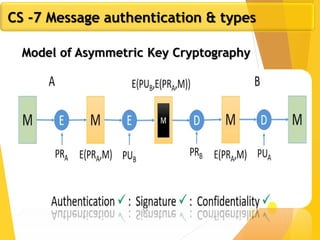
13. The RSA trapdoor 1-to-1 function
 Parameters: N=pq. N 1024 bits. p,q 512 bits.
e – encryption exponent. gcd(e, (N) ) = 1 .
 1-to-1 function: RSA(M) = Me
(mod N) where MZN
*
Page
13
 Trapdoor: d – decryption exponent.
Where ed = 1 (mod (N) )
 Inversion: RSA(M)d
= Med
= Mk(N)+1
= M (mod N)
 (n,e,t,)-RSA Assumption: For any t-time alg. A:
Pr[ A(N,e,x) = x
1/e
(N) : ]< 
p,q  n-bit primes,
Npq, xZN
*
R
R
CS -7 RSA and OAEP

14. Textbook RSA is insecure
 Textbook RSA encryption:
 public key: (N,e) Encrypt: C = M
e
(mod N)
 private key: d Decrypt: Cd
= M (mod N)
(M  ZN
* )
 Completely insecure cryptosystem:
 Does not satisfy basic definitions of security.
 Many attacks exist.
 The RSA trapdoor permutation is not a cryptosystem !
Page
14
CS -7 RSA and OAEP

15. A simple attack on textbook RSA
 Session-key K is 64 bits. View K  {0,…,264} Eavesdropper sees:
C = Ke
(mod N) .
 Suppose K = K1K2 where K1, K2 < 234 . (prob. 20%) Then: C/K1
e
=
K2
e
(mod N)
 Build table: C/1e, C/2e, C/3e, …, C/234e . time: 234
For K2 = 0,…, 234 test if K2
e
is in table. time: 23434
 Attack time: 240 << 264
Page
15
Web
Browser
Web
Server
CLIENT HELLO
SERVER HELLO (e,N) d
C=RSA(K)
Rando
m
session-
key K
CS -7 RSA and OAEP

16. Common RSA encryption
 Never use textbook RSA.
 RSA in practice:
 Main question:
 How should the preprocessing be done?
 Can we argue about security of resulting system?
Page
16
msg
Preprocessing
ciphertext
RSA
CS -7 RSA and OAEP

17. PKCS1 V1.5
 PKCS1 mode 2: (encryption)
 Resulting value is RSA encrypted.
 Widely deployed in web servers and browsers.
 No security analysis !!
Page
17
02 random pad FF msg
1024 bits
16 bits
CS -7 RSA and OAEP

18. Attack on PKCS1
 Bleichenbacher 98. Chosen-ciphertext attack.
 PKCS1 used in SSL:
 attacker can test if 16 MSBs of plaintext = ’02’.
 Attack: to decrypt a given ciphertext C do:
 Pick r  ZN. Compute C’ = reC = (r  PKCS1(M))
e
.
 Send C’ to web server and use response.
AttackerWeb
Server
dIs this
PKCS1?
ciphertextC=
C
Yes: continue
No: error02
CS -7 RSA and OAEP

19. Chosen ciphertext security (CCS)
 No efficient attacker can win the following game:
 (with non-negligible advantage)
Page
19
AttackerChallenger
M0, M1
b’{0,1}
Attacker wins if b=b’
C=E(Mb) bR{0,1}
Challenge
Decryptio
n oracle
C
CS -7 RSA and OAEP

20. PKCS1 V2.0 - OAEP
 New preprocessing function: OAEP (BR94).
 Thm: RSA is trap-door permutation  OAEP is CCS
when H,G are “random oracles”.
 In practice: use SHA-1 or MD5 for H and G.
Page
20
H+
G +
Plaintext to encrypt with RSA
rand.M 01 00..0
Check pad
on decryption.
Reject CT if invalid.
{0,1}n-1
CS -7 RSA and OAEP

21. OAEP Improvements
 OAEP+: (Shoup’01)
 trap-door permutation F
F-OAEP+ is CCS when
H,G,W are “random oracles”.
 SAEP+: (B’01)
RSA trap-door perm 
RSA-SAEP+ is CCS when
H,W are “random oracle”.
Page
21
R
H+
G +
M W(M,R)
R
H+
M W(M,R)
CS -7 RSA and OAEP

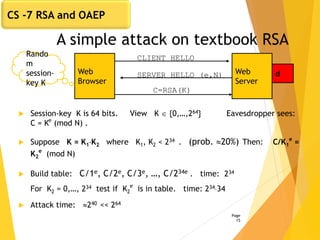
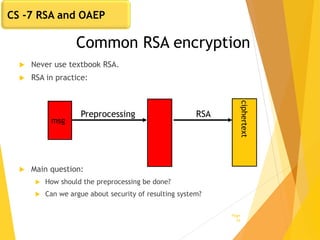
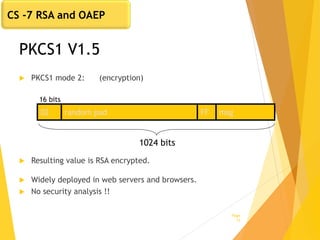
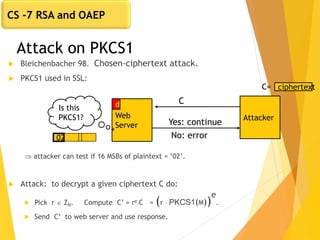
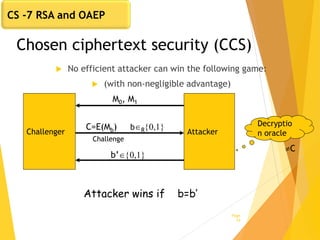
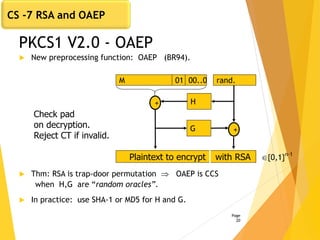
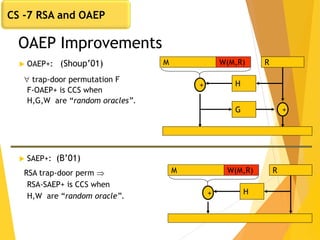
22. Subtleties in implementing OAEP [M ’00]
OAEP-decrypt(C) {
error = 0;
if ( RSA-1
(C) > 2n-1
)
{ error =1; goto exit; }
if ( pad(OAEP-1
(RSA-1
(C))) != “01000” )
{ error = 1; goto exit; }
Page
22
}
 Problem: timing information leaks type of error.
 Attacker can decrypt any ciphertext C.
 Lesson: Don’t implement RSA-OAEP yourself …
CS -7 RSA and OAEP

23. Is RSA a one-way permutation?
 To invert the RSA one-way function (without d) attacker must compute:
M from C = Me
(mod N).
 How hard is computing e’th roots modulo N ??
 Best known algorithm:
 Step 1: factor N. (hard)
 Step 2: Find e’th roots modulo p and q. (easy)
Page
23
CS -7 RSA and OAEP

24. Shortcuts?
 Must one factor N in order to compute e’th roots?
Exists shortcut for breaking RSA without factoring?
 To prove no shortcut exists show a reduction:
 Efficient algorithm for e’th roots mod N
 efficient algorithm for factoring N.
 Oldest problem in public key cryptography.
 Evidence no reduction exists: (BV’98)
 “Algebraic” reduction  factoring is easy.
 Unlike Diffie-Hellman (Maurer’94).
Page
24
CS -7 RSA and OAEP

25. Improving RSA’s performance
 To speed up RSA decryption use
small private key d. C
d
= M (mod N)
 Wiener87: if d < N0.25 then RSA is insecure.
 BD’98: if d < N0.292 then RSA is insecure
(open: d < N0.5
)
 Insecure: priv. key d can be found from (N,e).
 Small d should never be used.
Page
25
CS -7 RSA and OAEP

26. Wiener’s attack
 Recall: ed = 1 (mod (N) )
  kZ : ed = k(N) + 1

(N) = N-p-q+1  |N- (N)|  p+q  3N
d  N0.25/3 
Continued fraction expansion of e/N gives k/d.
ed = 1 (mod k)  gcd(d,k)=1
Page
26
e
(N)
k
d
- 
1
d(N)
e
N
k
d
- 
1
2d2
CS -7 RSA and OAEP

27. RSA With Low public exponent
 To speed up RSA encryption (and sig. verify)
use a small e. C = Me (mod N)
 Minimal value: e=3 ( gcd(e, (N) ) = 1)
 Recommended value: e=65537=216+1
Encryption: 17 mod. multiplies.
 Several weak attacks. Non known on RSA-OAEP.
 Asymmetry of RSA: fast enc. / slow dec.
 ElGamal: approx. same time for both.
Page
27
CS -7 RSA and OAEP

28. Implementation attacks
 Attack the implementation of RSA.
 Timing attack: (Kocher 97)
The time it takes to compute C
d
(mod N)
can expose d.
 Power attack: (Kocher 99)
The power consumption of a smartcard while
it is computing C
d
(mod N) can expose d.
 Faults attack: (BDL 97)
A computer error during Cd
(mod N)
can expose d.
Page
28OpenSSL defense: check output. 5% slowdown.
CS -7 RSA and OAEP

29. Key lengths
 Security of public key system should be comparable to security of
block cipher.
NIST:
Cipher key-size Modulus size
 64 bits 512 bits.
80 bits 1024 bits
128 bits 3072 bits.
256 bits (AES) 15360 bits
 High security  very large moduli.
Not necessary with Elliptic Curve Cryptography.
Page
29
CS -7 RSA and OAEP

30. Thank you
Image Source
searchenterpriseai.techtarget.com
wikipedia