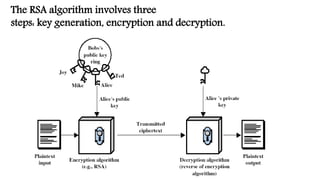
RSA is an asymmetric cryptographic algorithm used for encrypting and decrypting messages. It uses a public key for encryption and a private key for decryption such that a message encrypted with the public key can only be decrypted with the corresponding private key. The RSA algorithm involves three steps: key generation, encryption, and decryption. It addresses issues of key distribution and digital signatures.

1. Mr . Sathish Kumar . M
Department of Electronics and Communication
Engineering
I’ve learned that people will forget what you said, people will forget
what you did, but people will never forget how you made them feel.
–Maya Angelou

2. RivestShamir& Adleman
MIT in 1977

3. What is RSA…?
• RSA is an algorithm used by modern computers
to encrypt and decrypt messages.
• It is an asymmetric cryptographic algorithm.
• It is included as part of the Web browsers from
Microsoft and Netscape.
• It's also part of Lotus Notes, Intuit's Quicken, and many
other products.

4. RSA
PUBLIC KEY PRIVATE KEY
Public-key
cryptography, also
known as asymmetric
cryptography, is a
class
of cryptographic
algorithms
Messages encrypted
using the public key
can only be
decrypted with the
private key.

6. OPERATION:
• RSA involves a public key and private key.
• The public key can be known to everyone, it is used to encrypt
messages.
• Messages encrypted using the public key can only be decrypted
with the private key.
The public key is used for encryption.
• The key is known to the public .
• The private key is used for decryption.
• The key is only known to the
owner .

7. The RSA algorithm involves three
steps: key generation, encryption and decryption.

8. Why RSA…?
• It developed to address two key issues:
• Key distribution – how to have secure
communications in general without having to
trust a KDC with your key
• Digital signatures – how to verify a message
comes intact from the claimed sender

10. RSA CHARACTERISTICS:
 Public-Key algorithms rely on two keys with the characteristics
that it is:
 computationally infeasible to find decryption key knowing
only algorithm & encryption key
 computationally easy to en/decrypt messages when the
relevant (en/decrypt) key is known
 either of the two related keys can be used for encryption,
with the other used for decryption (in some schemes)

12. One-way function with trapdoor
f
x y
x y
x y

f

1

f

1

trapdoor
Easy:
Hard:
Easy:
Use trapdoor
as the private key.
Many public-key cryptosystems are
based on trapdoor one-way fu

nctions.

13. RSA

1
RSA

Idea behind RSA
*
It works in group
Z
Encryption (easy):
Decryption (hard):
Looking for a trapdoor: ( ) .
If is a number such that 1mod ( ), then
( )
1
.
e
e
e d
n
x x
x x
x x
d ed n
e d k
n





 
k
for some , and
  ( ) 1 ( )
k
e d ed n k n
x x x x x x x          
( ) 1 .

14. Integers
a b a b a b

| : divides , is a divisor of .

gcd( a , b ): greatest common divisor of a and b
.
 Coprime or relatively prime: gcd( a , b
) 
1.

Euclid's algorithm: computes gcd( a , b
).
 Extented Eucl
id's algorithm: computes integers
x and y such that ax  by  gcd(a,b).

15. Euler Totient Function ø(n)
• when doing arithmetic modulo n
• complete set of residues is: 0..n-1
• reduced set of residues is those numbers (residues) which are
relatively prime to n
eg for n=10,
• complete set of residues is {0,1,2,3,4,5,6,7,8,9}
• reduced set of residues is {1,3,7,9}
• number of elements in reduced set of residues is called the Euler
Totient Function ø(n)

16. Euler Totient Function ø(n)
• when doing arithmetic modulo n
• complete set of residues is: 0..n-1
• reduced set of residues is those numbers (residues) which are
relatively prime to n
• eg for n=10,
• complete set of residues is {0,1,2,3,4,5,6,7,8,9}
• reduced set of residues is {1,3,7,9}
• number of elements in reduced set of residues is called the
Euler Totient Function ø(n)

17. Euler Totient Function ø(n)
• when doing arithmetic modulo n
• complete set of residues is: 0..n-1
• reduced set of residues is those numbers (residues) which
are relatively prime to n
eg for n=10,
• complete set of residues is {0,1,2,3,4,5,6,7,8,9}
• reduced set of residues is {1,3,7,9}
• number of elements in reduced set of residues is called the
Euler Totient Function ø(n)

18. RSA ALGORITH EXAMPLE
Choose p = 3 and q = 11
Compute n = p * q = 3 * 11 = 33
Compute φ(n) = (p - 1) * (q - 1) = 2 * 10 = 20
Choose e such that 1 < e < φ(n) and e and n are coprime. Let e = 7
Compute a value for d such that (d * e) % φ(n) = 1. One solution is d = 3 [(3 *
7) % 20 = 1]
Public key is (e, n) => (7, 33)
Private key is (d, n) => (3, 33)
The encryption ofm = 2 isc = 27 % 33 = 29
The decryption ofc = 29 ism = 293 % 33 = 2