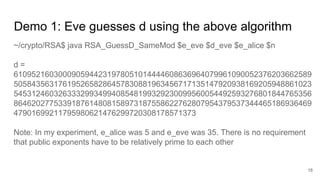
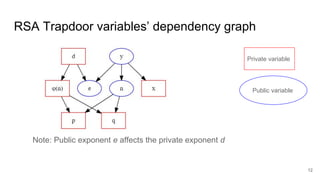
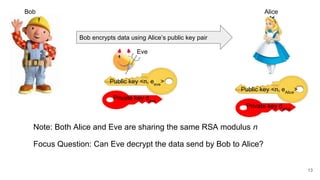
This document analyzes the security implications of sharing the same RSA modulus n between two users. It presents three algorithms that an attacker could use to break RSA encryption if the public keys for two users share the same n value. Algorithm 1 works if the public exponents are relatively prime. Algorithm 2 works for small public exponents by factoring n. Algorithm 3 directly factors n from the private exponent. The conclusion is that RSA is breakable if n is not unique per user.

1. Analysis of shared RSA Modulus n
Dr. Dharma Ganesan, Ph.D.,

2. Disclaimer
● The opinions expressed here are my own
○ But not the views of my employer
● The source code fragments and exploits shown here can be reused
○ But without any warranty nor accept any responsibility for failures
● Do not apply the exploit discussed here on other systems
○ Without obtaining authorization from owners
2

3. Question (notations are defined later)
● An RSA public key is made of two public variables <n, e>
● If n is shared between two users, can we break RSA?
● If <n, e1
> and <n, e2
> are public keys, we break RSA
● We make no assumption about e1
and e2
3

4. Agenda
● Brief overview of RSA algorithm
● Formal definition of RSA Trapdoor function
● Algorithms and Demos
● Conclusion
4

5. Prerequisite
Some familiarity with the following topics will help to follow the rest of the slides
● Group Theory
● Number Theory
● Algorithms and Complexity Theory
● If not, it should still be possible to obtain a high-level overview
5

6. How can Bob send a message to Alice securely?
6
Public Key PuA
● Alice and Bob never met each other
● Bob will encrypt using Alice’s public key
○ Assume that public keys are known to the world
● Alice will decrypt using her private key
○ Private keys are secrets (never sent out)
● Bob can sign messages using his private key
○ Alice verifies message integrity using Bob’s public key
○ Not important for this presentation/attack
● Note: Alice and Bob need other evidence (e.g., passwords,
certificates) to prove their identity to each other
● Who are Alice, Bob, and Eve?
Private Key PrA
Public Key PuB
Private Key PrB

7. RSA Public Key Cryptography System
● Published in 1977 by Ron Rivest, Adi Shamir and Leonard Adleman
● Rooted in elegant mathematics - Group Theory and Number Theory
● Core idea: Anyone can encrypt a message using recipient's public key but
○ (as far as we know) no one can efficiently decrypt unless they got the matching private key
● Encryption and Decryption are inverse operations (math details later)
○ Work of Euclid, Euler, and Fermat provide the mathematical foundation of RSA
● Eavesdropper Eve cannot easily derive the secret (math details later)
○ Unless she solves “hard” number theory problems that are computationally intractable
7

8. 8
Notations and Facts
GCD(x, y): The greatest common divisor that divides integers x and y
Co-prime: If gcd(x, y) = 1, then x and y are co-primes
Zn
= { 0, 1, 2, …, n-1 }, n > 0; we may imagine Zn
as a circular wall clock
Z*
n
= { x ∈ Zn
| gcd(x, n) = 1 }; (additional info: Z*
n
is a multiplicative group)
φ(n): Euler’s Totient function denotes the number of elements in Z*
n
φ(nm) = φ(n).φ(m) (This property is called multiplicative)
φ(p) = p-1, if p is a prime number

9. Notations and Facts ...
● x ≡ y (mod n) denotes that n divides x-y; x is congruent to y mod n
● Euler’s Theorem: aφ(n)
≡ 1 (mod n), if gcd(a, n) = 1
● Fermat’s Little Theorem: ap
≡ a (mod p)
● Gauss’s Fundamental Theorem of Arithmetic: Any integer greater than 1 is
either a prime or can be written as a unique product of primes
○ Euclid’s work is the foundation for this theorem, see The Elements
● Euclid’s Lemma: if a prime p divides the product of two natural numbers a
and b, then p divides a or p divides b
● Euclid’s Infinitude of Primes (c. 300 BC): There are infinitely many primes
9

10. RSA - Key Generation Algo
1. Select an appropriate bitlength of the RSA modulus n (e.g., 2048 bits)
○ Value of the parameter n is not chosen until step 3; small n is dangerous (details later)
2. Pick two independent, large random primes, p and q, of half of n’s bitlength
○ In practice, p and q satisfy q < p < 2q to avoid polynomial time factorization algorithms
3. Compute n = p.q (n is also called the RSA modulus)
4. Compute Euler’s Totient (phi) Function φ(n) = φ(p.q) = φ(p)φ(q) = (p-1)(q-1)
5. Select numbers e and d from Zn
such that e.d ≡ 1(mod φ(n))
○ e must be relatively prime to φ(n) otherwise d cannot exist (i.e., we cannot decrypt)
○ d is the multiplicative inverse of e in Zn
6. Public key is the pair <n, e> and private key is 4-tuple <φ(n), d, p, q>
10

11. RSA Trapdoor
● RSA: Zn
→ Zn
● Let x and y ∈ Zn
● y = RSA(x) = xe
mod n
○ We may view x as a plaintext, and y as the corresponding ciphertext
● x = RSA-1
(y) = yd
mod n
● e and d are also called encryption and decryption exponents, respectively
11

12. RSA Trapdoor variables’ dependency graph
12
Private variable
Public variable
Note: Public exponent e affects the private exponent d

13. 13
Public key <n, eAlice
>
Public key <n, eeve
>
AliceBob
Eve
Bob encrypts data using Alice’s public key pair
Note: Both Alice and Eve are sharing the same RSA modulus n
Focus Question: Can Eve decrypt the data send by Bob to Alice?
Private key dalice
Private key deve

14. 14
Formal Problem Statement
Bob encrypts secret 𝓍 using Alice’s public key <n, ealice
>, which she can decrypt
using dalice
Bob computes y = RSA( 𝓍) and send to Alice using her public exponent ealice
Can Eve reconstruct 𝓍 using her private exponent deve
and public exponent ealice
?
Note that both Eve and Alice share the same RSA public modulus n but they have
different public exponents eeve
and ealice
, respectively
Further, assume that Eve does not know φ(n); otherwise, it is a piece of cake (?)

15. Solutions - Three different cryptanalysis algorithms
Eve has at least three different ways to break RSA when n is shared
Let V = eeve
deve
- 1
Algorithm 1: Lucky case: ealice
is relatively prime to V
Algorithm 2: If ealice
is not relatively prime to V, Eve can try a variant of solution 1
Algorithm 3: Derive prime factors p and q from deve
15

16. Algorithm 1: In case ealice
is relatively prime to V
We known eeve
.deve
≡ 1(mod φ(n)); Thus, V = eeve
.deve
- 1 is a multiple of φ(n)
Since ealice
is relatively prime to V, Eve can find d from the following:
ealice
.d ≡ 1(mod V) ⇒ ealice
.d = 1 + kV for some integer k.
Eve will use this d to decrypt the ciphertext y send from Bob to Alice as follows:
yd
mod n = ( 𝓍 ) mod n = 𝓍1+kV
mod n = 𝓍 𝓍kV
mod n = 𝓍 mod n; [Note 𝓍kV
mod n
= 1;Euler’s theorem]
Thus, Eve got the secret message 𝓍 by simply performing yd
mod n
16
ealice
d

17. Demo 1
17
Bob sends to alice “How are you?” encrypted using her public key ealice
= 5
(as an example)
~/crypto/RSA$ java RSA_Encrypt $n $e_alice "How are you?"
Output ciphertext y=
76dc17aa07343da5366c5ae5f2ea14f42e3016ad8e9f05e7ac70b3bb38ce8ea
962543d2941ff53f0957a5bb6bdae0d6a08eaa8f89154cc5331aa3f

18. Demo 1: Eve guesses d using the above algorithm
18
~/crypto/RSA$ java RSA_GuessD_SameMod $e_eve $d_eve $e_alice $n
d =
6109521603000905944231978051014444608636964079961090052376203662589
5058435631761952658286457830881963456717135147920938169205948861023
5453124603263332993499408548199329230099560054492593276801844765356
8646202775339187614808158973187558622762807954379537344465186936469
47901699211795980621476299720308178571373
Note: In my experiment, e_alice was 5 and e_eve was 35. There is no requirement
that public exponents have to be relatively prime to each other

19. 19
public static BigInteger guessD(BigInteger e_eve, BigInteger d_eve, BigInteger e_alice,
BigInteger n) {
BigInteger one = BigInteger.ONE;
BigInteger v = e_eve.multiply(d_eve).subtract(one);
assert e_alice.gcd(v).equals(one);
BigInteger d = e_alice.modInverse(v);
return d;
}

20. Demo 1: Eve successfully decrypts
20
~/crypto/RSA$ java RSA_Decrypt $n $d $y
Output:
Plaintext: How are you?

21. Algorithm 2: In case ealice
is not relatively prime to V
21
eeve
.deve
≡ 1(mod φ(n)) ⇒ eeve
.deve
-1 = k φ(n) for some unknown integer k
Let V = eeve
.deve
-1 ⇒ V = k φ(n)
φ(n) = (p-1)(q-1)
kφ(n) = k(pq - p - q + 1)
kp2
- (kn+ k - kφ(n))p + kn = 0 (since n = pq and V = k φ(n))
kp2
- (kn+ k - V)p + kn = 0
This is a quadratic equation in p. We know how to solve ax2
+bx+c = 0.
Note also that the product of the two roots = c/a = kn/k = n. Thus the products
of the roots are the prime factors of n

22. Algorithm 2: In case ealice
is not relatively prime to V
22
There is one challenge in Algorithm 2: We do not know the value of K
However, we can prove that k < eeve
(general proof on the next slide)
This means that if eeve
is not a very large number, we can try different values of k
For example, in my experiments eeve
is bounded by 65537, which is a
recommended value of e

23. 23
Fact: If ed - 1 = k φ(n), then k < e
Proof (by contradiction):
Suppose k > e then ed - 1 > e φ(n)
Since ed > ed - 1 > eφ(n) ⇒ ed > e φ(n)
Since e > 0, divide by e to obtain d > φ(n);
This is a contradiction because RSA private exponent d is smaller than φ
(n). Note: One can similarly prove that k < d, too.

24. 24

25. 25
~/crypto/RSA$ java PrimeFactorsSameMod $e_eve $d_eve $n
p =
13276679695761958519526349357562244988244279824926936082195687
40853247578889768050764104271700195002296832080914965123511352
0731128590296162806037862841243
q =
95868623013590057413914082440137643220393917593508351868252918
43518030624838461380195946775818574653366607424324589728945776
902488108182844666775027068559
Demo 2: Eve derives factors p and q from her deve

26. Algorithm 3: Factorize n from deve
26
We know that eeve
.deve
≡ 1(mod φ(n))
eeve
.deve
- 1 ≡ 0 ( mod φ(n)) ⇒ eeve
.deve
- 1 = r φ(n) for some integer r.
Let k = eeve
.deve
- 1. This means that k is a multiple of φ(n). K is even because φ(n) is
even
Let g be a random element of Z*
n
. That is, g is relatively prime to n.
Euler’s theorem says gk
≡ 1 (mod n) since gcd (g, n) =1 .
This implies gk/2
is a square of one mod n because gk/2
. gk/2
= gk
≡ 1 (mod n)

27. Algorithm 3: Factorize n from deve
27
Step 1: Pick a random g from the multiplicative group Zn
*
Step 2: Construct a sequence: gk/2
, gk/4
, gk/8
, … until not equal to 1 mod n
Note: If k/2i
is not an even number, go back to step 1 and pick a new g
Step 3: Now we have calculated square root of one in mod n.
That is, z2
≡ 1 (mod n) and z ≠ ∓ 1 (mod n)
(z+1)(z-1) ≡ 0 (mod n)
This implies n divides (z+1) and (z-1).
Equivalently, n must share factors with (z+1) and (z-1).
Step 4: Compute gcd(n, z-1) to extract one of the prime factors (say p) of n
Step 5: Derive another prime factor q = n/p

28. 28
My implementation of the
algorithm to find the prime
factors p and q from d

29. 29
~/crypto/RSA$ java PrimeFactorsFromD $e_eve $d_eve $n
p =
95868623013590057413914082440137643220393917593508351868252918435180
30624838461380195946775818574653366607424324589728945776902488108182
844666775027068559
q =
13276679695761958519526349357562244988244279824926936082195687408532
47578889768050764104271700195002296832080914965123511352073112859029
6162806037862841243
Example: Derive the prime factors p and q from deve

30. Conclusion
30
● If RSA public modulus n is not unique per user, then RSA is breakable
● We investigated three different cryptanalysis algorithms to break
○ Algorithm 1 is efficient if public exponents have certain math properties
○ Algorithm 2 relaxes the properties but works only for “small” public exponents
○ Algorithm 3 works well even for very large public exponents, too
● Algorithm 2 is the slowest of all because it enumerates an unknown variable
● Algorithm 3 is efficient in general - no restriction on the public exponent values
● Takeaway is that <n, e1
>, <n, e2
> should not be part of the system
○ The public exponent e can be shared among the participants though.

31. References
● W. Diffie and M. E. Hellman, “New Directions in Cryptography,” IEEE
Transactions on Information Theory, vol. IT-22, no. 6, November, 1976.
● R. L. Rivest, A. Shamir, and L. Adleman, “A method for obtaining digital
signatures and public-key cryptosystems,” CACM 21, 2, February, 1978.
● A. Menezes, P. van Oorschot, and S. Vanstone, “Handbook of Applied
Cryptography,” CRC Press, 1996.
● C. Paar and J. Pelzl. “Understanding Cryptography: A Textbook for Students
and Practitioners,” Springer, 2011.
31