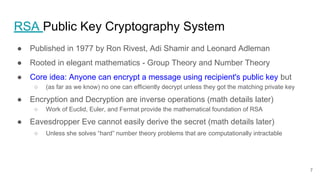
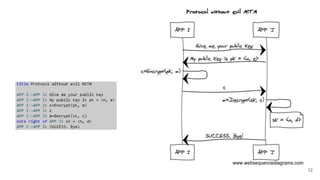
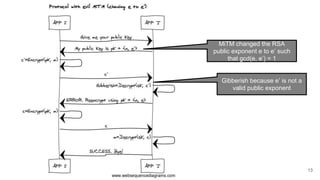
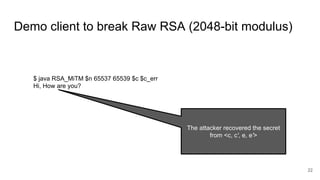
The presentation explains how to break unauthenticated RSA encryption by employing man-in-the-middle attacks to modify public exponents, allowing attackers to recover plaintext from ciphertext. It details the use of the extended Euclidean algorithm in the attack method, emphasizing the risks of using RSA without integrity checks or digital signatures. The findings highlight that such vulnerabilities can persist in systems employing public-key cryptography if proper safeguards are not implemented.

1. Experiments on RSA
without integrity checks
Demo of Reversing the Plaintexts from the Ciphertexts
Dr. Dharma Ganesan, Ph.D.,

2. Disclaimer
● The opinions expressed here are my own
○ But not the views of my employer
● The source code fragments and exploits shown here can be reused
○ But without any warranty nor accept any responsibility for failures
● Do not apply the exploit discussed here on other systems
○ Without obtaining authorization from owners
2

3. Goal of this presentation (details later)
● Explain how to break unauthenticated RSA
○ That is, RSA without digital signature/integrity checks
● Present exploit: Man-in-the-middle edit public exponents
○ Uses Bézout’s theorem to recover the plaintexts from ciphertexts
○ Extended Euclidean Algorithm is the core
● This challenge was given to me by a friend who works for
a social media giant
3

4. Informal system design and constraints for attackers
● A set of apps send data to each other using public-key cryptography (RSA)
○ App i uses the public key of app j to send encrypted data to app j
○ Apps send public keys over public channels, without digital signature/certificate
● The attackers are allowed to edit only the RSA public exponent e
● The attackers cannot impersonate any app nor inject their own apps
● Goal: Reverse the plaintext from the ciphertext, satisfying the constraints
4

5. Prerequisite (to follow the remaining slides)
Some familiarity with the following topics will help to follow the rest of the slides
● Group Theory (Abstract Algebra/Discrete Math)
● Modular Arithmetic (Number Theory)
● Algorithms and Complexity Theory
● If not, it should still be possible to obtain a high-level overview
5

6. How can Bob send a message to Alice securely?
6
Public Key PuA
● Alice and Bob never met each other
● Bob will encrypt using Alice’s public key
○ Assume that public keys are known to the world
● Alice will decrypt using her private key
○ Private keys are secrets (never sent out)
● Bob can sign messages using his private key
○ Alice verifies message integrity using Bob’s public key
○ Not important for this presentation/attack
● Note: Alice and Bob need other evidence (e.g., passwords,
certificates) to prove their identity to each other
Private Key PrA
Public Key PuB
Private Key PrB

7. RSA Public Key Cryptography System
● Published in 1977 by Ron Rivest, Adi Shamir and Leonard Adleman
● Rooted in elegant mathematics - Group Theory and Number Theory
● Core idea: Anyone can encrypt a message using recipient's public key but
○ (as far as we know) no one can efficiently decrypt unless they got the matching private key
● Encryption and Decryption are inverse operations (math details later)
○ Work of Euclid, Euler, and Fermat provide the mathematical foundation of RSA
● Eavesdropper Eve cannot easily derive the secret (math details later)
○ Unless she solves “hard” number theory problems that are computationally intractable
7

8. 8
Notations and Facts
GCD(x, y): The greatest common divisor that divides integers x and y
Co-prime: If gcd(x, y) = 1, then x and y are co-primes
Zn
= { 0, 1, 2, …, n-1 }, n > 0; we may imagine Zn
as a circular wall clock
Z*
n
= { x ∈ Zn
| gcd(x, n) = 1 }; (additional info: Z*
n
is a multiplicative
group)
φ(n): Euler’s Totient function denotes the number of elements in Z*
n
φ(p) = p-1, if p is a prime number
x ≡ y (mod n) denotes that n divides x-y; x is congruent to y mod n

9. Bézout’s identity (needed later for this attack)
● Let a and b are two integers. There exists a pair of integers x and y such that:
○ a.x + b.y = gcd(a, b)
● If a and b are relatively prime to each other, then
○ a.x + b.y = 1
● For a given a and b, we use the Extended Euclidean Algorithm to find x and y
9

10. RSA - Key Generation Algo. (Fits on one page)
1. Select an appropriate bitlength of the RSA modulus n (e.g., 2048 bits)
○ Value of the parameter n is not chosen until step 3; small n is dangerous (details later)
2. Pick two independent, large random primes, p and q, of half of n’s bitlength
○ In practice, p and q are not close to each other to avoid attacks (e.g., Fermat’s factorization)
3. Compute n = p.q (n is also called the RSA modulus)
4. Compute Euler’s Totient (phi) Function φ(n) = φ(p.q) = φ(p)φ(q) = (p-1)(q-1)
5. Select numbers e and d from Zn
such that e.d ≡ 1(mod φ(n))
○ Many implementations set e to be 65537 (Note: gcd(e, φ(n)) = 1)
○ e must be relatively prime to φ(n) otherwise d cannot exist (i.e., we cannot decrypt)
○ d is the multiplicative inverse of e in Zn
6. Public key is the pair <n, e> and private key is 4-tuple <φ(n), d, p, q>
Note: If p, q, d, or φ(n) is leaked, RSA is broken immediately
10

11. Formal definition of the RSA trapdoor function
● RSA: Zn
→ Zn
● Let m and c ∈ Zn
● c = RSA(m) = me
mod n
● m = RSA-1
(c) = cd
mod n
● e and d are also called encryption and decryption
exponents, respectively
● Note: Attackers know c, e, and n but not d
11

12. 12

13. 13
MiTM changed the RSA
public exponent e to e’ such
that gcd(e, e’) = 1
Gibberish because e’ is not a
valid public exponent

14. Core idea of the attack
● The attacker corrupts the public exponent e
● Instead of the standard exponent e = 65537, she modifies to e' = 65539
● Note that gcd(e, e') = 1
● They both are relatively prime to each other
● The receiver will get gibberish during decryption because of the corrupted e
● The receiver will resend the same public key pair <n, e>
● The sender will re-encrypt the same message using the public key pair
● Now the attacker does not modify the public key pair
14

15. Core idea of the attack …
● The attacker has two ciphertext pair:
● c' which is the ciphertext produced by the sender using e'
● c which is the ciphertext produced by the sender using correct e
● Goal of the attacker is to recover the plaintext m from <c, c', e, e'>
15

16. Algorithm: Recover the plaintext m from <c, c', e, e'>
● To recover m, the attacker applies the Extended Euclidean Algorithm:
● Since gcd(e, e' ) = 1, there must exist x and y such that e.x + e'.y = 1
● We can prove that the plaintext m = cx
. (c' )y
mod n
○ cx
= (me
)x
mod n
○ (c')y
= (me'
)y
mod n
○ cx
. (c' )y
= (me
)x
mod n . (me'
)y
mod n
= m(ex + e' y)
mod n = m
● Summary: The attacker recovered m from <c, c', e, e', x, y>
16

17. Implementation of the algorithm
17
public static BigInteger reversePlaintext(BigInteger n, BigInteger e,
BigInteger e_err, BigInteger c, BigInteger c_err) {
BigIntEuclidean bigIntEuclidean = BigIntEuclidean.calculate(e, e_err);
BigInteger x = bigIntEuclidean.x;
BigInteger y = bigIntEuclidean.y;
BigInteger part1 = c.modPow(x, n);
BigInteger part2 = c_err.modPow(y, n);
BigInteger result = part1.multiply(part2).mod(n);
return result;
}
Mapping of variables to the algorithm:
c_err → c‘
e_err → e‘
part1 → cx
part2 → (c')y
BigIntEuclidean class implements
the Extended Euclidean Algorithm

18. Slide demo
18

19. Captured public key <n, e>
19
n =
18004824506648204194492044002988064209675766035584463299236235
06494317520722425405499266736358111222092353075238943051957607
72838177133711938809223918443876724379628144541547953255275703
55545843143202611749143674603115027112767793615940083335822504
14001260300000139604098161722910625646686414595219516699059074
64124112599480274057376820125309201418774936670930722094112920
75668511384565582317364152493210500975624064036271597500904886
41493391778556544669856827168913235058037152190508905547682028
60172358074680448465215575045155812495385151214152726263391080
32505413436163412529544236195170662429539872646199926257967
e = 65537

20. Captured traffic (with wrong exponent e = 65539)
20
c' =
628936728EB827FFCA8EF47ED38DEA19BA5C2FFF3B00D34A59BA
49002E4143BE5F8992C4CF46AC6CDAFA969BB4EC07C58D757245
DAAA794F5B382302ED906324B3973D453A2F4495783BDD6989DC7
5C6E7C530979F1E5216734BF3FB3203AE1FD5631B0FE135BD259A
377763ED63F961C7598C5C4871B990F3230A7BBEE60129D1B2B64
0B3AE2C36DD5B76F66AC5B9AA99C48FDF31E608DE005719BEA2A
DD92D5754E7ECBDF39F9D204820EF97D473FA897860587AE4B0C
4DF01E98C7B501C4FE26A5A4624DF3648FBB0F7F61DC79DAFE1E
9881A9A27A66CE3BB4D92FC52DB790ACD48A5009325A79D157106
07B30B7BCC37E305132F6A9A2C3A56E0A5990854

21. Captured traffic (with correct exponent e = 65537)
21
c =
06DEC6DCE2726801CB815FFF5443960B7C11AB9E7
487F3E3B7D9613979AC473E238AE4D5624F4B97F7
567D495D5871A1D1B234E42771FCF9B47EF43F85A
08299BC98D5A9AD16A6B102FC9EC03AACC01B526
79E089589D2CBB09E9F127A1829DC59AFC7197431
E59F1B63DAC08878D0F8D0C2885CE30E955334D63
C4C30D8A619EE245A584F4704A989B2992257AE29
503EDE0C5637DA220522ECB495AAA980103505459
AE36952052B4CF5EFEB2D847405C02A60AB2EAB92
8206BA0DFE8438C491264F19C93819E158A26F8507
A1083B7A223B1A6EA145EEC2B4084E87D094426F2
6D00C84FA24369C159EF5C029918118E784A101AB
D00A7B3B59E6C7E643BE

22. Demo client to break Raw RSA (2048-bit modulus)
22
$ java RSA_MiTM $n 65537 65539 $c $c_err
Hi, How are you?
The attacker recovered the secret
from <c, c', e, e'>

23. Conclusion/Discussion
23
● The main goal was to experiment with an incorrect RSA usage pattern
● That is, without integrity checks or digital signature
● The Man-in-the-middle (MiTM) just has to edit the public exponent e
● MiTM was able to recover plaintexts using Extended Euclidean Algo.
● Note that this attack works when RSA is used without any padding
● RSA without integrity checks can lead to interesting attacks
● In TLS, the server’s public key is digitallly signed, so MiTM’s job is very difficult to edit e
● RSA is a classical crypto system but has to be used very carefully

24. References
● W. Diffie and M. E. Hellman, “New Directions in Cryptography,” IEEE
Transactions on Information Theory, vol. IT-22, no. 6, November, 1976.
● R. L. Rivest, A. Shamir, and L. Adleman, “A method for obtaining digital
signatures and public-key cryptosystems,” CACM 21, 2, February, 1978.
● A. Menezes, P. van Oorschot, and S. Vanstone, “Handbook of Applied
Cryptography,” CRC Press, 1996.
● C. Paar and J. Pelzl, “Understanding Cryptography: A Textbook for Students
and Practitioners,” Springer, 2011.
24