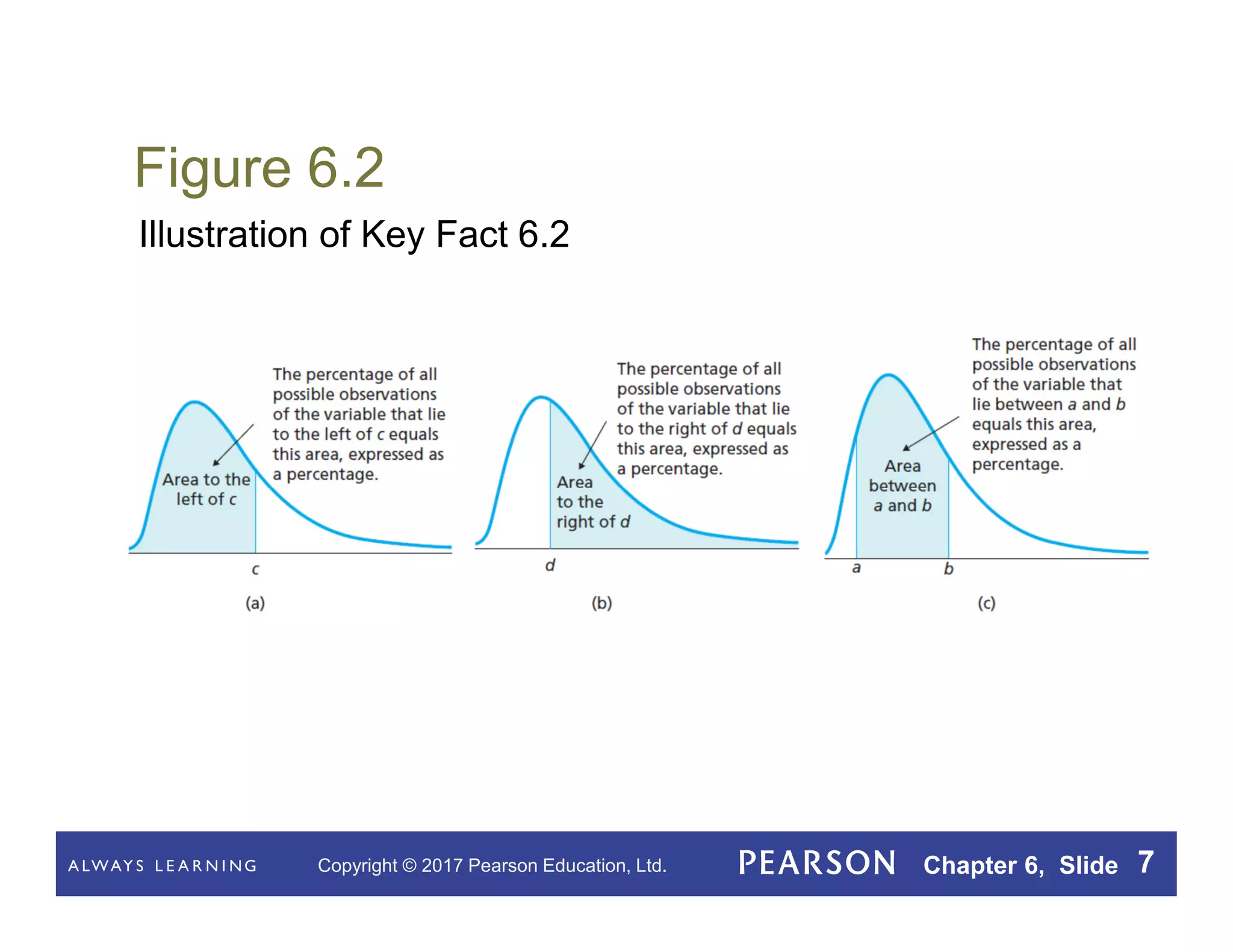
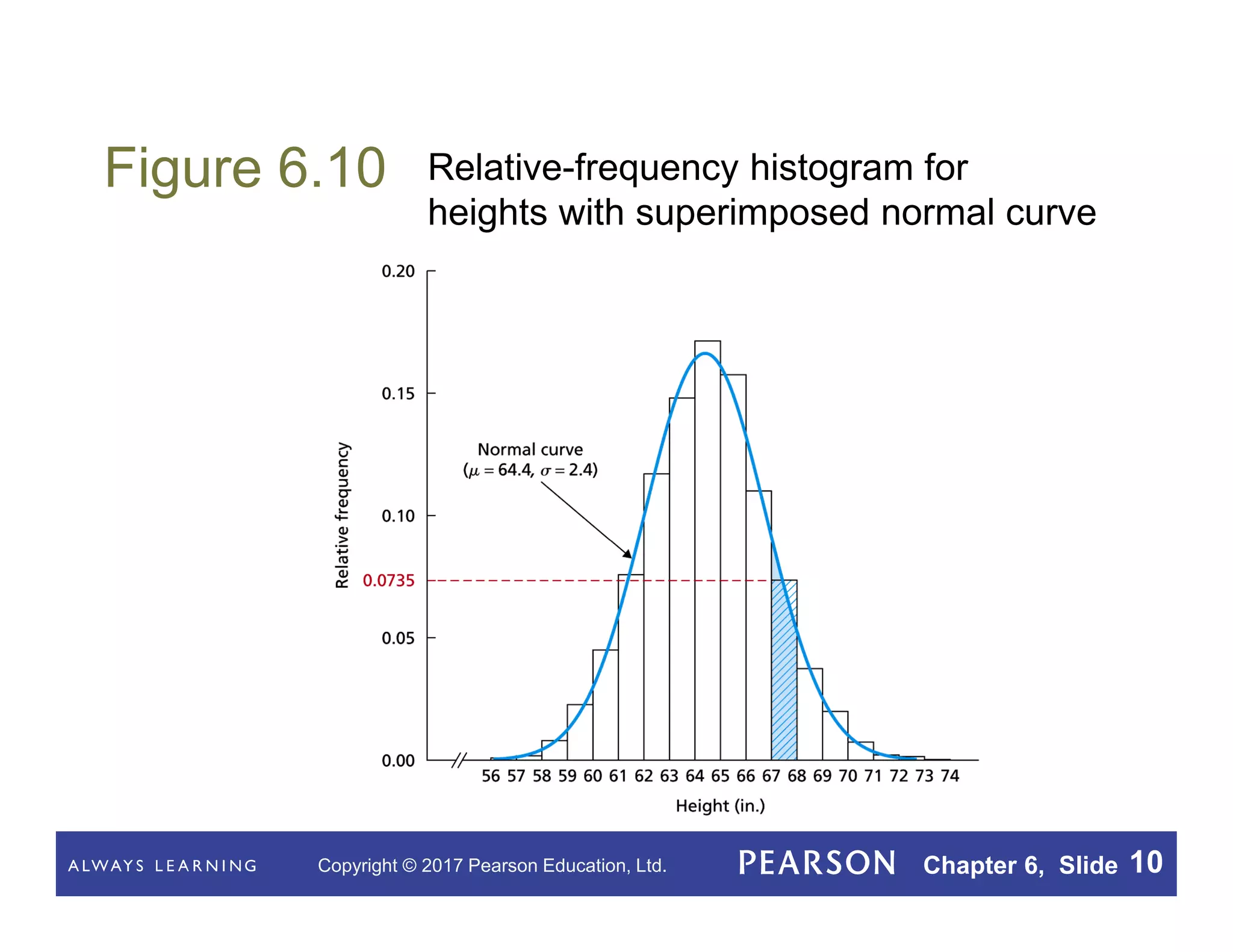
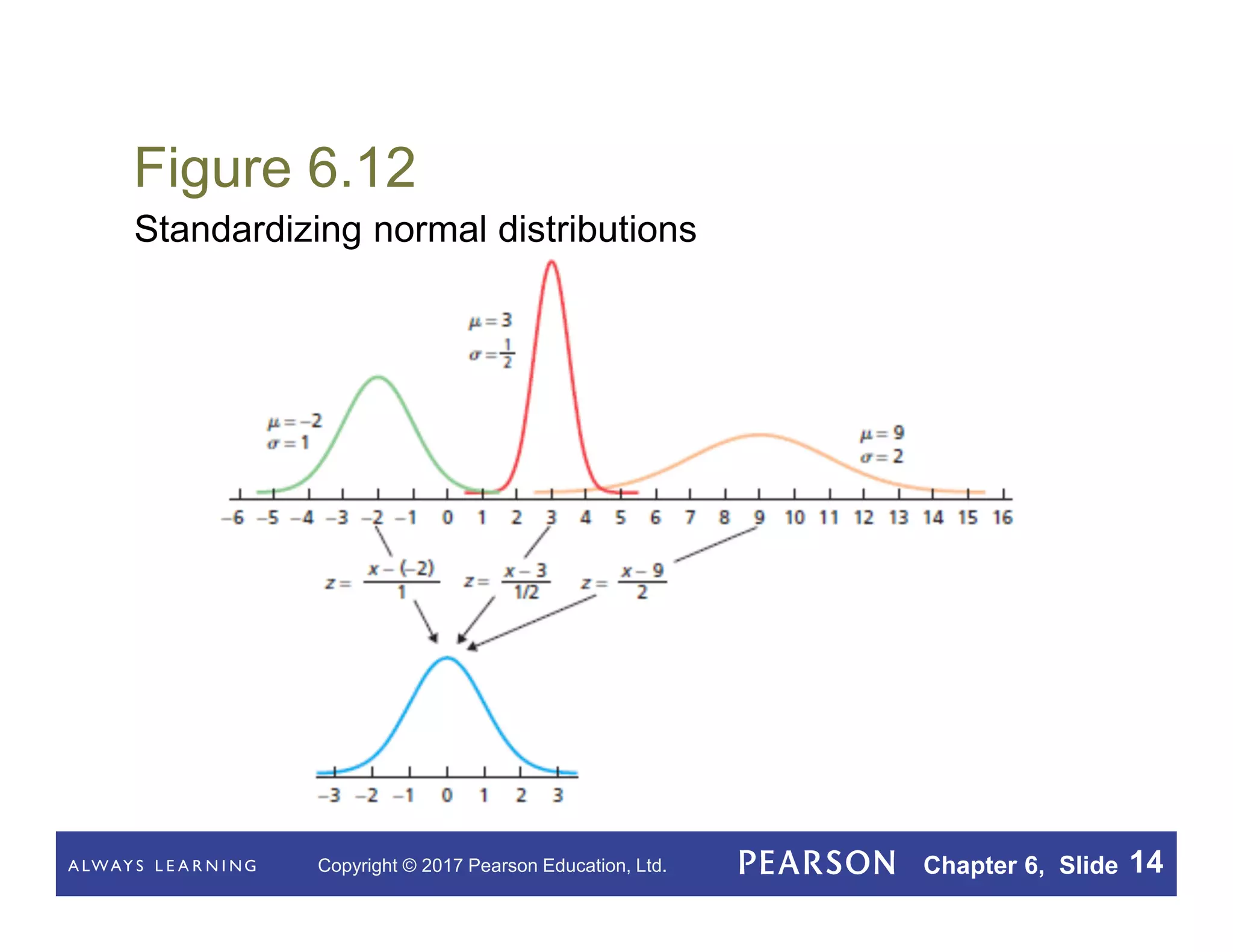
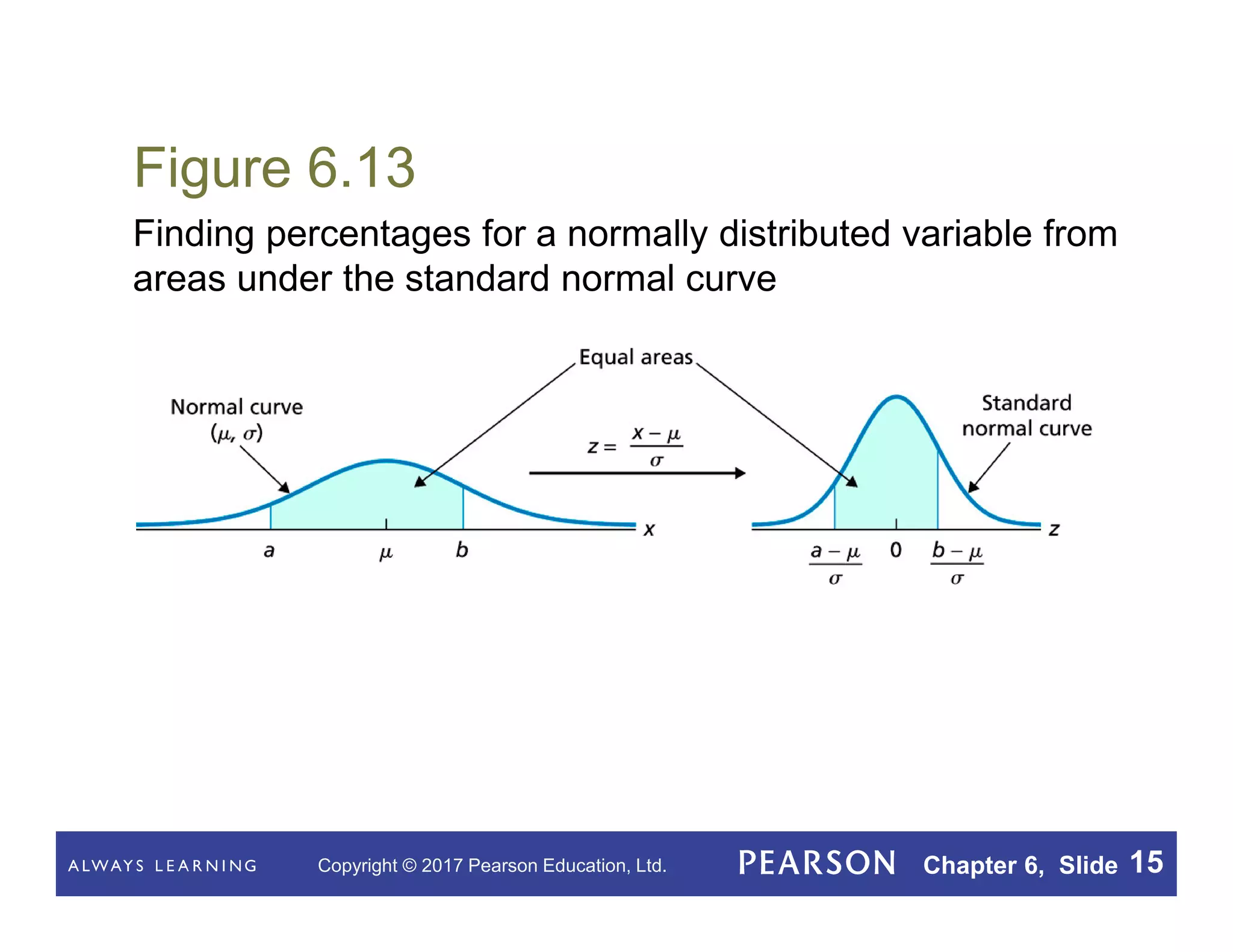
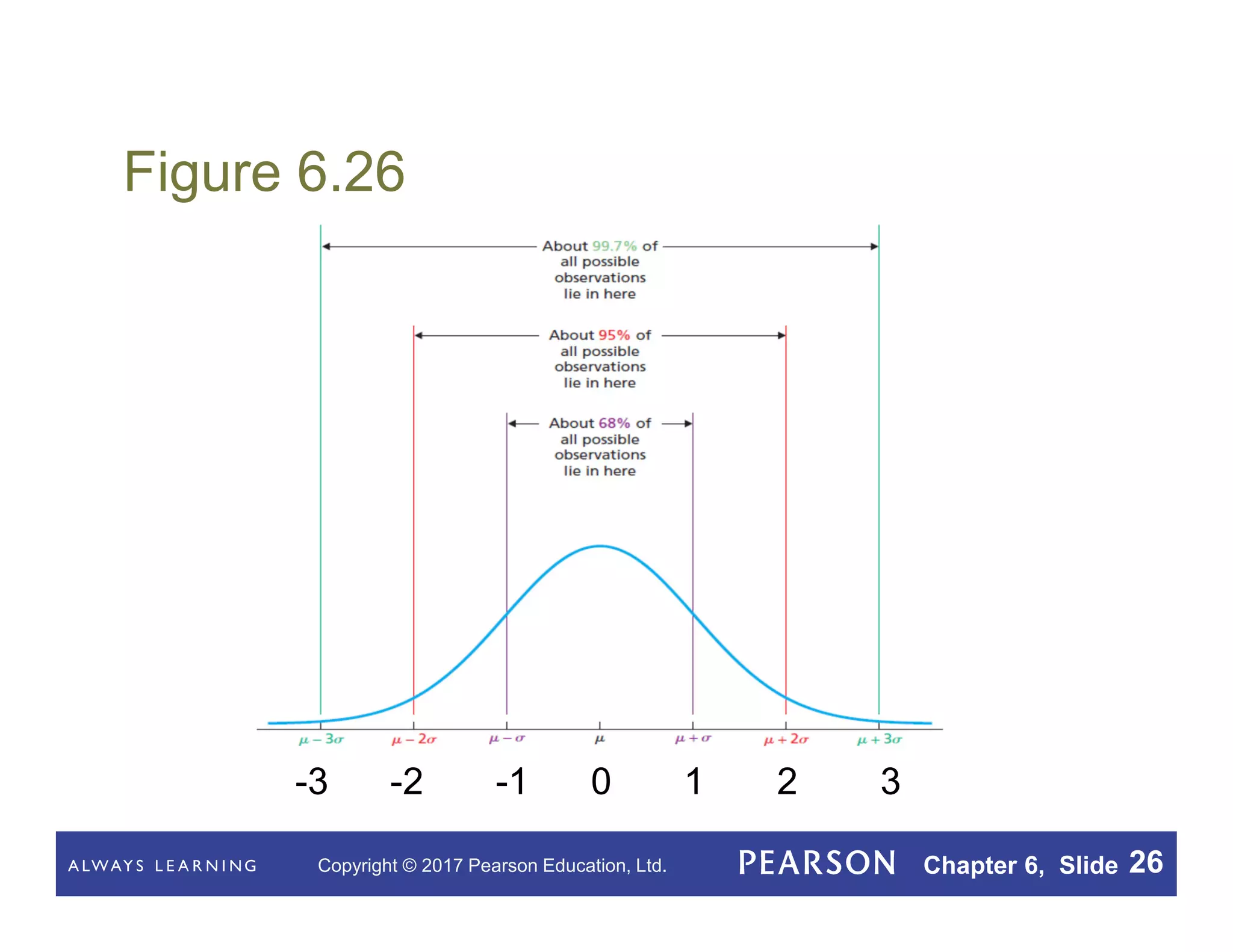
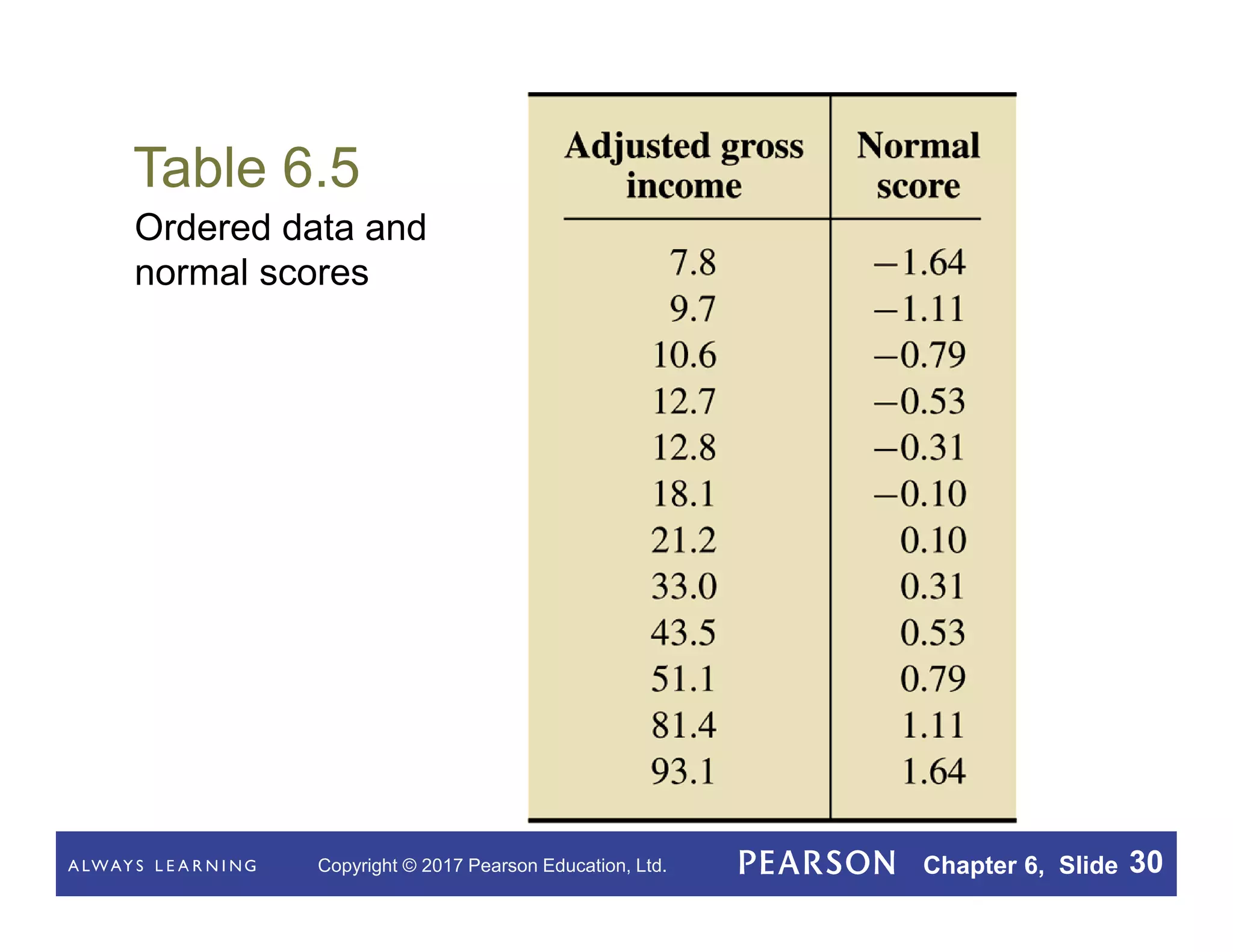
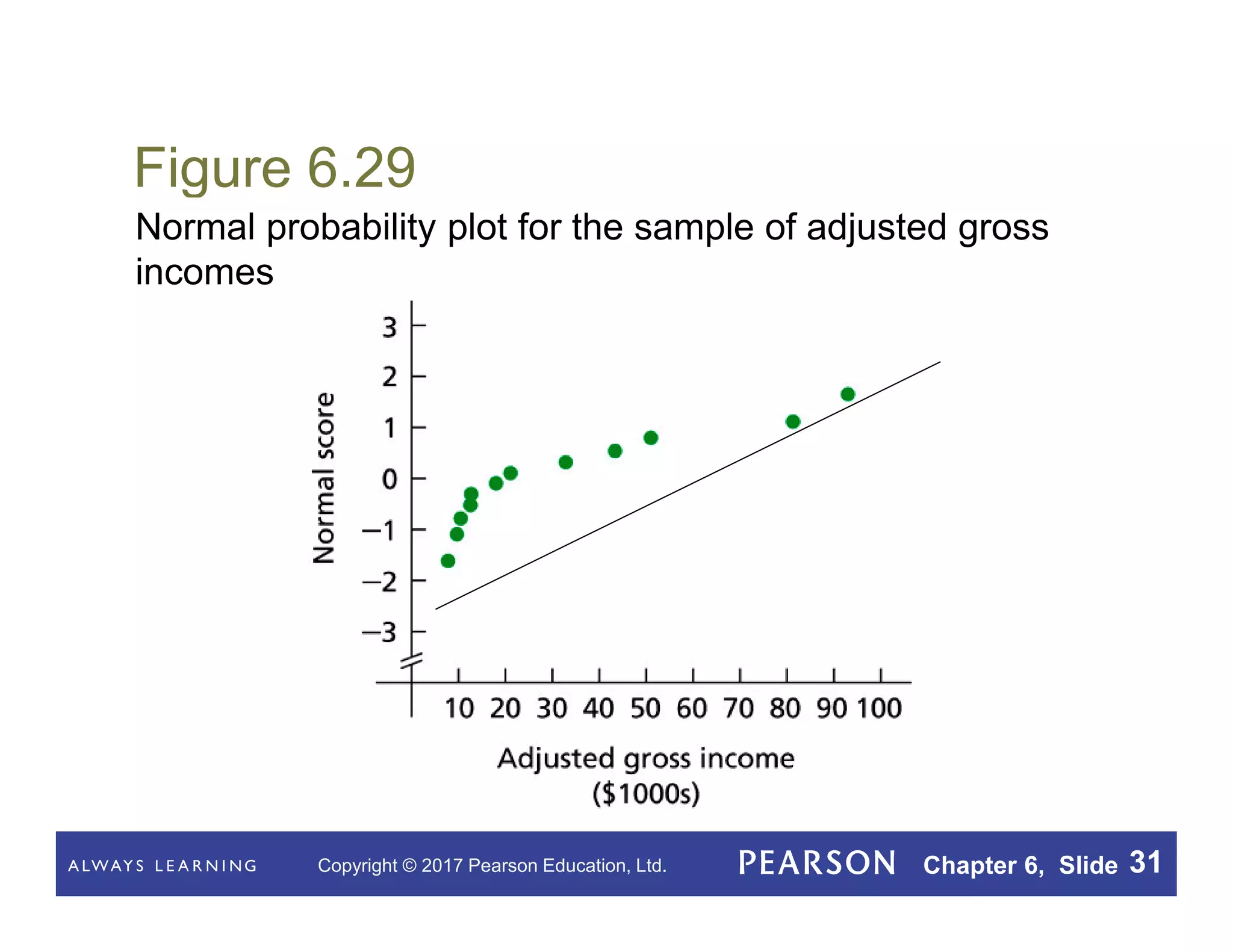
This document summarizes key concepts from Chapter 6 of a statistics textbook on the normal distribution. It introduces the normal distribution and its properties, including that a normal density curve has an area of 1 and the percentage of observations within a range equals the area under the curve. It defines a normally distributed variable as having a normal distribution shape and discusses standardizing normal distributions. Various procedures and facts are presented for working with normal distributions, including finding percentages of observations using the standard normal curve and assessing normality with normal probability plots.