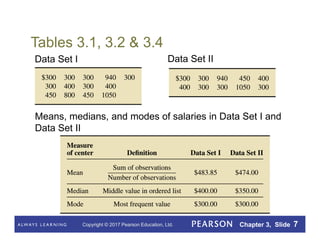
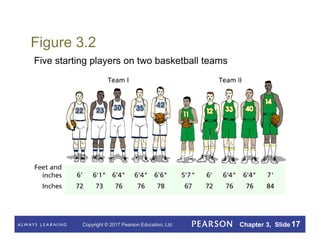
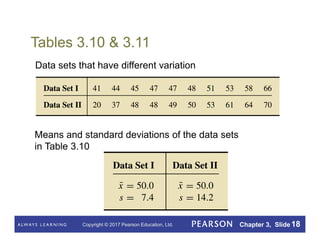
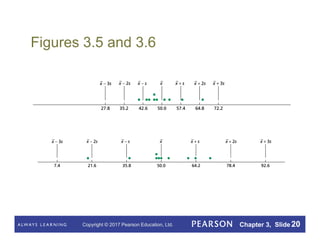
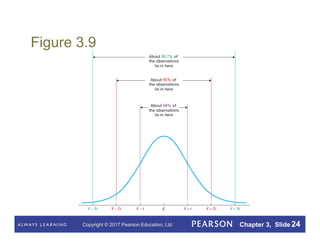
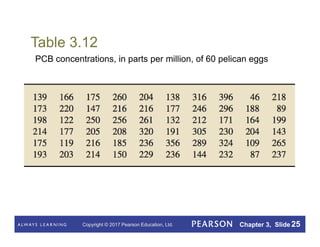
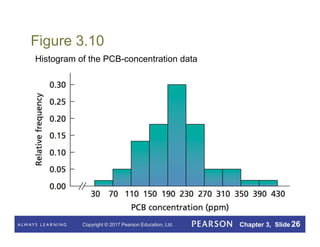
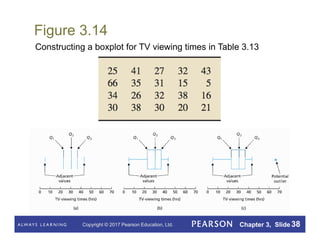
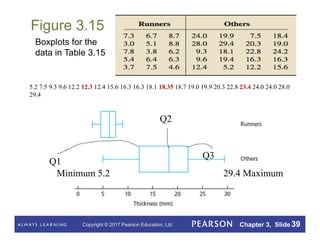
This document summarizes key concepts from Chapter 3 of a statistics textbook. It introduces descriptive measures such as the mean, median, mode, range, and standard deviation that are used to describe the center and variation of data sets. It also discusses the empirical rule and five-number summary, and how descriptive measures can be calculated for populations or estimated from samples. Boxplots are presented as a way to visually summarize and compare data sets.