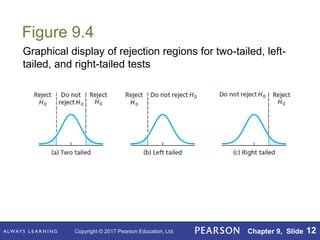
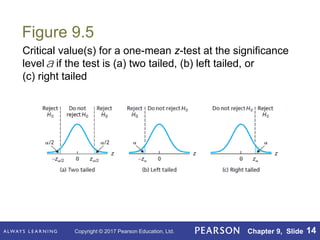
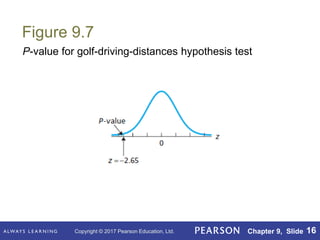
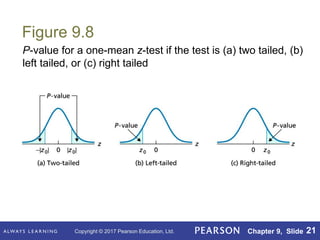
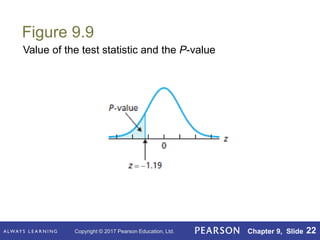
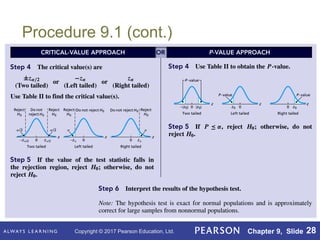
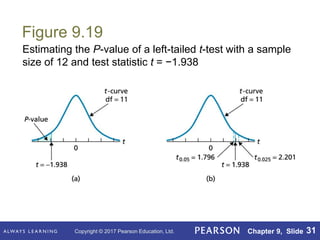
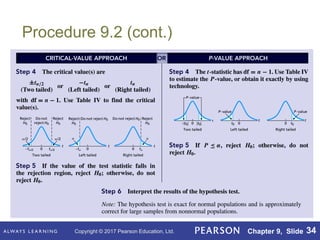
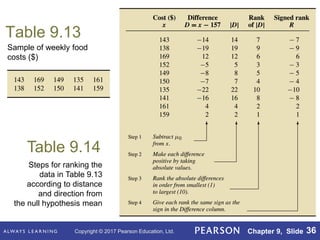
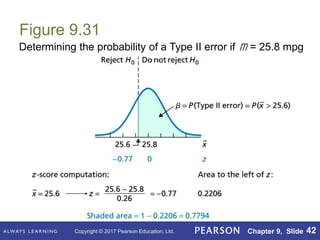
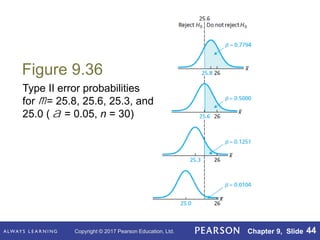
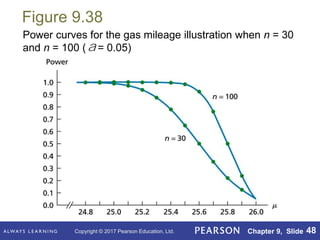
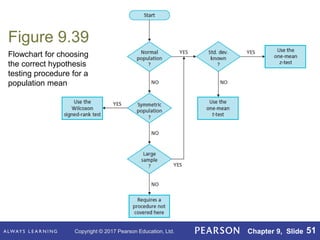
This document outlines key concepts in hypothesis testing for a single population mean from a statistics textbook. It introduces the null and alternative hypotheses, Type I and Type II errors, significance levels, and the critical value and p-value approaches. Specific hypothesis tests covered include the one-sample z-test, t-test, and Wilcoxon signed-rank test. It also discusses factors such as sample size that influence the power of a test and the probability of making a Type II error.