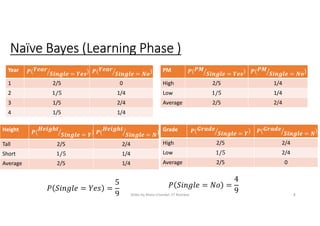
The document provides an overview of Bayesian classification and the Naive Bayes algorithm. It discusses how Thomas Bayes formulated Bayes' theorem and how the Naive Bayes classifier works by making the assumption that features are independent. The document explains the learning and testing phases of the Naive Bayes algorithm using examples, including how to handle continuous valued features. It also notes some issues like violating the independence assumption and how to prevent underflow problems in implementations.

1. Bayesian Classification
Thomas Bayes (1701 – 7 April 1761) was an English
statistician, philosopher and Presbyterian minister
who is known for having formulated a specific case of
the theorem that bears his name: Bayes' theorem.
Bayes never published what would eventually
become his most famous accomplishment, his notes
were edited and published after his death by Richard
Price
Sir Thomas Bayes
Slides by Manu Chandel, IIT Roorkee 1

2. Bayes Theorem
Total Probability
Bayes Theorem
E1 E2 E3 …………………………… EN
A
1. A is a outcome which can result from
all the events E1, E2, ………… EN
2. All the events E1, E2, E3………. EN are
mutually exclusive and exhaustive
Slides by Manu Chandel, IIT Roorkee 2

3. Bayes Theorem Example
Q. Given two bags each one having red and white balls.
Both bags have equal chance of being chosen.
If a ball is picked at random and found to be Red,
what is the probability that the ball was chosen from bag A?
Ans. Total probability of Red Ball =
=
=
Probability that red ball was from Bag A
∗
( )
=
Slides by Manu Chandel, IIT Roorkee 3

4. Discriminative v/s Generative classifiers
For a prediction function
Discriminative classifiers
estimate directly from
the training data
Generative classifiers estimate
and directly
from the training data.
Naïve Bayes Classifier is a generative classifier
Slides by Manu Chandel, IIT Roorkee 4

5. MAP Classification Rule
Maximum A Posterior rule says that :
“Jiski lathi uski bhains “
Input data belongs to the class whose is highest.
Example :
Suppose a news article is to be classified into following three categories: a) Politics b) Finance and
c) Sports.
So, X is our news article and three categories are denoted by Y1, Y2 and Y3 .
Lets say , ,
then according to MAP classification rule news article will be classified into category 2 i.e. finance.
Slides by Manu Chandel, IIT Roorkee 5

6. Naïve Bayes (Discrete values)
An input to the classifier is often a feature vector containing various feature values
e.g. A news article input to a news article classifier may be a vector of words.
In Bayes classification we need to learn and from the given data.
Here is feature vector with as feature values.
Learning joint probability ( , ,…… , )
is difficult. Hence Naïve Bayes
assumes that features are independent of each other. Assuming
independence of features leads to
( , ,…… , )
Slides by Manu Chandel, IIT Roorkee 6

7. Naïve Bayes Algorithm (with Example)
Learning phase of Naïve Bayes is represented by an example.
Classifier needs to learn and for all Y
Sr Year Height Pocket
Money
Grade Single
1 1 Average Low High Yes
2 2 Tall Average Low No
3 3 Short High High No
4 4 Average Average Low No
5 2 Tall High Low Yes
6 3 Tall Low High No
7 3 Average High Average Yes
8 1 Tall Average Average Yes
9 4 Short Average High Yes
Data collected
anonymously
from BTECH
Students IITR.
Slides by Manu Chandel, IIT Roorkee 7

8. Naïve Bayes (Learning Phase )
Year ( = ) ( = )
1 2/5 0
2 1/5 1/4
3 1/5 2/4
4 1/5 1/4
Height ( = ) ( = )
Tall 2/5 2/4
Short 1/5 1/4
Average 2/5 1/4
PM ( = ) ( = )
High 2/5 1/4
Low 1/5 1/4
Average 2/5 2/4
Grade ( = ) ( = )
High 2/5 2/4
Low 1/5 2/4
Average 2/5 0
Slides by Manu Chandel, IIT Roorkee 8

9. Naïve Bayes (Testing Phase)
What will be the outcome of X= <4,Tall,Average,High> ?
=
= 4
∗
=
∗
=
∗
=
∗ ( = )
= 1/5 * 2/5 * 2/5 * 2/5*5/9
= 0.00711
=
= 4
∗
=
∗
=
∗
=
∗ ( = )
= 1/4 * 2/4 * 2/4 * 2/4*4/9
= 0.0138 As 0.0138 > 0.00711 then X will be classified as Single = No
Slides by Manu Chandel, IIT Roorkee 9

10. Naïve Bayes (Continuous Values )
Conditional probability often modeled with the normal distribution
= =
1
2
exp(−
( − )
2
)
= mean of feature values of =
= standard deviation of feature values of =
Learning Phase
For = , , … … , = , , … . output Normal distributions.
Test Phase
Given an unknown instance = , , … . . ,
• Instead of looking-up tables, calculate conditional probabilities with all the normal distributions achieved in
the learning phrase
• Apply the MAP rule to make a decision
Slides by Manu Chandel, IIT Roorkee 10

11. Naïve Bayes Continuous Value Example
• Temperature is naturally of continuous value.
• Yes: 25.2, 19.3, 18.5, 21.7, 20.1, 24.3, 22.8, 23.1, 19.8
• No: 27.3, 30.1, 17.4, 29.5, 15.1
• Estimate mean and variance for each class
• and
•
• Learning phase output two Gaussian models for
•
.
( . )
.
•
.
( . )
.
Slides by Manu Chandel, IIT Roorkee 11

12. Relevant Issues
1. Violation of independence Assumption
2. Zero Conditional Probability Problem
If no example contains a feature value In this circumstances
This can be solved by
Slides by Manu Chandel, IIT Roorkee 12

13. Underflow Prevention
• Multiplying lots of probabilities, which are between 0 and 1 by definition, can
result in floating-point underflow.
• Since it is better to perform all computations by
summing logs of probabilities rather than multiplying probabilities.
• Class with highest final un-normalized log probability score is still the most
probable.
Slides by Manu Chandel, IIT Roorkee 13

14. Summary
• Naïve Bayes: the conditional independence assumption
• Training is very easy and fast, just requiring considering each attribute in each class separately.
• Test is straightforward, just looking up tables or calculating conditional probabilities with
estimated distributions.
• A popular generative model
• Performance competitive to most of state-of-the-art classifiers even in presence of violating
independence assumption.
• Many successful applications, e.g., spam mail filtering
Slides by Manu Chandel, IIT Roorkee 14