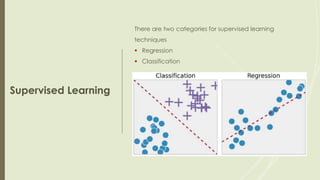
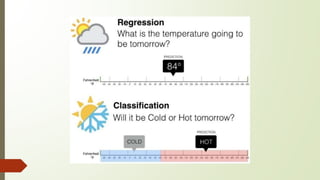
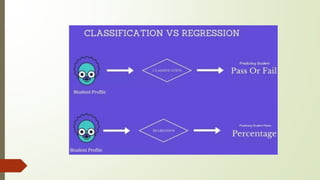
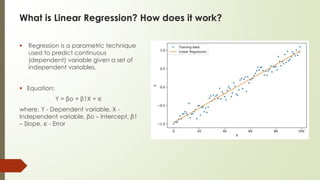
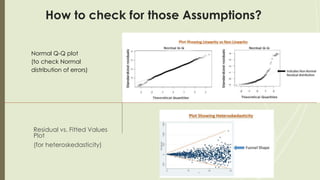
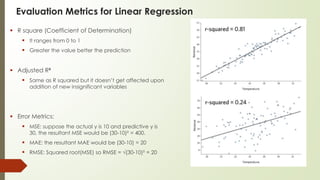
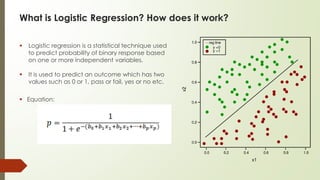
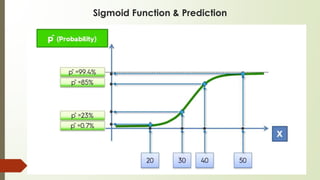
Supervised machine learning involves regression and classification techniques. Linear regression predicts continuous output values based on linear relationships between input features. It assumes features are linearly related and errors are normally distributed. Logistic regression predicts binary classification with probabilities calculated from the sigmoid function. It is used for problems like predicting clicks from user data. Both techniques are evaluated using metrics like R-squared and accuracy derived from confusion matrices. Case studies demonstrate using linear regression to predict ice cream revenue from temperature, and logistic regression to classify customer ad clicks.

1. Supervised Machine
Learning
By Rahul Pal
Lead Data Scientist

2. Agenda
 Introduction to Machine Learning
 Introduction to Supervised Learning
 Classification vs Regression
 Introduction to Linear Regression
 Learning of Linear Regression
 Introduction to Logistic Regression
 Learning to Logistic Regression
 Case Studies

3. `
Introduction to
Machine Learning
Machine learning is the subfield of
computer science that gives
computer the ability to learn
without being programmed

4. Practical Examples

5. Types of ML
techniques
1. Supervised Learning
2. Unsupervised Learning
3. Reinforcement Learning

6. Supervised Learning
There are two categories for supervised learning
techniques
 Regression
 Classification

9. Regression
 Linear Regression
 Multi-Linear Regression
 Polynomial Regression
 Decision Tree Regression
 Random Forest Regression

10. Linear Regression

11. What is Linear Regression? How does it work?
 Regression is a parametric technique
used to predict continuous
(dependent) variable given a set of
independent variables.
 Equation:
Y = βo + β1X + ∈
where, Y - Dependent variable, X -
Independent variable, βo – Intercept, β1
– Slope, ∈ - Error

12. What are the
assumptions made
in Linear regression?
1. There exists a linear and additive relationship
between dependent (DV) and independent
variables (IV)
2. There must be no correlation among independent
variables (no multicollinearity
3. The error terms must possess constant variance (no
heteroskedasticity)
4. No autocorrelation
5. The dependent variable and the error terms
must possess a normal distribution.

13. How to check for those Assumptions?
Normal Q-Q plot
(to check Normal
distribution of errors)
Residual vs. Fitted Values
Plot
(for heteroskedasticity)

14. Other tests:
1. Durbin Watson Statistic (DW) - Autocorrelation
2. Variance Inflation Factor (VIF) – Multicollinearity
3. Breusch-Pagan/Cook Weisberg Test – Heteroskedasticity

15. Evaluation Metrics for Linear Regression
 R square (Coefficient of Determination)
 It ranges from 0 to 1
 Greater the value better the prediction
 Adjusted R²
 Same as R squared but it doesn’t get affected upon
addition of new insignificant variables
 Error Metrics:
 MSE: suppose the actual y is 10 and predictive y is
30, the resultant MSE would be (30-10)² = 400.
 MAE: the resultant MAE would be (30-10) = 20
 RMSE: Squared root(MSE) so RMSE = √(30-10)² = 20

16. Regression
Case Study
You own an ice cream business and you would like to create a
model that could predict the daily revenue in dollars based on
the outside air temperature (°C).
You decided that a Linear Regression model might be a good
candidate to solve this problem.
Data set:
Independent variable X: Outside Air Temperature
Dependent variable Y: Overall daily revenue generated in dollars

17. Logistic Regression

18. What is Logistic Regression? How does it work?
 Logistic regression is a statistical technique used
to predict probability of binary response based
on one or more independent variables.
 It is used to predict an outcome which has two
values such as 0 or 1, pass or fail, yes or no etc.
 Equation:

19. Sigmoid Function & Prediction

20. Evaluation Metrics for Logistic Regression
 Confusion Matrix (in fig): It can also be used to
derive
 Accuracy : (TP+TN) / (TP+TN+TF+FP)
 Precision : (TP) / (TP+FP)
 Recall : (TP) / (TP+FN)
 F-1 Score : 2*(Precision*Recall) / (Precision+Recall)
 Other metrics:
 Receiver Operator Characteristic (ROC)
 Akaike Information Criteria (AIC)

21. Classification
Case Study
You own a advertisement agency. You have customer data who
watches your ads and clicks on it or not. On the basis of this data
you want to try enhancing your customer targeting.
You wanted to categorize your customers into those who will
click on ad vs those who won’t. So we will build a logistic model
to achieve this goal and maximize our click conversion rate.
Data set:
Independent variable X: Customer Related Data
Dependent variable Y: Clicked on Ad

22. “
”
Thank You.
Feel free to contact for any queries
Rahul Pal
the.rahul.pal@gmail.com