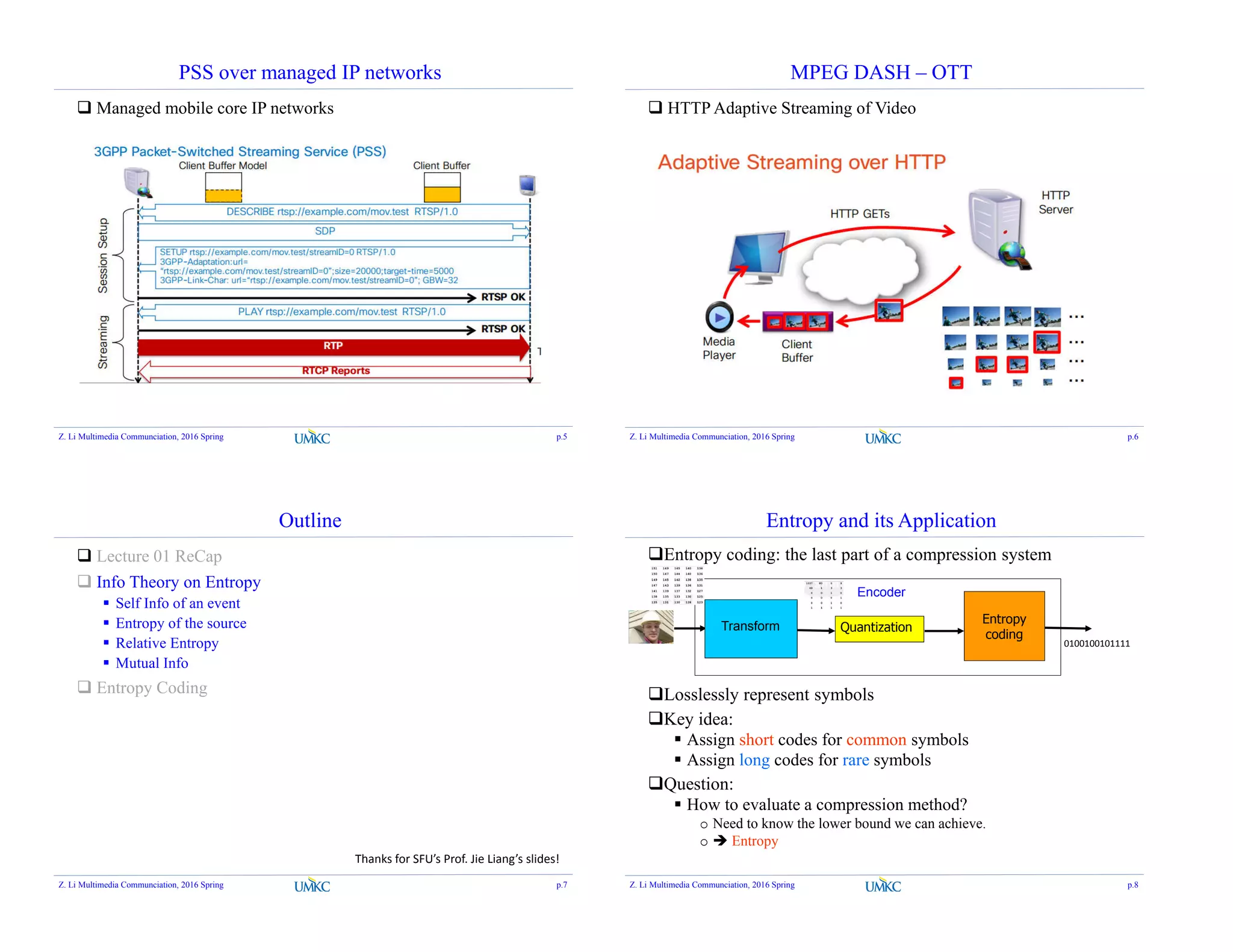
The document outlines a lecture on entropy and lossless coding, emphasizing information theory and its applications in multimedia communication. It discusses key concepts such as self-information, joint entropy, and conditional entropy, along with the historical background of Claude Shannon's work. Additionally, it introduces various entropy-related formulas and examples relevant to video coding standards and compression methods.

![Claude Shannon: 1916-2001
A distant relative of Thomas Edison
1932: Went to University of Michigan.
1937: Master thesis at MIT became the foundation of
digital circuit design:
o “The most important, and also the most famous,
master's thesis of the century“
1940: PhD, MIT
1940-1956: Bell Lab (back to MIT after that)
1948: The birth of Information Theory
o A mathematical theory of communication, Bell System
Technical Journal.
Z. Li Multimedia Communciation, 2016 Spring p.9
Axiom Definition of Information
Information is a measure of uncertainty or surprise
Axiom 1:
Information of an event is a function of its probability:
i(A) = f (P(A)). What’s the expression of f()?
Axiom 2:
Rare events have high information content
Water found on Mars!!!
Common events have low information content
It’s raining in Vancouver.
Information should be a decreasing function of the probability:
Still numerous choices of f().
Axiom 3:
Information of two independent events = sum of individual information:
If P(AB)=P(A)P(B) i(AB) = i(A) + i(B).
Only the logarithmic function satisfies these conditions.
Z. Li Multimedia Communciation, 2016 Spring p.10
Self-information
)(log
)(
1
log)( xp
xp
xi bb
• Shannon’s Definition [1948]:
• X: discrete random variable with alphabet {A1, A2, …, AN}
• Probability mass function: p(x) = Pr{ X = x}
• Self-information of an event X = x:
If b = 2, unit of information is bit
Self information indicates the number of bits
needed to represent an event.
1
P(x)
)(log xPb
0
Z. Li Multimedia Communciation, 2016 Spring p.11
Recall: the mean of a function g(X):
Entropy is the expected self-information of the r.v. X:
The entropy represents the minimal number of bits needed to
losslessly represent one output of the source.
Entropy of a Random Variable
x xp
xpXH
)(
1
log)()(
)g()())(()( xxpXgE xp
)(log
)(
1
log )()( XpE
Xp
EH xpxp
Also write as H (p): function of the distribution of X, not the value of X.
Z. Li Multimedia Communciation, 2016 Spring p.12](https://image.slidesharecdn.com/lec02-160217035135/75/Multimedia-Communication-Lec02-Info-Theory-and-Entropy-3-2048.jpg)

![Conditional Entropy
Example: for the following joint distribution p(x, y), find H(Y |
X).
1 2 3 4
1 1/8 1/16 1/32 1/32
2 1/16 1/8 1/32 1/32
3 1/16 1/16 1/16 1/16
4 1/4 0 0 0
Y
X
( | ) ( ) ( | )log( ( | )) ( , )log( ( | ))
x y x y
H Y X p x p y x p y x p x y p y x
Need to find conditional prob p(y | x)
( , )
( | )
( )
p x y
p y x
p x
Need to find marginal prob p(x) first (sum columns).
P(X): [ ½, ¼, 1/8, 1/8 ] >> H(X) = 7/4 bits
P(Y): [ ¼ , ¼, ¼, ¼ ] >> H(Y) = 2 bits
H(X|Y) = ∑ = ( | = )
= ¼ H(1/2 ¼ 1/8 1/8 )
+ 1/4H(1/4, ½, 1/8 ,1/8)
+ 1/4H(1/4 ¼ ¼ ¼ ) +
1/4H(1 0 0 0)
= 11/8 bits
Z. Li Multimedia Communciation, 2016 Spring p.17
Chain Rule
H(X, Y) = H(X) + H(Y|X) = H(Y) + H(X|Y)
Proof:
H(X) H(Y)
H(X | Y) H(Y | X)
Total area: H(X, Y)
x
x yx y
x y
x y
XYHXHXYHxpxp
xypyxpxpyxp
xypxpyxp
yxpyxpYXH
).|()()|()(log)(
)|(log),()(log),(
)|()(log),(
),(log),(),(
Simpler notation:
)|()(
))|(log)((log)),((log),(
XYHXH
XYpXpEYXpEYXH
Z. Li Multimedia Communciation, 2016 Spring p.18
Conditional Entropy
Example: for the following joint distribution p(x, y), find H(Y |
X).
Indeed, H(X|Y) = H(X, Y) – H(Y)= 27/8 – 2 = 11/8 bits
1 2 3 4
1 1/8 1/16 1/32 1/32
2 1/16 1/8 1/32 1/32
3 1/16 1/16 1/16 1/16
4 1/4 0 0 0
Y
X
P(X): [ ½, ¼, 1/8, 1/8 ] >> H(X) = 7/4 bits
P(Y): [ ¼ , ¼, ¼, ¼ ] >> H(Y) = 2 bits
H(X|Y) = ∑ = ( | = )
= ¼ H(1/2 ¼ 1/8 1/8 )
+ 1/4H(1/4, ½, 1/8 ,1/8)
+ 1/4H(1/4 ¼ ¼ ¼ ) +
1/4H(1 0 0 0)
= 11/8 bits
Z. Li Multimedia Communciation, 2016 Spring p.19
Chain Rule
H(X,Y) = H(X) + H(Y|X)
Corollary: H(X, Y | Z) = H(X | Z) + H(Y | X, Z)
Note that: ( , | ) ( | , ) ( | )p x y z p y x z p x z
(Multiply by p(z) at both sides, we get )( , , ) ( | , ) ( , )p x y z p y x z p x z
))|,((log)|,(log),,(
)|,(log)|,()()|,(
ZYXpEzyxpzyxp
zyxpzyxpzpZYXH
x y z
x yz
Proof:
),|()|(
)),|((log))|((log)|,(
ZXYHZXH
ZXYpEZXpEZYXH
Z. Li Multimedia Communciation, 2016 Spring p.20](https://image.slidesharecdn.com/lec02-160217035135/75/Multimedia-Communication-Lec02-Info-Theory-and-Entropy-5-2048.jpg)



![Carter-Gill’s Conjecture [1974]
Carter-Gill’s Conjecture [1974]
Every uniquely decodable code can be replaced by a prefix-free code
with the same set of codeword compositions.
So we only need to study prefix-free code.
Z. Li Multimedia Communciation, 2016 Spring p.37
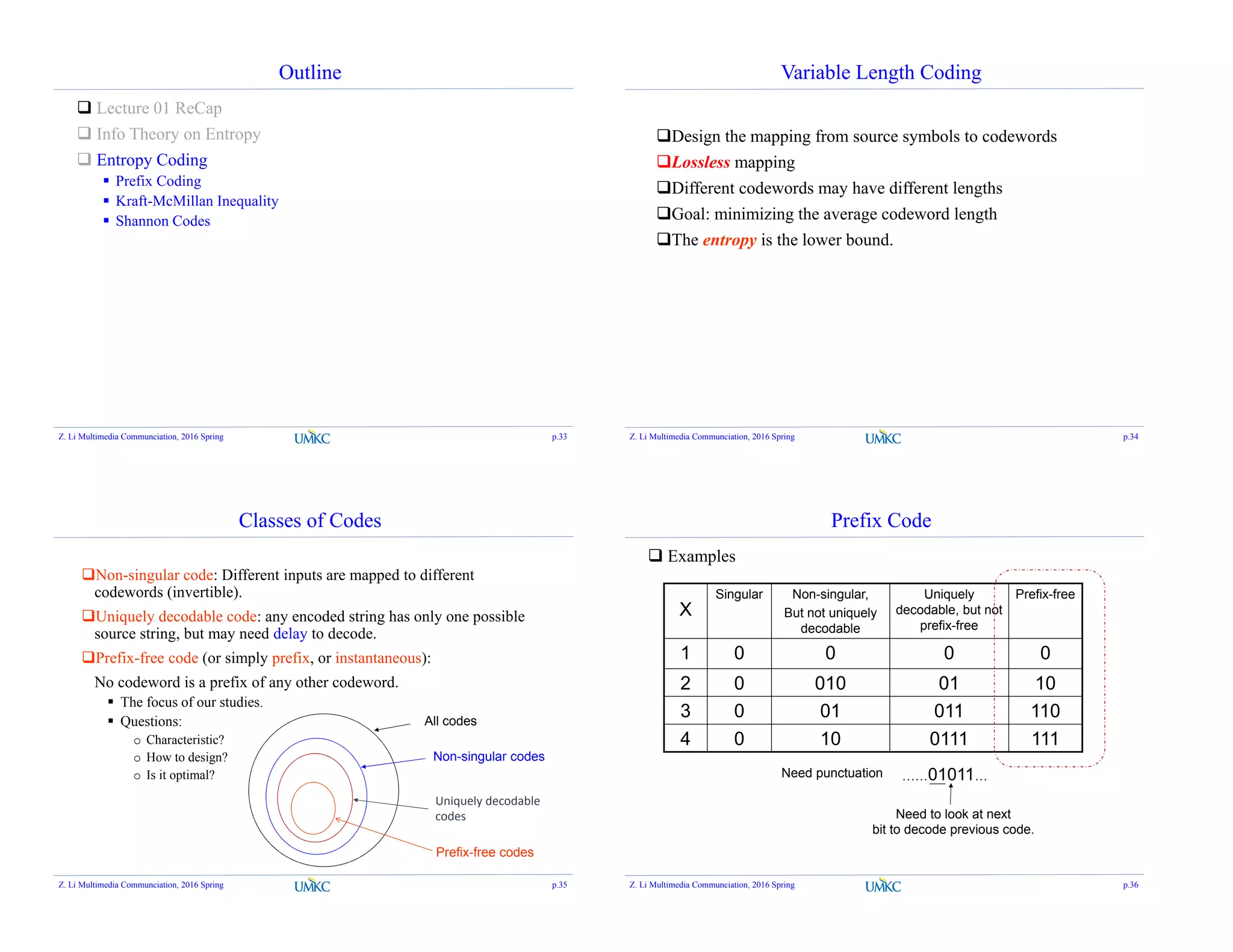
Prefix-free Code
Can be uniquely decoded.
No codeword is a prefix of another one.
Also called prefix code
Goal: construct prefix code with minimal expected length.
Can put all codewords in a binary tree:
0 1
0 1
0 1
0
10
110 111
Root node
leaf node
Internal node
Prefix-free code contains leaves only.
How to express the requirement mathematically?
Z. Li Multimedia Communciation, 2016 Spring p.38
Kraft-McMillan Inequality
12
1
N
i
li
• The codeword lengths li, i=1,…N of a prefix code over an
alphabet of size D(=2) satisfies the inequality
Conversely, if a set of {li} satisfies the inequality
above, then there exists a prefix code with codeword
lengths li, i=1,…N.
The characteristic of prefix-free codes:
Z. Li Multimedia Communciation, 2016 Spring p.39
Kraft-McMillan Inequality
2212
11
L
N
i
lL
N
i
l ii
Consider D=2: expand the binary code tree to full depth
L = max(li)
0
10
110
111
Number of nodes in the last level:
Each code corresponds to a sub-tree:
The number of off springs in the last level:
K-M inequality:
# of L-th level offsprings of all codes is less than 2^L !
ilL
2
L
2
L = 3
Example: {0, 10, 110, 111}
Z. Li Multimedia Communciation, 2016 Spring p.40
2^3=8
{4, 2, 0, 0}](https://image.slidesharecdn.com/lec02-160217035135/75/Multimedia-Communication-Lec02-Info-Theory-and-Entropy-10-2048.jpg)
![Kraft-McMillan Inequality
0
10
110 111
11
Invalid code: {0, 10, 11, 110, 111}
Leads to more than
2^L offspring: 12> 23
12
1
i
li
K-M inequality:
Z. Li Multimedia Communciation, 2016 Spring p.41
Extended Kraft Inequality
Countably infinite prefix code also satisfies the Kraft
inequality:
Has infinite number of codewords.
Example:
0, 10, 110, 1110, 11110, 111……10, ……
(Golomb-Rice code, next lecture)
Each codeword can be mapped to a subinterval in [0, 1] that is
disjoint with others (revisited in arithmetic coding)
1
1
i
li
D
)
0
)
10
)
0 0.5 0.75 0.875 1
110 ……
Z. Li Multimedia Communciation, 2016 Spring p.42
0
10
110
….
L = 3
Optimal Codes (Advanced Topic)
How to design the prefix code with the minimal expected
length?
Optimization Problem: find {li} to
1..
min
i
i
l
ii
l
Dts
lp
Lagrangian solution:
Ignore the integer codeword length constraint for now
Assume equality holds in the Kraft inequality
il
ii DlpJ Minimize
Z. Li Multimedia Communciation, 2016 Spring p.43
Optimal Codes
il
ii DlpJ
0lnLet
il
i
i
DDp
l
J
D
p
D ili
ln
1intongSubstituti il
D
Dln
1
i
l
pD i
or
iDi pl log-
*
The optimal codeword length is the self-information of an event.
Expected codeword length:
)(log*
XHpplpL DiDiii Entropy of X !
Z. Li Multimedia Communciation, 2016 Spring p.44](https://image.slidesharecdn.com/lec02-160217035135/75/Multimedia-Communication-Lec02-Info-Theory-and-Entropy-11-2048.jpg)

![Optimal Code
The optimal code with integer lengths should be better than
Shannon code
1)()( *
XHLXH DD
To reduce the overhead per symbol:
Encode a block of symbols {x1, x2, …, xn} together
),...,,(
1
),...,,(),...,,(
1
212121 nnnn xxxlE
n
xxxlxxxp
n
L
1),...,,(),...,,(),...,,( 212121 nnn XXXHxxxlEXXXH
Assume i.i.d. samples: )(),...,,( 21 XnHXXXH n
n
XHLXH n
1
)()( )(XHLn if stationary.
(entropy rate)
Z. Li Multimedia Communciation, 2016 Spring p.49
Optimal Code
Impact of wrong pdf: what’s the penalty if the pdf we use is different
from the true pdf?
True pdf: p(x) Codeword length: l(x)
Estimated pdf: q(x) Expected length: Epl(X)
1)||()()()||()( qpDpHXlEqpDpH p
Proof: assume Shannon code
)(
1
log)(
xq
xl
1
)(
1
log)(
)(
1
log)()(
xq
xp
xq
xpXlEp
1)||()(1
)(
1
)(
)(
log)(
qpDXH
xpxq
xp
xp
The lower bound is derived similarly.
Z. Li Multimedia Communciation, 2016 Spring p.50
Shannon Code is not optimal
Example:
Binary r.v. X: p(0)=0.9999, p(1)=0.0001.
Entropy: 0.0015 bits/sample
Assign binary codewords by Shannon code:
)(
1
log)(
xp
xl
.1
9999.0
1
log2
.14
0001.0
1
log2
Expected length: 0.9999 x 1+ 0.0001 x 14 = 1.0013.
Within the range of [H(X), H(X) + 1].
But we can easily beat this by the code {0, 1}
Expected length: 1.
Z. Li Multimedia Communciation, 2016 Spring p.51
Q&A
Z. Li Multimedia Communciation, 2016 Spring p.52](https://image.slidesharecdn.com/lec02-160217035135/75/Multimedia-Communication-Lec02-Info-Theory-and-Entropy-13-2048.jpg)