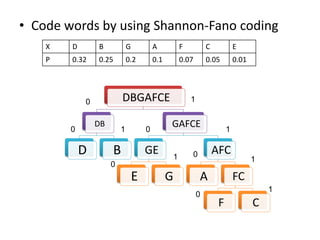
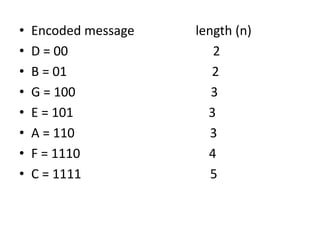
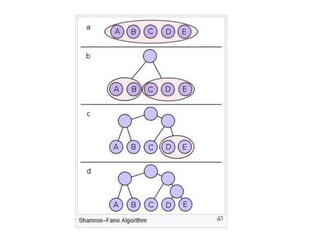
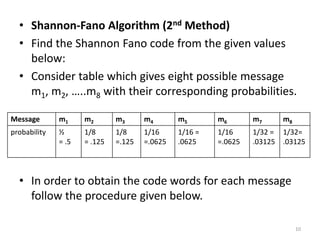
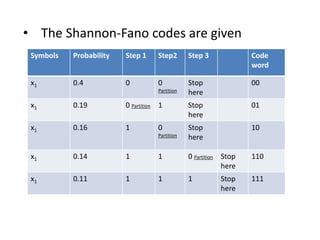
The document provides a detailed explanation of Shannon-Fano coding, a method for constructing prefix codes based on symbols and their probabilities, aimed at data compression. It outlines the algorithm for generating codes, including the process of sorting symbols, partitioning sets, and assigning binary digits. Additionally, it discusses calculating average codeword lengths and code efficiency, using various examples to illustrate the application of the Shannon-Fano method.

1. Introduction to Data communication
Topic : Shanon Fano Coding
Lecture #11
Dr Rajiv Srivastava
Director
Sagar Institute of Research & Technology (SIRT)
Sagar Group of Institutions, Bhopal
http://www.sirtbhopal.ac.in

2. Unit 1
Lecture 11
2

3. Shannon Fano Coding
• Its a method of constructing prefix code based on a set of
symbols and their probabilities estimated or measured.
• The technique was proposed in Shannon's "A Mathematical
Theory of Communication", his 1948 article introducing the
field of information theory.
• In the field of data compression, Shannon–Fano coding,
named after Claude Shannon and Robert Fano, is a technique
for constructing a prefix code based on a set of symbols and
their probabilities (estimated or measured). It is suboptimal in
the sense that it does not achieve the lowest possible
expected code word length like Huffman coding; however
unlike Huffman coding, it does guarantee that all code word
lengths are within one bit of their theoretical ideal .

4. Basic Technique
In Shannon–Fano coding, the symbols are arranged in order
from most probable to least probable, and then divided into
two sets whose total probabilities are as close as possible to
being equal.
All symbols then have the first digits of their codes assigned;
symbols in the first set receive "0" and symbols in the second
set receive "1".
As long as any sets with more than one member remain, the
same process is repeated on those sets, to determine
successive digits of their codes.
When a set has been reduced to one symbol this means the
symbol's code is complete and will not form the prefix of any
other symbol's code.

5. Shannon Fano Algorithm
A Shannon–Fano tree is built according to a specification
designed to define an effective code table. The actual
algorithm is simple:
1. For a given list of symbols, develop a corresponding list of
probabilities or frequency counts so that ea h s ol’s
relative frequency of occurrence is known.
2. Sort the lists of symbols according to frequency, with the
most frequently occurring symbols at the left and the least
common at the right.
3. Divide the list into two parts, with the total frequency
counts of the left part being as close to the total of the
right as possible.

6. 4. The left part of the list is assigned the binary
digit 0, and the right part is assigned the digit
1. This means that the codes for the symbols
in the first part will all start with 0, and the
codes in the second part will all start with 1.
5. Recursively apply the steps 3 and 4 to each of
the two halves, subdividing groups and
adding bits to the codes until each symbol
has become a corresponding code leaf on the
tree.

9. This is how the
average bits in a
symbol is
calculated.

10. • Shannon-Fano Algorithm (2nd Method)
• Find the Shannon Fano code from the given values
below:
• Consider table which gives eight possible message
m1, m2, ….. 8 with their corresponding probabilities.
• In order to obtain the code words for each message
follow the procedure given below.
10
Message m1 m2 m3 m4 m5 m6 m7 m8
probability ½
= .5
1/8
= .125
1/8
=.125
1/16
=.0625
1/16 =
.0625
1/16
=.0625
1/32 =
.03125
1/32=
.03125

11. • Procedure to obtain Shannon-Fano code:
• Step 1: list the source symbols (message) in the
order of decreasing probability.
• Step 2: partition the set of symbols into two sets
that are as close to being equiprobable as
possible.
• Step 3: Assign 0 to each message in the upper set
and 1 to each message in the lower set.
• Step 4: Continue this process, each time
partitioning the sets with as nearly equal
probabilities as possible until further partitioning
is not possible.
11

12. • By following this procedure we get the code
for each message as shown in table.
12
Message Probability Column I Column
II
Column
III
Column
IV
Column
V
Code word No. of bits
per code
word
m1 .5 0
Partition
Stop Here 0 1
m2 .125 1 0 0
Partition
Stop Here 100 3
m3 .125 1 0
Partition
1 Stop Here 101 3
m4 .0625 1 1 0 0
Partition
Stop 1100 4
m5 .0625 1 1 0
Partition
1 Stop 1101 4
m6 .0625 1 1 1 0
Partition
Stop 1110 4
m7 .03125 1 1 1 1 Partition 11110 5
m8 .03125 1 1 1 1 1 11111 5

13. Average codeword length (L)
Average codeword length L is given by,
L =
Where Pk = probability of kth message
mk = kth message
In the example discussed so far.
L = (1/2 X 1) + [(1/8 X 3)X 2] + [(1/16 X 4) X
3] + [(1/32 X 5) X2]
L = 2.3125 bits/message
13

14. Average information per message (H)
Average information per message (H) is given by
H =
Code efficiency (ŋ) :
Code efficiency (ŋ) is defined as the ratio of the average
information per message (H) and the average code word
length(L).
Code efficiency (ŋ) =
14

15. • There are no units for the code efficiency.
The code efficiency can be expressed in
percentage as,
• ŋ = x100 %
• The code efficiency should be as high as
possible.
15

16. • Soln.
• Follow the procedure given below to solve this
example :
• Step 1 : Calculate the average information per
message H
• Step 2 : Then calculate the average code word
length L
• Step 3 : Calculate information per binit.
• Step 4 : Obtain the code efficiency.
16
With reference to code created above(please take reference of
table) prove that each binit in the code words generated for
different message, carries the maximum possible information of
1 bit. Also calculate the code efficiency.

17. • Step 1 : The average information per message (H)
looking at table 2.5.2 the average information per
message is given as:
• H =
• = ½ log2 (2) + 2/8 log2 (8) + 3/16 log2 (16) + 2/32
log2 (32)
• = ½ + ¾ + ¾ + 5/16
• H = 2.3125 bits/message
17

18. • Step 2 : The average code word length L
Now find the average number of binits per message. As each
message is coded into different number of binits. Let us use their
probabilities to calculate average number of binits per message.
• L = average binits/message
= 1(1/2) + 3(1/8) + 4(1/16) + 4 (1/16) + 4(1/16) + 5(1/32) + 5(1/32)
L = 2.3125
• It is clear from the equations (2) and (3) that the average
information conveyed by each binit is 1 bit i.e. the maximum
possible information.
18

19. • If we do not follow this coding procedure then
to encode 8 different message we would
require 1 binits/message. But with coding we
need only 2.3125 binits/message as shown in
equation(3)
• Step 4 : Code effi ie ŋ :
ŋ = %
• Substituting the values, we get,
ŋ = %
19

20. The Shannon-Fano code is constructed as follows
20
Example . A discrete memory less source has five symbols x1, x2,
x3, x4, and x5, with probabilities p(x1) = 0.4, p(x2) = 0.19, p(x3) =
0.16, p(x4) = 0.15, and p(x5) = 0.1.
construct the shannon-Fano code and calculate the code
efficiency.
Message Probability Step 1 Step 2 Step 3 Code Code
length
x1 0.4 0 0 Partition 00 2
X2 0.19 0 Partition 1 01 2
X3 0.16 1 0 Partition 10 2
X4 0.15 1 1 0 Partition 110 3
x5 0.1 1 1 1 111 3

21. The average information per message (H)
H =
= 0.4 log2 (1/0.4) + 0.19 log2 (1/0.19)+ 0.16 log2
(1/0.16) + 0.15 log2 (1/0.15) + 0.1 log2 (1/0.1)
H = 2.15 bits/message
Average code word length(L)
L =
= (0.4x2)+(0.19x2)+(0.16x2)+(0.15x3)+(0.1x3)
L = 0.8+0.38+0.32+0.45+0.3
= 2.25 bits/message
21

22. Efficiency of the code ŋ :
• ŋ = %
= X100%
= 95.6%

23. • Follow the step given below to obtain the Shannon-Fano code.
• Step 1 : list the source symbols in the order of decreasing
probability.
• Step 2 : Partition the set into two sets that are as close to being
equiprobable as possible and assign 0 to the upper set and 1 to the
lower set.
• Step 3 : Continue this process, each time partitioning the sets with
as nearly equal probabilities as possible until further partitioning is
not possible.
Ex. A discrete memory less source has five symbols x1, x2, x3, x4, and x5, with
probabilities p(x1) = 0.4, p(x2) = 0.19, p(x3) = 0.16, p(x4) = 0.14, and p(x5) =
0.11.
construct the shannon-Fano code for this source. Calculate the average code
word length and coding efficiency of the source.

24. • The Shannon-Fano codes are given
Symbols Probability Step 1 Step2 Step 3 Code
word
x1 0.4 0 0
Partition
Stop
here
00
x1 0.19 0 Partition 1 Stop
here
01
x1 0.16 1 0
Partition
Stop
here
10
x1 0.14 1 1 0 Partition Stop
here
110
x1 0.11 1 1 1 Stop
here
111

25. • Average code word length (L)
• Average code word length (L) is given by:
• L =
• = (0.4x2) + (0.19x2) + (0.16x2) + (0.14x3) +
(0.11x3)
• 2.25 bits/message

26. • Entropy of the source (H):
• H =
• = 0.4 log2 (1/0.4) + 0.19 log2 (1/0.19) + 0.16
log2 (1/0.16) + 0.14 log2 (1/0.14) + 0.11 log2
(1/0.11)
• H= 2.15

27. Example : A message comprising of different characters which are
transmitted over a data link. The relative frequency of occurrence of
each character is –
A = 0.1, B = 0.25, C = 0.05, D = 0.32, E = 0.01, F = 0.07, G = 0.2
Drive the entropy of the message and derive the suitable set of code
words using Shannon-Fano coding.
• Solution
Given
X A B C D E F G
P 0.1 0.25 0.05 0.32 0.01 0.07 0.2
RGPV Question

28. • H =
= - [0.1 log 0.1 + 0.25 log 0.25 + 0.05 log 0.05 +
0.32 log 0.32 + 0.01 log 0.01 + 0.07 log 0.07 +
0.2 log 0.2]
= 0.714 bits/message


7
1
kPlog
k
kP

29. • Code words by using Shannon-Fano coding
X D B G A F C E
P 0.32 0.25 0.2 0.1 0.07 0.05 0.01
DBGAFCE
DB
D B
GAFCE
GE
E G
AFC
A FC
F C
0 1 0 1
0
1 0
1
0
1
0 1

30. • Encoded message length (n)
• D = 00 2
• B = 01 2
• G = 100 3
• E = 101 3
• A = 110 3
• F = 1110 4
• C = 1111 5

31. Thank You
Dr Rajiv Srivastava
Director
Sagar Institute of Research & Technology (SIRT)
Sagar Group of Institutions, Bhopal
http://www.sirtbhopal.ac.in