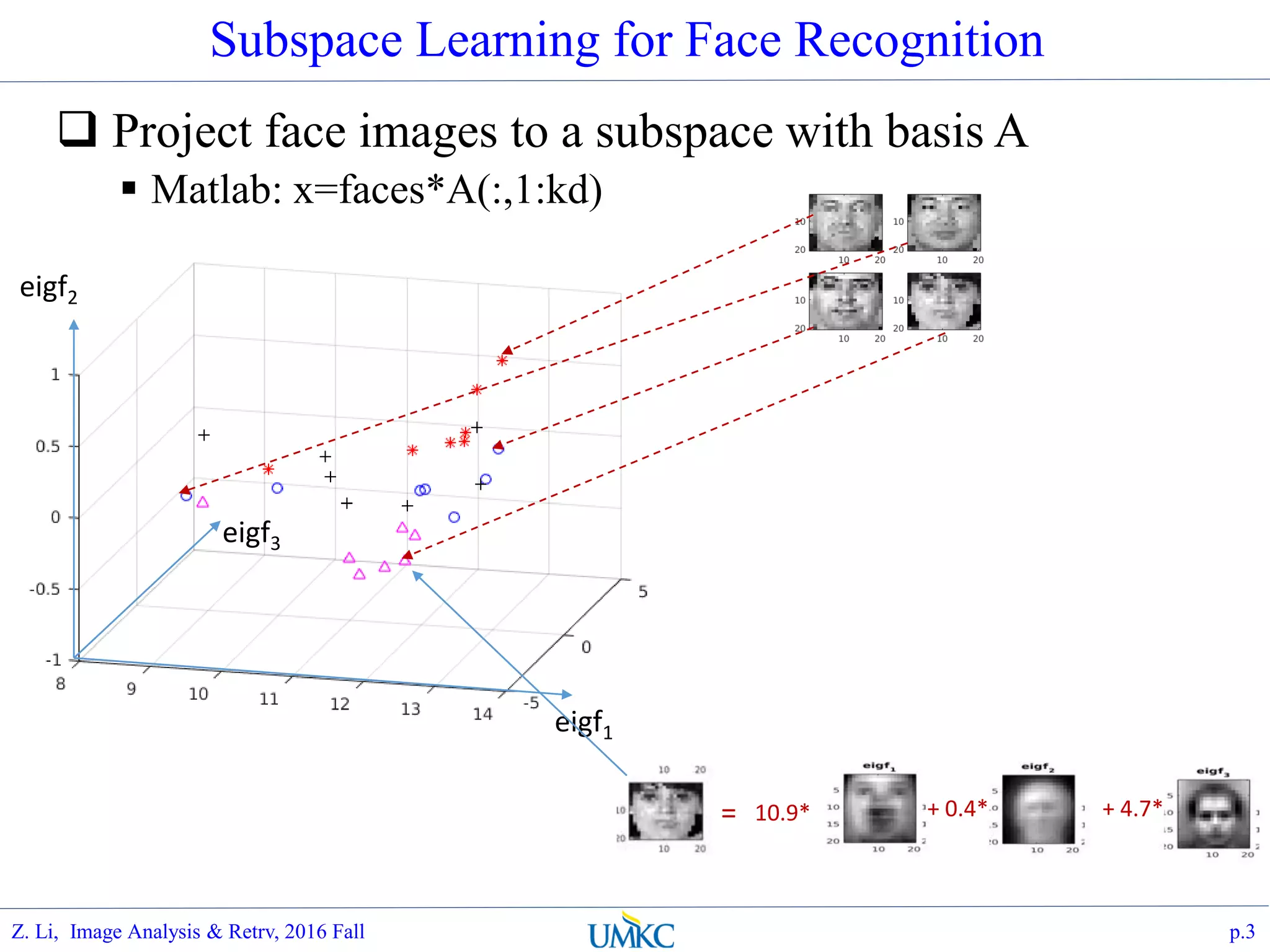
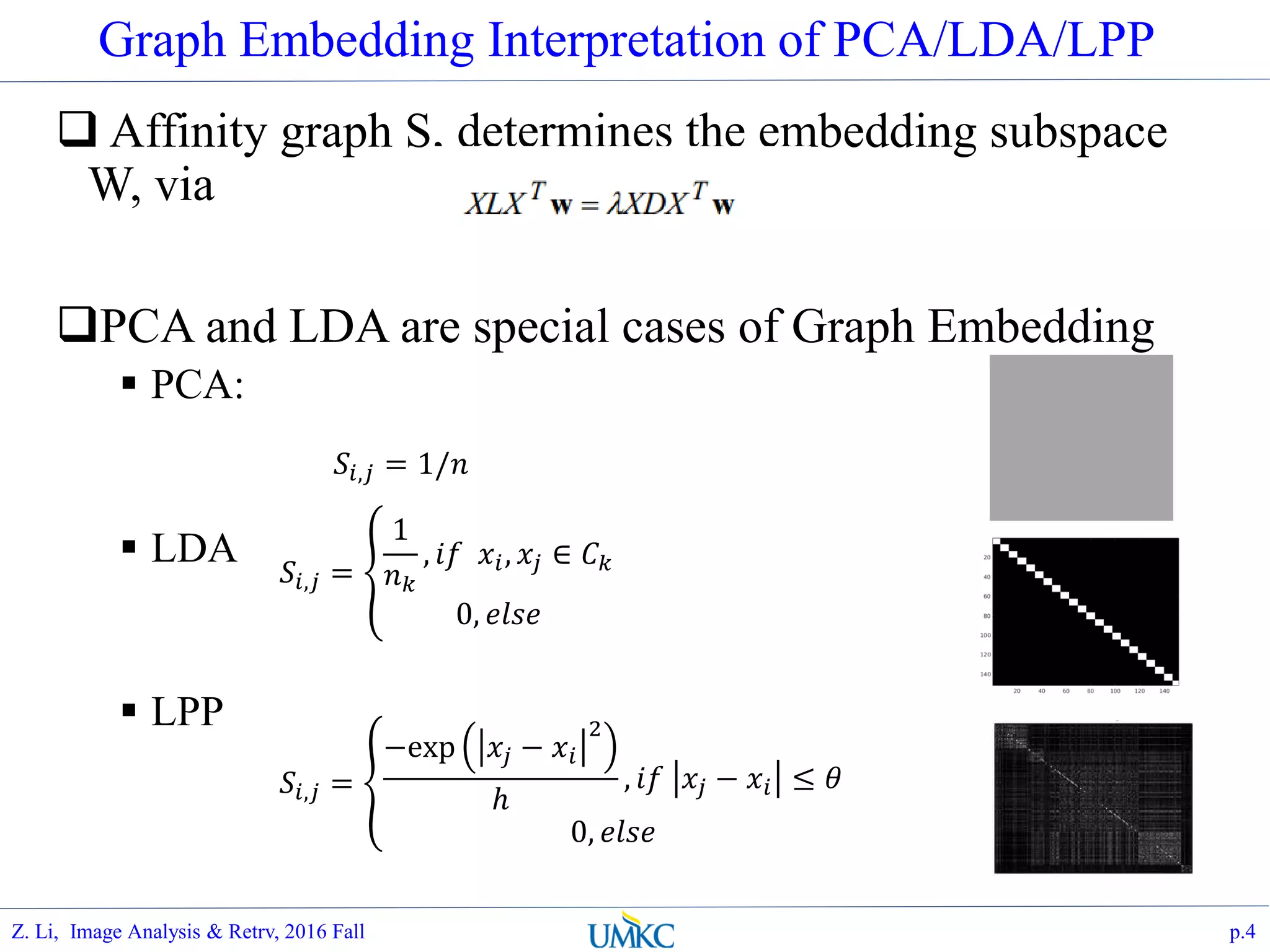
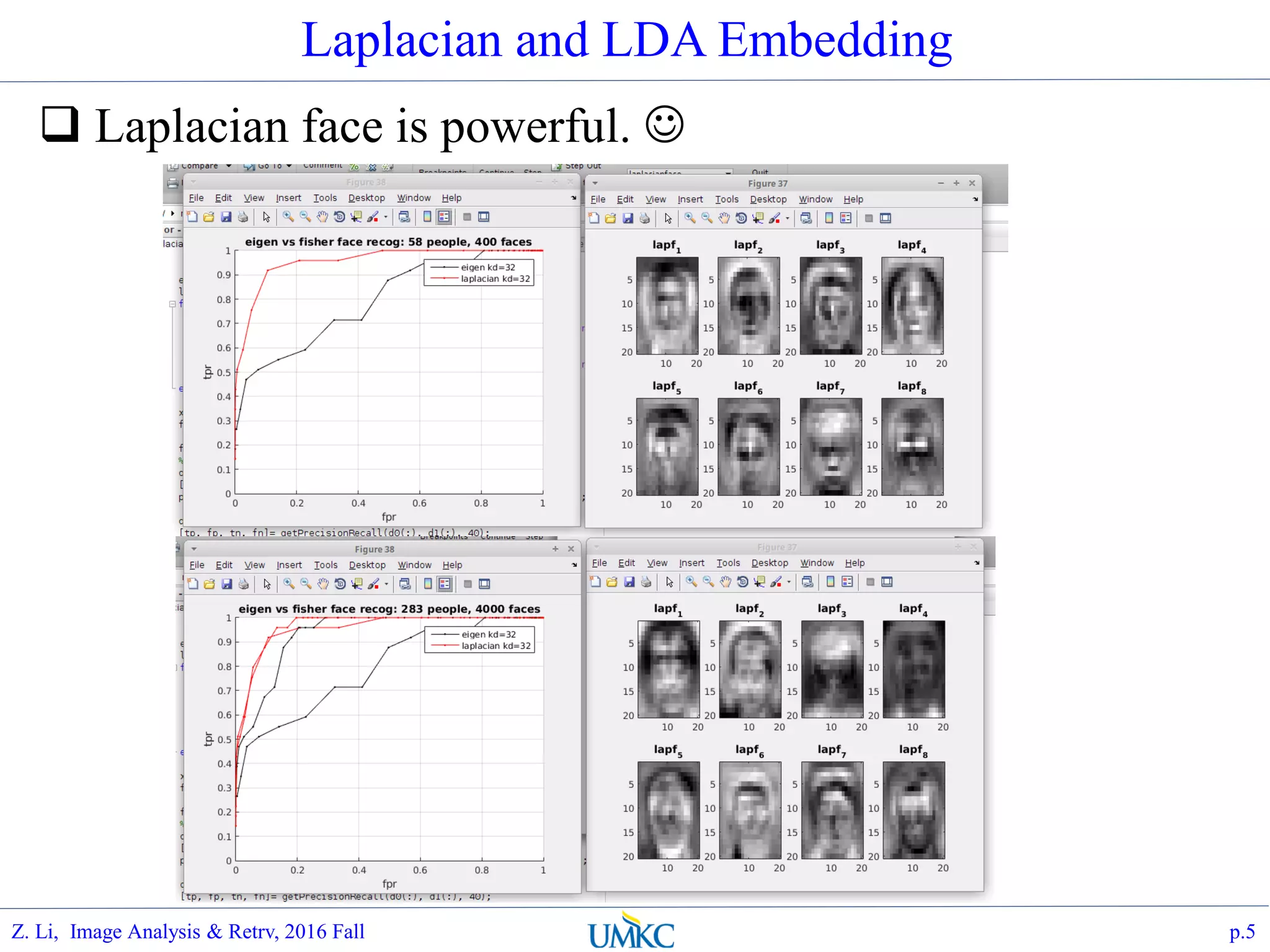
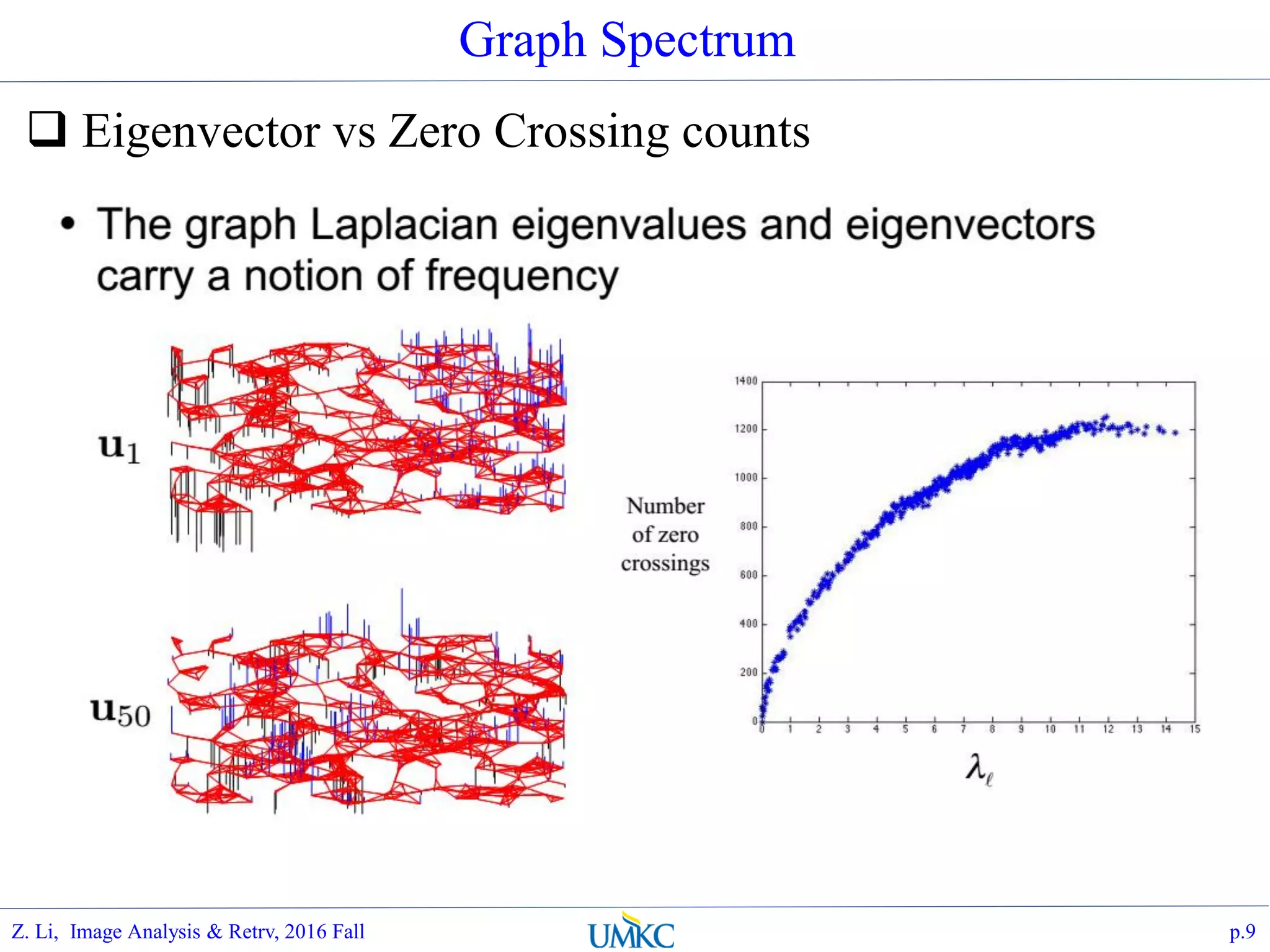
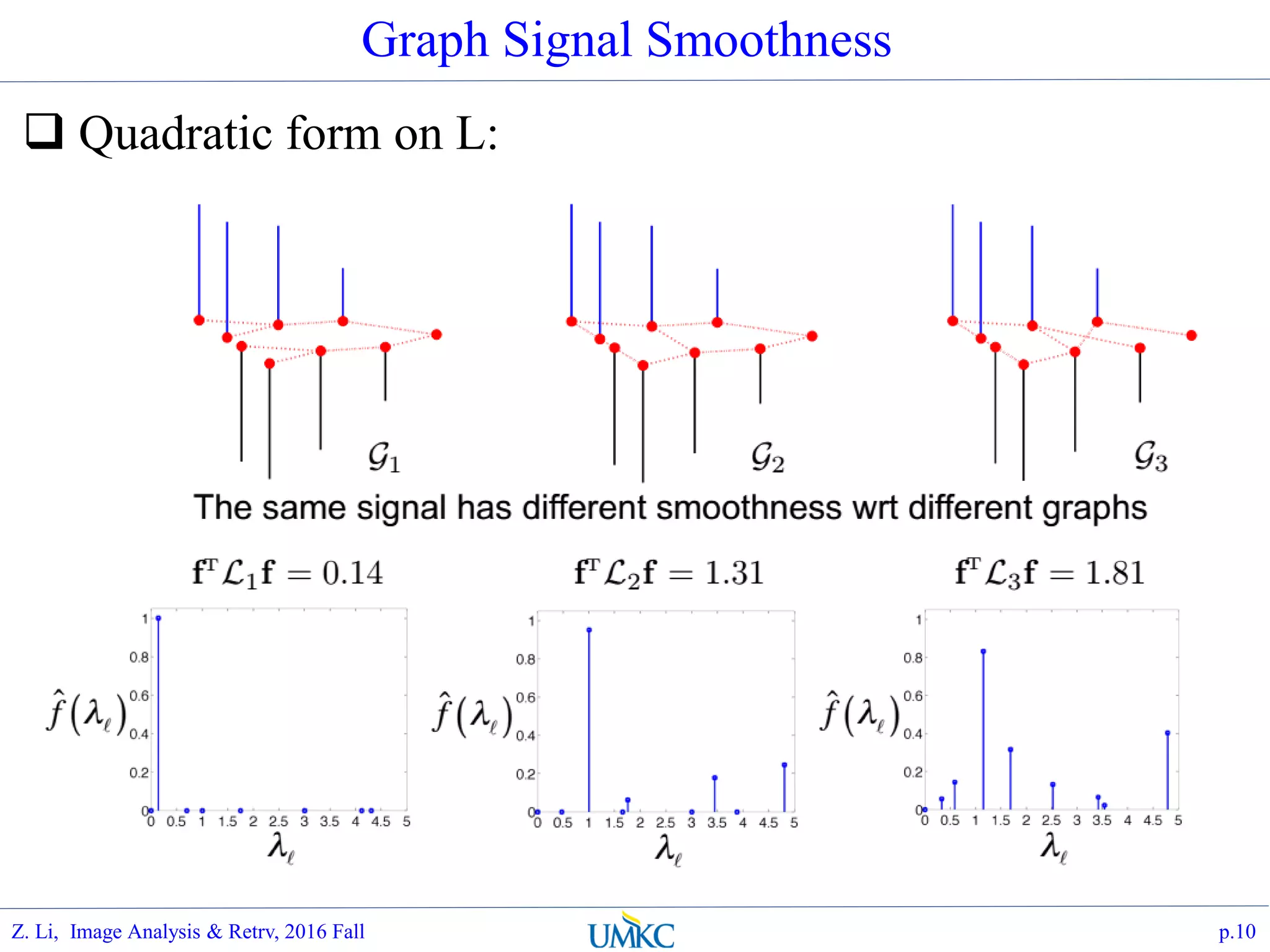
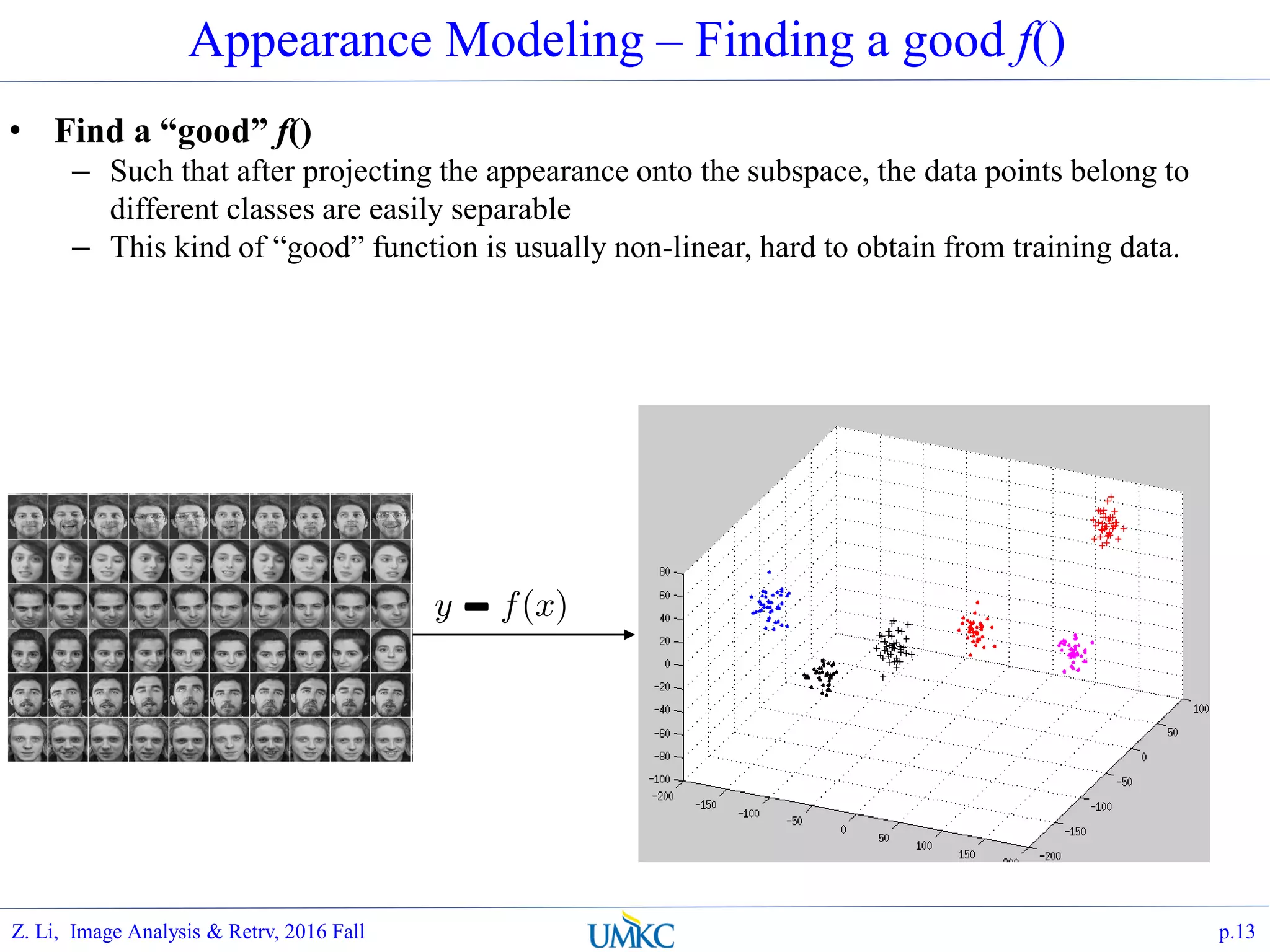
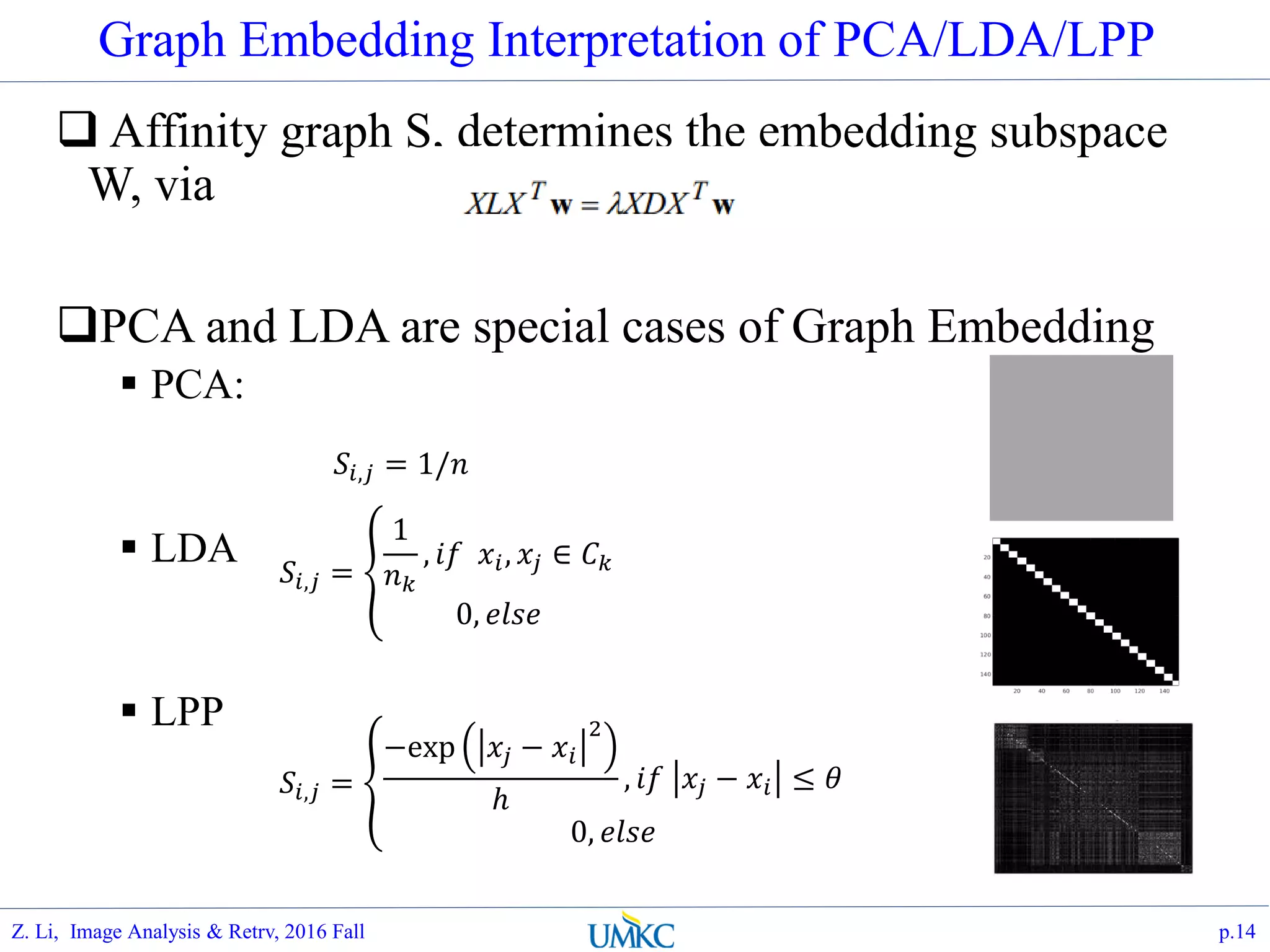
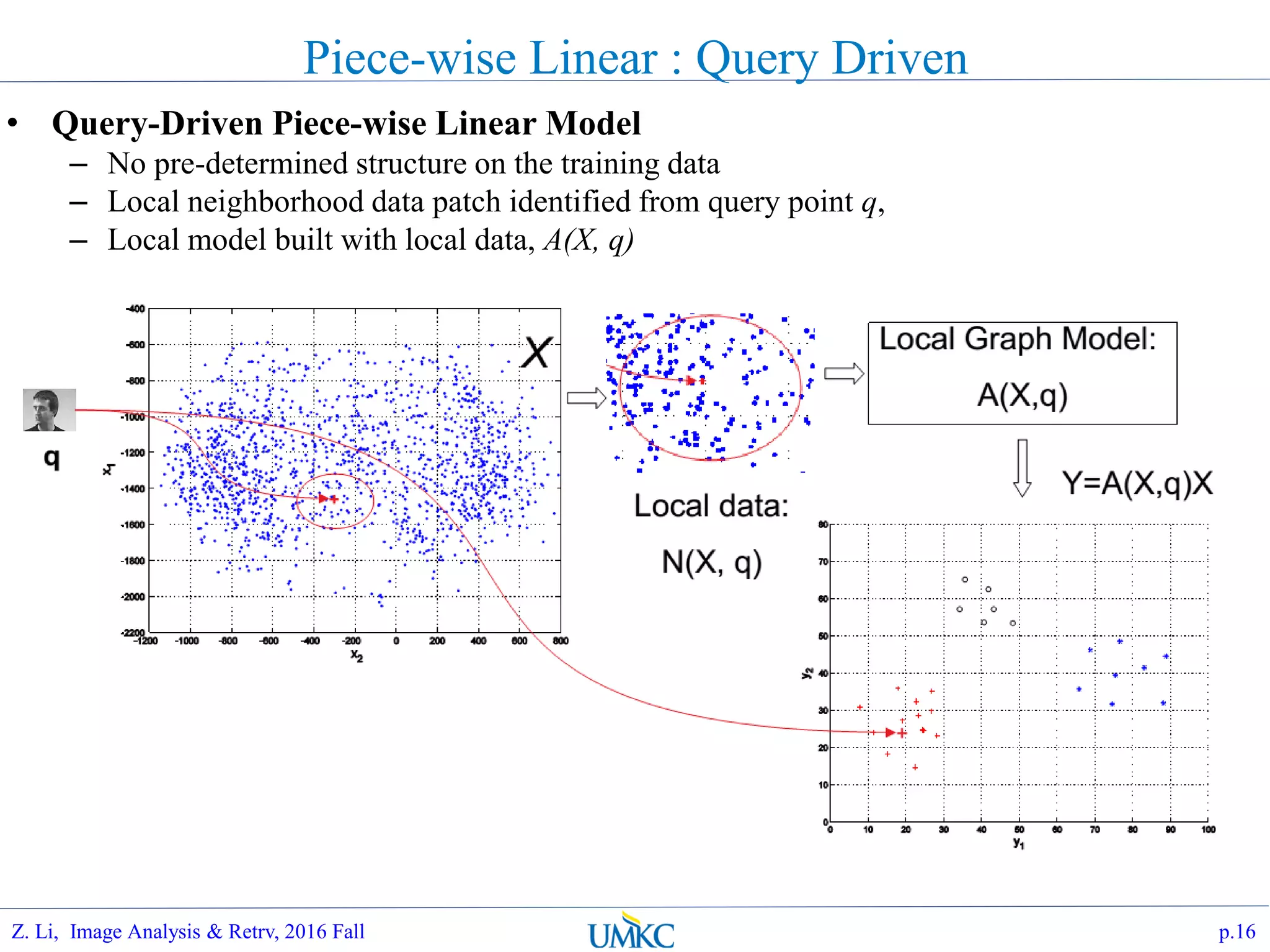
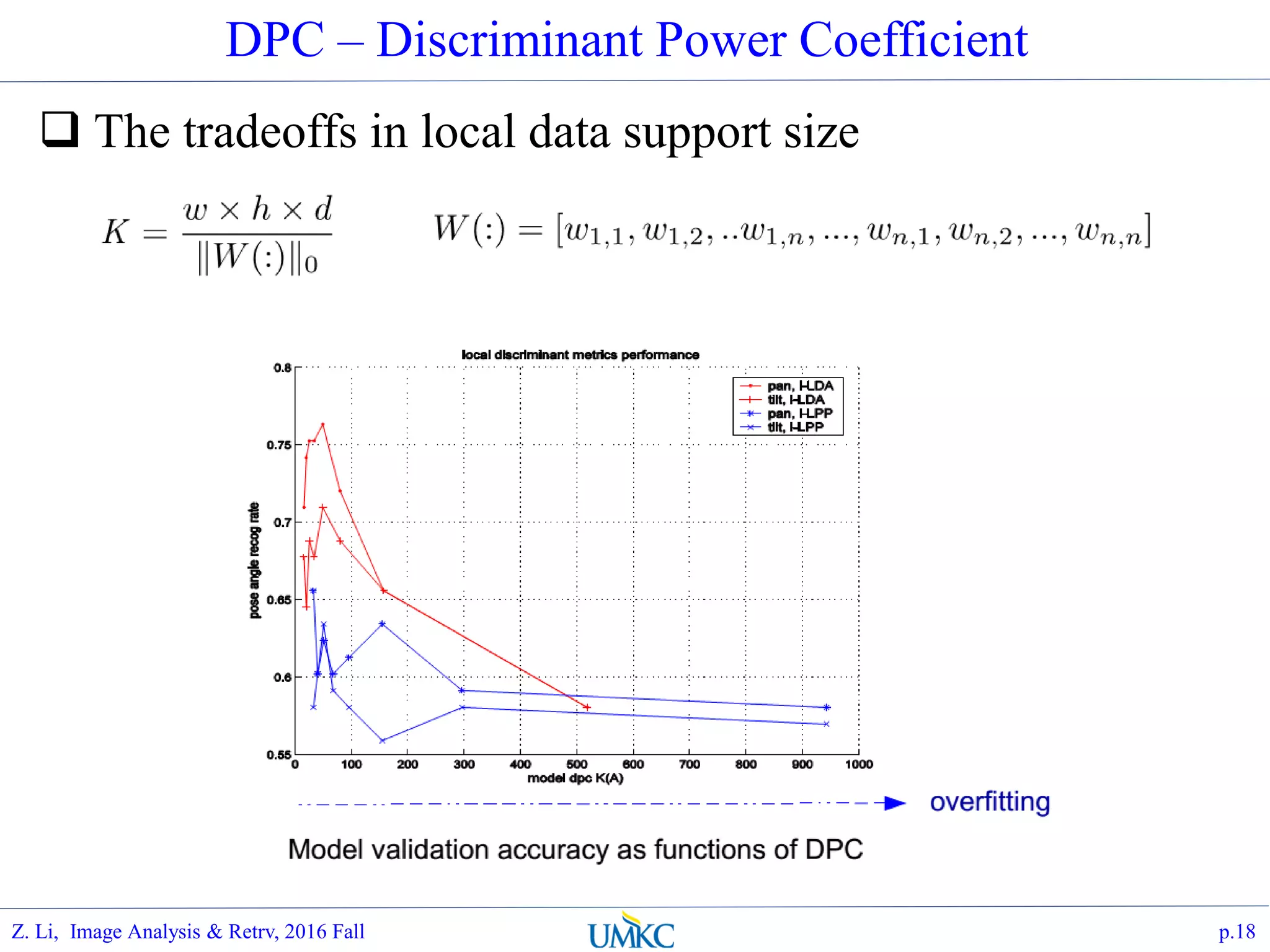
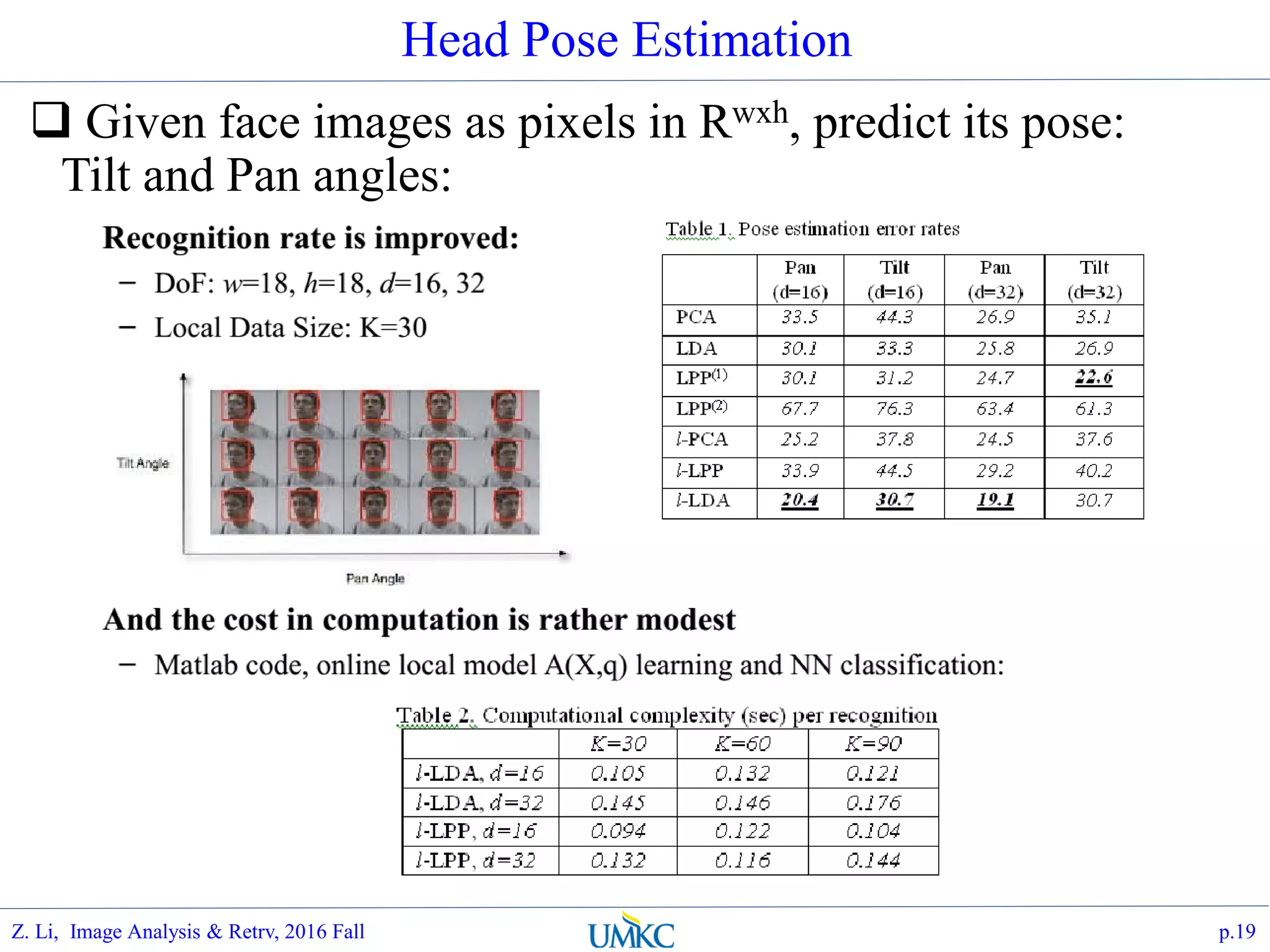
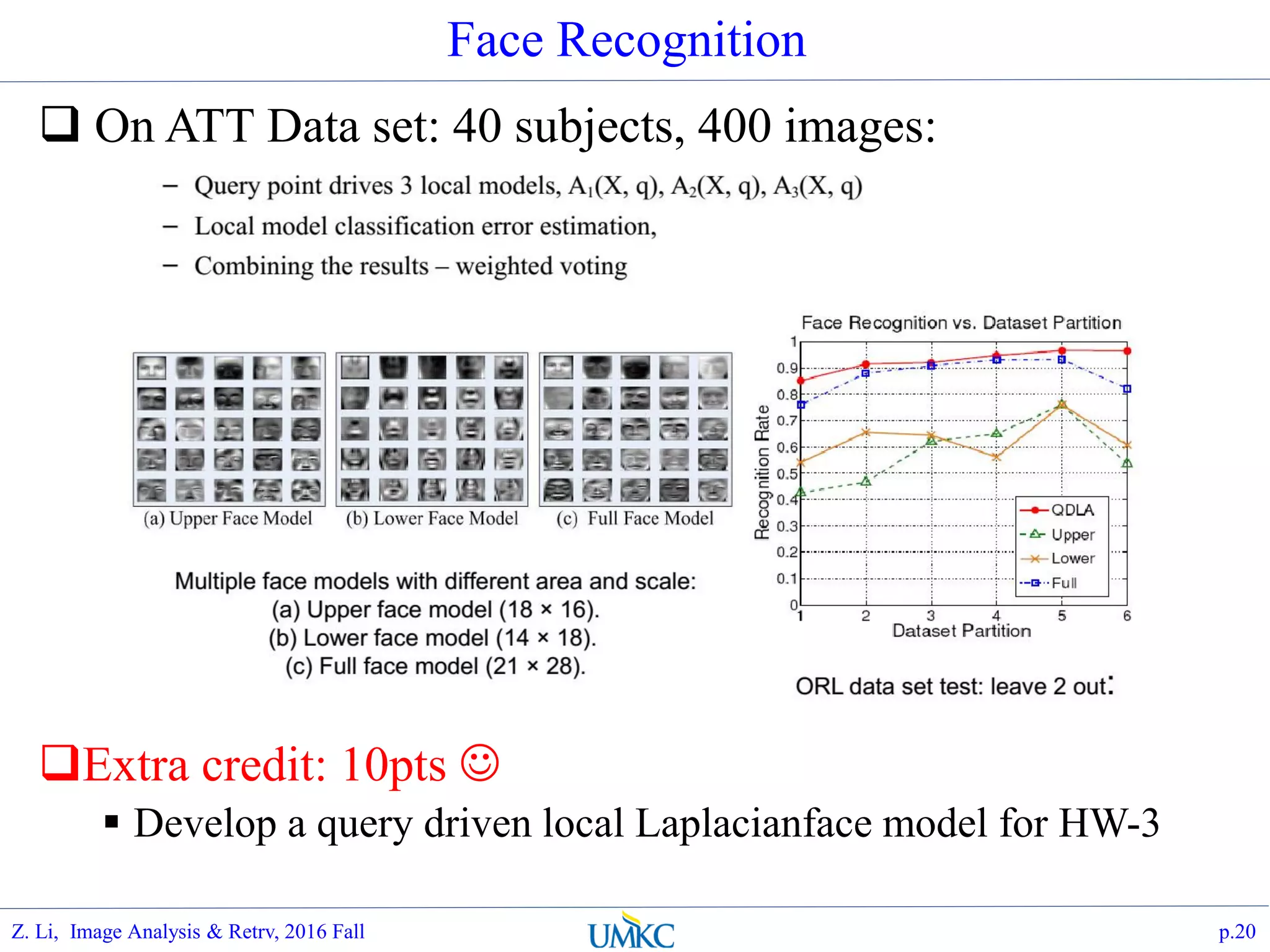
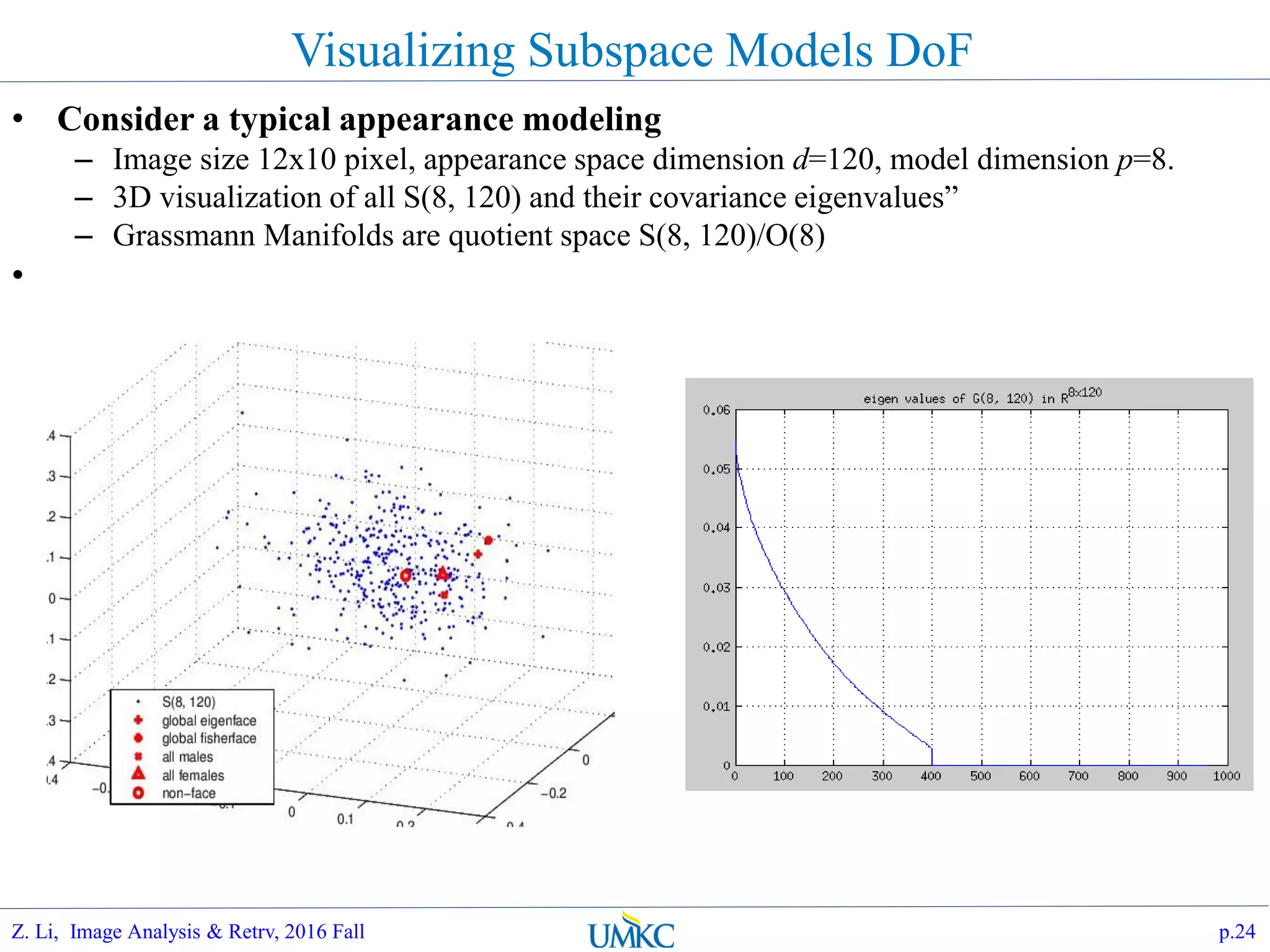
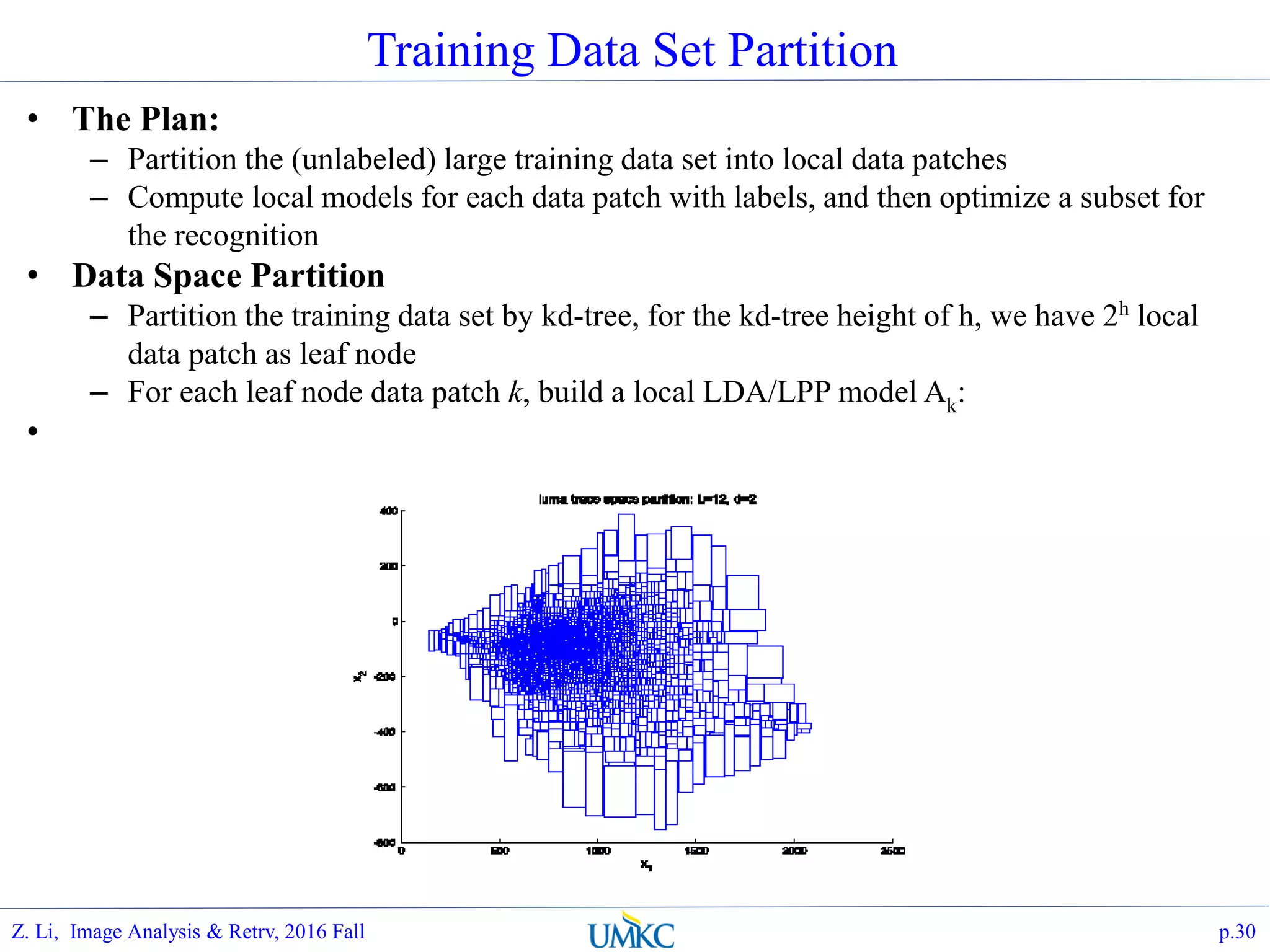
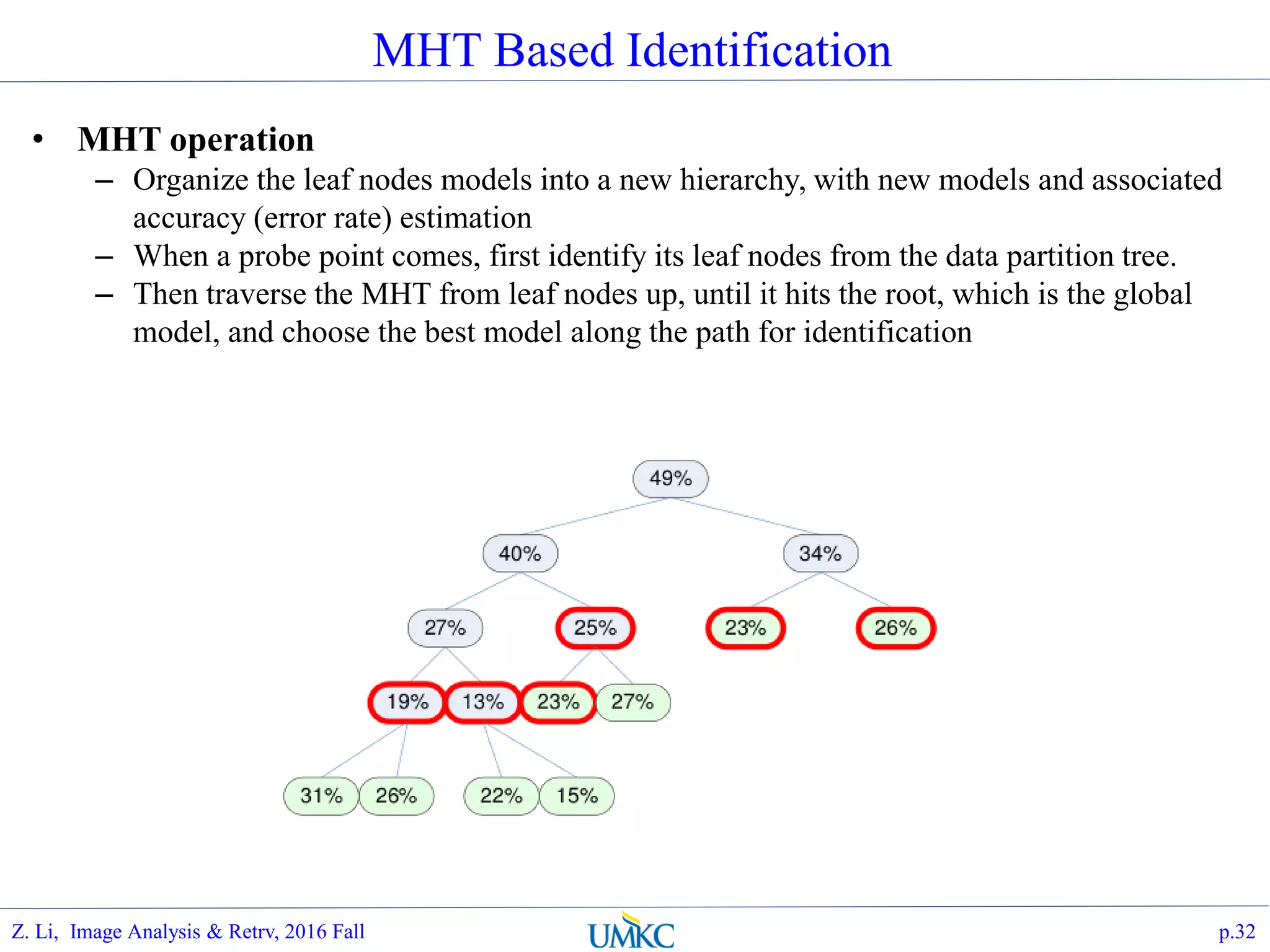
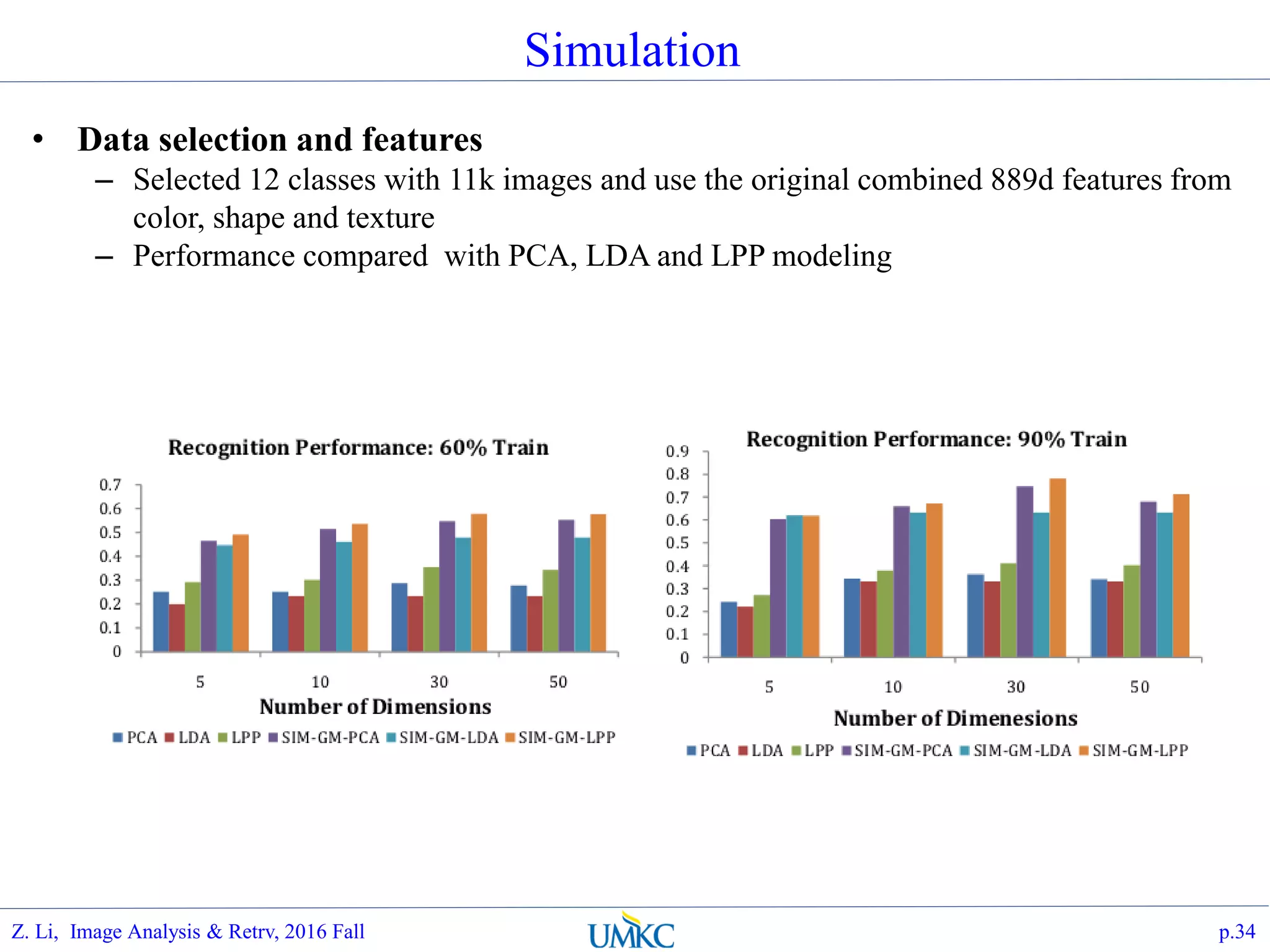
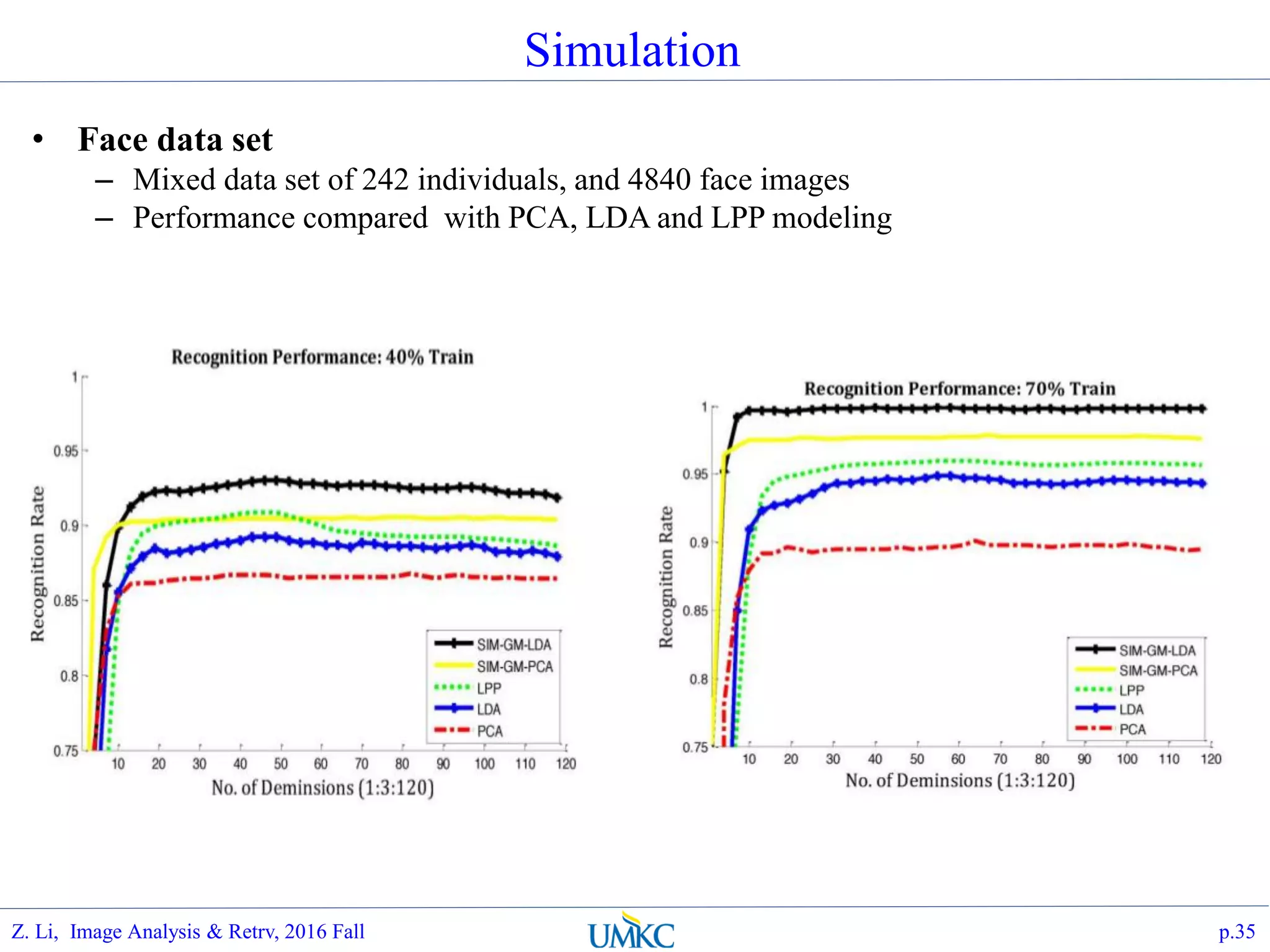
The document outlines a course on image analysis and retrieval, focusing on subspace optimization techniques and their applications in face recognition, image search, and fingerprint identification. It discusses various mathematical approaches, including graph Fourier transform and local models, to improve classification and recognition tasks while addressing challenges in handling large datasets. The document also highlights future work related to Grassmann hashing and indexing methods to enhance performance in visual recognition problems.