Arithmetic coding

Gabriele Monfardini - Corso di Basi di Dati Multimediali a.a. 2005-20062
How we can do better than
Huffman? - I
 As we have seen, the main drawback of
Huffman scheme is that it has problems when
there is a symbol with very high probability
 Remember static Huffman redundancy bound
where is the probability of the most likely
simbol
1redundancy 0.086p≤ +
1p

Huffman? - II
 The only way to overcome this limitation is to
use, as symbols, “blocks” of several
characters.
In this way the per-symbol inefficiency is
spread over the whole block
 However, the use of blocks is difficult to
implement as there must be a block for every
possible combination of symbols, so block
number increases exponentially with their
length

Huffman? - III
 Huffman Coding is optimal in its
framework
 static model
 one symbol, one word
adaptive Huffman
blocking
arithmetic
coding

The key idea
 Arithmetic coding completely bypasses the
idea of replacing an input symbol with a
specific code.
 Instead, it takes a stream of input symbols
and replaces it with a single floating point
number in
 The longer and more complex the message, the
more bits are needed to represents the output
number
[0,1)

The key idea - II
 The output of an arithmetic coding is, as usual,
a stream of bits
 However we can think that there is a prefix 0,
and the stream represents a fractional binary
number between 0 and 1
 In order to explain the algorithm, numbers will
be shown as decimal, but obviously they are
always binary
01101010 0110 00. 101→

An example - I
 String bccb from the alphabet {a,b,c}
 Zero-frequency problem solved initializing at 1
all character counters
 When the first b is to be coded all symbols
have a 33% probability (why?)
 The arithmetic coder maintains two numbers,
low and high, which represent a subinterval
[low,high) of the range [0,1)
 Initially low=0 and high=1

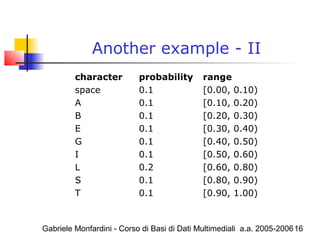
An example - II
 The range between low and high is divided
between the symbols of the alphabet,
according to their probabilities
low
high
0
1
0.333
3
0.666
7
a
b
c(P[c]=1/3)
(P[b]=1/3)
(P[a]=1/3)

9
An example - III
low
high
0
1
0.333
3
0.666
7
a
b
c
b
low = 0.3333
high = 0.6667
 P[a]=1/4
 P[b]=2/4
 P[c]=1/4
new probabilities

An example - IV
new probabilities
 P[a]=1/5
 P[b]=2/5
 P[c]=2/5
low
high
0.333
3
0.666
7
0.416
7
0.583
4
a
b
c
c
low = 0.5834
high = 0.6667
(P[c]=1/4)
(P[b]=2/4)
(P[a]=1/4)

An example - V
new probabilities
 P[a]=1/6
 P[b]=2/6
 P[c]=3/6
low
high
0.583
4
0.666
7
0.600
1
0.633
4
a
b
c
c
low = 0.6334
high = 0.6667
(P[c]=2/5)
(P[b]=2/5)
(P[a]=1/5)

An example - VI
 Final interval
[0.6390,0.6501)
 we can send 0.64
low
high
0.633
4
0.666
7
0.639
0
0.650
1
a
b
c
low = 0.6390
high = 0.6501
b
(P[c]=3/6)
(P[b]=2/6)
(P[a]=1/6)

An example - summary
 Starting from the range between 0 and 1 we
restrict ourself each time to the subinterval
that codify the given symbol
 At the end the whole sequence can be codified
by any of the numbers in the final range (but
mind the brackets...)

14
An example - summary
0
1
0.333
3
0.666
7
a
b
c
0.6667
0.3333
1/3
1/3
1/3
0.4167
0.5834
1/4
2/4
1/4
a
b
c
0. 5834
0. 6667
2/5
2/5
1/5
0.6001
0.6334
a
b
c
0. 6667
0.6334 a
b
c
0.6390
0.6501
3/6
2/6
1/6
[0.6390, 0.6501) 0.64

Another example - I
 Consider encoding the name BILL GATES
Again, we need the frequency of all the
characters in the text.
chr freq.
space 0.1
A 0.1
B 0.1
E 0.1
G 0.1
I 0.1
L 0.2
S 0.1
T 0.1

Another example - II
character probability range
space 0.1 [0.00, 0.10)
A 0.1 [0.10, 0.20)
B 0.1 [0.20, 0.30)
E 0.1 [0.30, 0.40)
G 0.1 [0.40, 0.50)
I 0.1 [0.50, 0.60)
L 0.2 [0.60, 0.80)
S 0.1 [0.80, 0.90)
T 0.1 [0.90, 1.00)

Another example - III
chr low high
0.0 1.0
B 0.2 0.3
I 0.25 0.26
L 0.256 0.258
L 0.2572 0.2576
Space 0.25720 0.25724
G 0.257216 0.257220
A 0.2572164 0.2572168
T 0.25721676 0.2572168
E 0.257216772 0.257216776
S 0.2572167752 0.2572167756
The final low value, 0.2572167752 will uniquely encode
the name BILL GATES

Decoding - I
 Suppose we have to decode 0.64
 The decoder needs symbol probabilities, as it
simulates what the encoder must have been
doing
 It starts with low=0 and high=1 and divides
the interval exactly in the same manner as the
encoder (a in [0, 1/3), b in [1/3, 2/3), c in
[2/3, 1)

Decoding - II
 The trasmitted number falls in the interval
corresponding to b, so b must have been the
first symbol encoded
 Then the decoder evaluates the new values for
low (0.3333) and for high (0.6667), updates
symbol probabilities and divides the range
from low to high according to these new
probabilities
 Decoding proceeds until the full string has
been reconstructed

Decoding - III
 0.64 in [0.3333, 0.6667) b
 0.64 in [0.5834, 0.6667) c...
and so on...

Why does it works?
 More bits are necessary to express a number
in a smaller interval
 High-probability events do not decrease very
much interval range, while low probability
events result a much smaller next interval
 The number of digits needed is proportional to
the negative logarithm of the size of the
interval

Why does it works?
 The size of the final interval is the product of
the probabilities of the symbols coded, so the
logarithm of this product is the sum of the
logarithm of each term
 So a symbol s with probability Pr[s]
contributes
bits to the output, that is equal to symbol
probability content (uncertainty)!!
log Pr[ ]s−

Why does it works?
 For this reason arithmetic coding is nearly
optimum as number of output bits, and it is
capable to code very high probability events in
just a fraction of bit
 In practice, the algorithm is not exactly
optimal because of the use of limited precision
arithmetic, and because trasmission requires
to send a whole number of bits

A trick - I
 As the algorithm was described until now, the
whole output is available only when encoding
are finished
 In practice, it is possible to output bits during
the encoding, which avoids the need for higher
and higher arithmetic precision in the encoding
 The trick is to observe that when low and high
are close they could share a common prefix

A trick - II
 This prefix will remain forever in the two
values, so we can transmit it and remove from
low and high
 For example, during the encoding of “bccb”, it
has happened that after the encoding of the
third character the range is low=0.6334,
high=0.6667
 We can remove the common prefix, sending 6
to the output and transforming low and high
into 0.334 and 0,667

The encoding step
 To code symbol s, where symbols are
numbered from 1 to n and symbol i has
probability Pr[i]
 low_bound =
 high_bound =
 range = high - low
 low = low + range * low_bound
 high = low + range * high_bound
1
1
Pr[ ]
s
i
i
−
=∑
1
Pr[ ]
s
i
i=∑

The decoding step
 The symbols are numbered from 1 to n and
value is the arithmetic code to be processed
 Find s such that
 Return symbol s
 Perform the same range-narrowing step of the encoding step
1
1 1
( )
Pr[ ] Pr[ ]
( )
s s
i i
value low
i i
high low
−
= =
−
≤ ≤
−
∑ ∑

Implementing arithmetic coding
 As mentioned early, arithmetic coding uses
binary fractional number with unlimited
arithmetic precision
 Working with finite precision (16 or 32 bits)
causes compression be a little worser than
entropy bound
 It is possible also to build coders based on
integer arithmetic, with another little
degradation of compression

29
Arithmetic coding vs. Huffman coding
 In tipical English text, the space character is
the most common, with a probability of about
18%, so Huffman redundancy is quite small.
Moreover this is an upper bound
 On the contrary, in black and white images,
arithmetic coding is much better than Huffman
coding, unless a blocking technique is used
A A. coding requires less memory, as symbol
representation is calculated on the fly
A A. coding is more suitable for high
performance models, where there are
confident predictions

Arithmetic coding vs. Huffman coding
H H. decoding is generally faster than a.
decoding
H In a. coding it is not easy to start decoding in
the middle of the stream, while in H. coding
we can use “starting points”
 In large collections of text and images,
Huffman coding is likely to be used for the
text, and arithmeting coding for the images

Arithmetic coding

More Related Content

What's hot

Viewers also liked

Similar to Arithmetic coding

Recently uploaded

Arithmetic coding