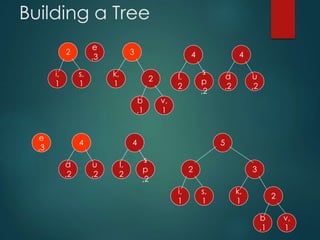
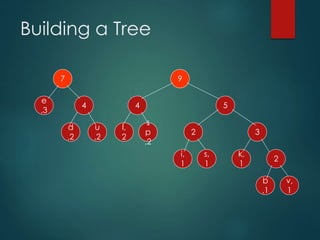
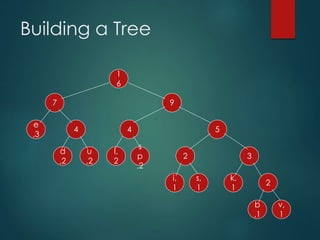
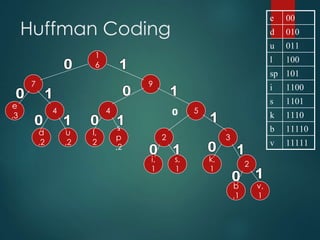
This presentation summarizes Huffman coding. It begins with an outline covering the definition, history, building the tree, implementation, algorithm and examples. It then discusses how Huffman coding encodes data by building a binary tree from character frequencies and assigning codes based on the tree's structure. An example shows how the string "Duke blue devils" is encoded. The time complexity of building the Huffman tree is O(NlogN). Real-life applications of Huffman coding include data compression in fax machines, text files and other forms of data transmission.

1. NAME : NAZMUL HYDER
ID : 011 -131-085
WELCOME TO MY
PRESENTATION
Topic: Huffman Coding

2. Outline
✓ Definition of The Problem
✓ History
✓ Building the tree
✓ Implementation
✓Algorithm
✓Example
✓ Run Time Analysis
✓ Applications

3. Encoding and
Compression of Data
▶ Fax Machines
▶ ASCII
▶ Variations on ASCII
▶ min number of bits needed
▶ cost of savings
▶ patterns
▶ modifications

4. Purpose of Huffman
Coding
▶ Proposed by Dr. David A. Huffman in 1952
▶ “A Method for the Construction of Minimum
Redundancy Codes”
▶ Applicable to many forms of data transmission
▶ Our example: text files

5. Human Coding
Create New Node m
1. frequencies[m] ←
frequency1 + frequency2 // new
node
2. frequencies[node1] ← m // left link
3. frequencies[node2] ← -m // right link
4. insert in PQueue
(m, frequency1 + frequency2)

6. Huffman Coding
▶ As an example, lets take the string:
“Duke blue devils”
▶ We first to a frequency count of the characters:
▶ S:1, i:1, v:1, b:1, k:1, sp:2, l:2, u:2, d:2, e:3.
▶ Next we use a Greedy algorithm to build up a Huffman Tree
▶ We start with nodes for each character
e
,3
d
,2
u
,2
l,
2
s
p
,2
k,
1
b
,1
v,
1
i,
1
S,
1

7. Building a Tree
e
,3
d
,2
u
,2
l,
2
s
p
,2
k,
1
b
,1
v,
1
i,
1
s,
1
e
,3
d
,2
u
,2
l,
2
s
p
,2
k,
1
b
,1
v,
1
i,
1
s,
1
2
e
,3
d
,2
u
,2
l,
2
s
p
,2
k,
1
b
,1
v,
1
i,
1
s,
1
22

8. Building a Tree
e
,3
d
,2
u
,2
l,
2
s
p
,2
k,
1
i,
1
s,
1
2
b
,1
v,
1
2
3
e
,3
d
,2
u
,2
l,
2
s
p
,2
k,
1
i,
1
s,
1
2
b
,1
v,
1
2
3 4

9. Building a Tree
e
,3
d
,2
u
,2
l,
2
s
p
,2
k,
1
i,
1
s,
1
2
b
,1
v,
1
2
3 4 4
e
,3
d
,2
u
,2
l,
2
s
p
,2
k,
1
i,
1
s,
1
2
b
,1
v,
1
2
3
44 5

10. Building a Tree
e
,3
d
,2
u
,2
l,
2
s
p
,2
k,
1
i,
1
s,
1
2
b
,1
v,
1
2
3
4
4
5 7

11. Building a Tree
e
,3
d
,2
u
,2
l,
2
s
p
,2
k,
1
i,
1
s,
1
2
b
,1
v,
1
2
3
44 5
7 9

12. Building a Tree
e
,3
d
,2
u
,2
l,
2
s
p
,2
k,
1
i,
1
s,
1
2
b
,1
v,
1
2
3
44 5
7 9
1
6

13. Huffman Coding
▶ Once receiver has tree it scans incoming bit stream
▶ 0 Go left.
▶ 1 Go right.
▶ Note that no code is the prefix of another code

14. Huffman Coding
e
,3
d
,2
u
,2
l,
2
s
p
,2
k,
1
i,
1
s,
1
2
b
,1
v,
1
2
3
44 5
7 9
1
6
e 00
d 010
u 011
l 100
sp 101
i 1100
s 1101
k 1110
b 11110
v 11111
0

15. Encoding the String results
▶ These codes are then used to encode the string
▶ Thus, “duke blue devils” turns into 56 bits:
010 011 1110 00 101 11110 100 011 00 101 010 00 11111
1100 100 1101
▶ ASCII will take 128 bit:
01001111 10001011 11101000 11001010 10001111
11100100 1101xxxx
h If modified code used 4 bits per character are
needed. Total bits
4 * 16 = 64. Savings not as great
▶ Thus it takes 7 bytes of space compared to 16
characters * 1 byte/char = 16 bytes uncompressed
▶ Total save=128-56=72.

16. Running Time
16
Time efficiency of building the Huffman
tree
The insert and delete operations each
take log(N) time, and they are repeated
at most 2N times
Therefore the run time is O(2NlogN) =
O(NlogN)

17. Real-Life Applications

18. That’s it.
Thank you