ECC module 1 & 2 SLIDESHARE_watermark.pdf

Department of Studies in Electronics &Communication Engg.,
University B.D.T. College of Engineering
Visveswaraya Technological University, Davanagere-4
Karnataka, India
Dr.T.D. Shashikala
12-2-2024

Course Code: 22LDN325 Credits: 3 Exam Hours: 3
CIE Marks: 50M SEE Marks: 50M Total Marks: 100
Teaching Hours/Week (L:P:SDA): (3:0:0) Total Hours of Pedagogy: 40 hours Theory
ERROR CONTROL CODING
Course Learning objectives: This course will enable students to:
• Understand the concept of the Entropy, information rate and capacity for the Discrete memoryless
channel.
• Apply modern algebra and probability theory for the coding.
• Compare Block codes such as Linear Block Codes, Cyclic codes, etc. and Convolutional codes.
• Detect and correct errors for different data communication and storage systems.
• Analyze and implement different Block code encoders and decoders, and also convolutional encoders and
decoders including soft and hard Viterbi algorithm.

Textbooks:
1. 'Digital Communication systems', Simon Haykin, Wiley India Private. Ltd, ISBN 978-
81-265-4231-4, First edition, 2014
2. 'Error control coding', Shu Lin and Daniel J. Costello. Jr, Pearson, Prentice Hall, 2nd
edition, 2004

Course outcome (Course Skill Set)
CO1: Understand the concept of the Entropy, information rate and capacity for the Discrete
memoryless channel.
CO2: Apply modern algebra and probability theory for the coding.
CO3: Compare Block codes such as Linear Block Codes, Cyclic codes, etc. and Convolutional
codes.
CO4: Detect and correct errors for different data communication and storage systems.
CO5: Analyze and implement different Block code encoders and decoders, and also
convolutional encoders and decoders including soft and hard Viterbi algorithm.

Reference Books:
1. 'Theory and practice of error control codes', Blahut. R. E, Addison Wesley, 1984
2. 'Introduction to Error control coding', Salvatore Gravano, Oxford University Press,
2007
3. 'Digital Communications - Fundamentals and Applications', Bernard Sklar, Pearson
Education (Asia) Pvt. Ltd., 2nd Edition, 2001
• Web links and Video Lectures (e-Resources):
• Skill Development Activities Suggested
• NPTEL Course on Information Theory and Coding

Assessment Details (both CIE and SEE)
The weightage of Continuous Internal Evaluation (CIE) is 50% and for Semester End
Exam (SEE) is 50%.
The minimum passing mark for the CIE is 50% of the maximum marks. Minimum
passing marks in SEE is 40% of the maximum marks of SEE.
Astudent shall be deemed to have satisfied the academic requirements and earned the credits allotted to
each subject/ course if the student secures not less than 50% (50 marks out of 100) in the sum total of the
CIE (Continuous Internal Evaluation) and SEE (Semester End Examination) taken together.
Continuous Internal Evaluation:
➢ Three Unit Tests each of 20 Marks
➢ Two assignments each of 20 Marks or one Skill DevelopmentActivity of 40 marks
to attain the COs and POs
➢ The sum of three tests, two assignments/skill DevelopmentActivities, will be scaled down to 50
marks

CIE methods /question paper is designed to attain the different levels of Bloom’s
taxonomy as per the outcome defined for the course.
Semester End Examination:
➢ The SEE question paper will be set for 100 marks and the marks scored will be
proportionately reduced to 50.
➢ The question paper will have ten full questions carrying equal marks.
➢ Each full question is for 20 marks. There will be two full questions (with a maximum
of four sub-questions) from each module.
➢ Each full question will have a sub-question covering all the topics under a module.
➢ The students will have to answer five full questions, selecting one full question from
each module.

Introduction to algebra:
Groups, Fields, binary field
arithmetic, Construction of Galois
Fields GF (2m) and its properties,
(Only statements of theorems
without proof) Computation using
Galois field GF (2m) arithmetic,
Vector spaces and Matrices (Chap. 2
of Text 2).
Module-1
Information theory:
Introduction, Entropy, Source coding
theorem, discrete memoryless channel,
Mutual Information, Channel Capacity
Channel coding theorem (Chap. 5 of
Text 1).
Chalk and Talk and Power
Point Presentation

The purpose of a communication system is to transmit signals generated by a source of information
over a communication channel. Information theory provides mathematical tools to model and analyze
these systems, focusing on two key questions:
1. What is the minimum complexity below which a signal cannot be compressed?
2. What is the maximum transmission rate for error-free communication over a noisy channel?
These are addressed through:
Entropy: Measures the average uncertainty (or information content) of a source.
Channel Capacity: The maximum rate at which information can be reliably transmitted over a
channel.
If the source’s entropy is less than the channel’s capacity, error-free communication is
theoretically possible

Entropy
Entropy quantifies the average information content of a discrete source. For a random
variable S , which emits symbols sk with probabilities pk , entropy is given by:
H(S) = σ𝒌=𝟎
𝑲−𝟏
𝒑𝒌 𝒍𝒐𝒈𝟐(𝒑𝒌)
Properties:
1. Lower Bound: H(S) = 0 when one symbol has pk = 1 (no uncertainty).
2. Upper Bound: H(S) = log2(K) when all symbols are equally probable ( pk = 1/K ),
representing maximum uncertainty

Self-Information
The information gained when observing
an event S = sk is called self-
information:
I(sk) = -log2(pk)
I(sk) = 0 if pk = 1 (no information
gained).
Less probable events provide more
information (I(sk) > I(si) for pk < pi ).
For independent events, self-information
is additive.
Relative Entropy (Kullback-Leibler
Divergence)
The relative entropy between two probability
distributions p and q is:
D(p ∥ q) = σ𝑘=0
𝐾−1
𝑝𝑘 𝑙𝑜𝑔2(
𝑝𝑘
𝑞𝑘
)
D(p ∥ q) ≥ 0 , with equality only when p = q
For equiprobable distributions (qk = 1/K ),
this relationship shows that entropy H(S) is
maximized at log2(K) .

• Practical Implications of Entropy
• Helps in data compression.
• Provides limits for efficient
encoding.
• Determines channel capacity in
communication systems.

EXAMPLE 1 Entropy of Bernoulli Random Variable
Entropy provides a measure of uncertainty in a source,
essential for efficient signal compression and reliable
communication. It is bounded between 0 and log2(K) ,
depending on the probability distribution of the source
symbols.

Source Coding Theorem
information generation.

The theorem provides the minimum average number of bits required to represent the
source output without any loss of information.
Source Encoding, converts source symbols (sk) to binary codewords (bk). Shorter codes for
frequent symbols, longer for rare symbols (e.g., Morse code).
• Average Codeword Length(L) is average bits per symbol
L =σ pk lk ; pk : Probability of symbol, lk : length of binary codeword for sk.
Efficiency: 𝜂 =
𝐿𝑚𝑖𝑛
𝐿
, 𝜂 ≤ 1
Source Coding Theorem: Entropy H(S) sets the lower bound on L : L ≥ H(S)
Efficient encoding minimizes L to H(S) , achieving maximum compression

Discrete Memoryless Channel
information transmission

In Discrete Memoryless Channel
the current output depends only on
the current input
It is a statistical model with Input
X & Output Y, a noisy version
of X. X and Y are random
variables
Both {X} and {Y} have finite
sizes.

Channel Characteristics
Input Alphabet: X = {x0, x1, …, xJ-1}
Output Alphabet: Y = {y0, y1, …, yK-1}
Transition Probabilities
p(yk|xj), 0 ≤ p(yk|xj) ≤ 1,
σ𝑘 p(yk|xj) = 1
Channel Matrix ( P )
EXAMPLE 5 Binary Symmetric Channel
Probability Distributions
1. Input Distribution:
p(xj) , the probability of input xj
2. Joint Distribution:
p(xj,yk)=p(yk|xj)p(xj)
3. Output Distribution:
P(yk)= σ𝑗=0
𝐽−1
p(xj,yk)=p(yk|xj)p(xj)

Conditional Entropy, H(X|Y)
Measures the remaining uncertainty about the channel
input X , after observing the channel output Y
H(X|Y) = σ𝑘=0
𝐾−1 σ𝑗=0
𝐽−1
p(xj,yk) log2
1
p(xj|yk)
Mutual Information, I(X;Y)
Quantifies the uncertainty about X resolved by
observing Y
I(X;Y) = H(X) - H(X|Y). Or I(Y;X) = H(Y) - H(Y|X)
1. I(X;Y) : Uncertainty in the input resolved by
observing the output.
2. I(Y;X) : Uncertainty in the output resolved by
knowing the input.
Properties of Mutual
Information
1. Symmetry
I(X;Y) = I(Y;X)
2. Non-Negativity
I(X;Y) ≥ 0
3. Relationship with Entropy
I(X;Y) = H(X) + H(Y) - H(X, Y)

Channel capacity C is the maximum reliable information transfer rate for a
communication channel measured in bits per channel use.
Input alphabet X and output alphabet Y. Transition probabilities p(yk|xj) describe the
channel’s behavior.
➢ Mutual Information Expressed as,
I(X;Y) = σ𝑘=0
𝐾−1 σ𝑗=0
𝐽−1
p(xj,yk) log2
𝑝(𝑦𝑘|𝑥𝑗)
p(yk)
Indicates the amount of information transmitted between input and output
➢ Joint and Marginal Probabilities:
p(xj,yk) = p(yk|xj)p(xj) (joint probability).
P(yk) = σ𝑗=0
𝐽−1
p(yk|xj) p(xj) (marginal probability).

Channel Capacity C= max{p(xj)} I(X;Y)
Maximization is performed over all input probability distributions
Input Probability Constraints
p(xj0 ≥ 0 for all j. σ𝑗=0
𝐽−1
𝑝 𝑥𝑗 = 1
Reflects the channel’s intrinsic ability to transmit information.
Independent of the specific input distribution.
Significance:
Represents the theoretical upper limit for reliable communication over the channel.
Forms the basis for Shannon’s Channel-Coding Theorem.

➢ Channel Coding combat noise in digital communication channels and
ensure reliable data transmission.
➢ Add controlled redundancy to reduce errors and improve reliability.
➢ Channel Encoder Maps input data to a coded sequence.
➢ Channel Decoder Reconstructs original data from received signals.

Block Codes
➢Input data is divided into blocks of k bits.
➢Each k -bit block is encoded into an n -bit block ( n > k ).
➢Code Rate, r =
𝑘
𝑛
, where r < 1 .
Shannon’s Theorem
➢ If
𝐻(𝑆)
𝐶
≤
𝑇𝑐
𝑇𝑠
,
➢ then data can be transmitted with arbitrarily low error probability using a
suitable coding scheme.
➢ If
𝐻(𝑆)
𝐶
>
𝑇𝑐
𝑇𝑠
, error-free reconstruction is impossible.
➢ Critical Rate
𝐶
𝑇𝑐
is the maximum reliable transmission rate.
Tc : channel transmission time, Ts : sampling time

Limitations
➢The theorem proves good codes exist but doesn’t show how to construct them.
➢It doesn’t give exact error probabilities but states they tend to zero as code length
increases.
Binary Symmetric Channels
➢For a binary source with entropy 1 bit per symbol, and encoder rate r =
𝑇𝑐
𝑇𝑠
➢Reliable transmission is possible if r ≤ C (code rate ≤ channel capacity).

Introduction to Algebra
Groups

A group is a set with a binary
operation satisfying:
1. Closure: a*b ∈ 𝐺
2. Associativity: a*(b*c) = (a*b)*c
3. Identity Element:
e ∈ G such that a*e =e*a =a
1. Inverse Element: For each
a ∈ G, ത
𝑎 ∈ G such that a*ത
𝑎 = 𝑒
1. Commutative Group: a*b = b*a
Theorems:
1. Unique Identity: Only one identity
element e exists.
2. Unique Inverse: Each element a has only
one inverse.
Examples:
1. Integers under Addition: Identity: 0,
Inverse: -i
2. Rational Numbers (excluding 0) under
Multiplication: Identity: 1 , Inverse:
𝒃
𝒂
Example 2.1, Example 2.2, Example 2.3
(TEXT 1)

A field is a set where addition, subtraction,
multiplication, and division (except by 0) are possible
without leaving the set. These operations follow
commutative, associative, and distributive laws.(GF)
Definition of a Field
A set F with operations + (addition) and .
(multiplication) is a field if:
➢ Additive Group: forms a commutative group
under addition with identity 0 .
➢ Multiplicative Group: Nonzero elements of F
form a commutative group under multiplication
with identity 1.
➢ Distributive Law: a.(b+c) = a.b + a.c
Key Properties
1. a.0=0
2. Nonzero elements are closed
under multiplication.
3. a.b =0 implies a = 0 or b = 0
4. – (a.b) = (-a) . b = a.(-b)
5. If a≠ 𝟎,
𝒂. 𝒃 = 𝒂. 𝒄 𝒊𝒎𝒑𝒍𝒊𝒆𝒔 𝒃 = 𝒄
Examples
1. Real Numbers: A field with
infinite elements.
2. Finite Fields: Fields with a
limited number of elements exist
and are discussed later.

Galois Fields (GF)
➢ Codes can be constructed from any Galois field GF(q) , where q is either a
prime p or a power of p .
➢ Binary fields GF(2) and their extensions GF(2n) are particularly important for digital
data transmission and storage because binary coding is practical and universal.
Binary Arithmetic in GF(2)
➢ Arithmetic uses modulo-2 operations:
• Addition: 1 + 1 = 0 (since 2 = 0 in modulo-2).
• Subtraction is the same as addition because 1 = -1 .
Example equations: x + y = 1, x + z = 0, x+y+z =1. By solving, z = 0 , x = 0 , and y = 1 .
Linear Independence of Equations
➢ The equations are linearly independent, confirmed by the determinant of coefficients
being nonzero.

Definition of a Polynomial Over GF(2) : A polynomial f(X) has the form:
f(X) = f0 + f1X + f2X2 + …. + fnXn, fi ∈ {0, 1}
➢ Degree: Largest power of X with a nonzero coefficient.
➢ Total: 2n polynomials for degree n .
2. Key Operations: Addition/Subtraction
→ Coefficients for each power of X are added modulo-2.
Example:
a(X) = 1+X+X3+X5, b(X) = 1+X2+X3+X4+X7
a(X)+b(X) = X+X2+X4 +X5+X7

Multiplication:
Multiply like regular
polynomials but use
modulo-2 addition
for combining terms.
Example: multiply
f(X) and g(X)

Construction of Galois Fields GF (2m) and its properties
(Only statements of theorems without proof)

➢ Galois fields are critical in coding theory, cryptography, and digital communications.
➢ They enable error detection and correction (e.g., Reed-Solomon codes).
➢ Used in designing secure cryptographic systems (e.g., AES encryption).

Construction GF(2m) of from GF(2)
1. Start with two elements and from GF(2) and introduce a new symbol ∝
2. Define a multiplication operation “.” such that:
➢ Basic rules: 0, ∝ j = ∝ j.0 = 0, and 1. ∝ j = ∝ j.1 = ∝ j
➢ Closure: Multiplication wraps around using the condition ∝ 2m-1 = 1.
3. Primitive Polynomial: Choose a primitive polynomial p(X) of degree m over
GF(2) such that p(∝)=0. This ensures the field has exactly 2m elements.

4. Field Elements
➢ The elements are 0,1, ∝, ∝ 2,,….., ∝ 2m-2
➢ Nonzero elements {1, ∝, ∝ 2,,….., ∝ 2m-2 }form a commutative group under
multiplication
5. Addition
➢ Polynomials of degree m-1 over GF(2) represent the field elements.
➢ Addition is performed using modulo-2 addition of polynomial coefficients
6. Representations
➢ Power Representation: ∝i, for i= 0,1, …., 2m-2
➢ Polynomial Representation: Elements expressed as polynomials of ∝ with degree < m.
➢ Tuple Representation: Coefficients of the polynomial form a binary m -tuple.

7. Example
➢Primitive polynomial p(X) = 1+X+X4
➢Closure: ∝ 4 = 1 + ∝
➢Elements { 0, 1, ∝, ∝ 2, ∝3, 1+ ∝, ∝ + ∝ 2, 1+ ∝ + ∝ 2+ ∝ 3 }
➢Multiplication and addition follow modulo-2 rules.
8. Properties
➢GF(2m) is a field with characteristic 2.
➢Addition and multiplication are associative, commutative, and distributive.
➢GF(2) is a subfield of GF(2m)

Galois Fields GF (2m) Properties

The mathematical properties of Galois fields (GF) over binary finite fields. It
highlights foundational theorems, examples, and computational methods for
understanding the structures and behaviours within these fields.
1. Extension Fields
➢Polynomials over GF(2) may not have roots within GF(2), but their
roots exist in an extended field GF(2m)
Example: The polynomial X4+ X3+ 1 has roots ∝ 1, ∝ 2, ∝ 3 , ∝ 4 in GF(24)
2. Conjugates and Roots
➢If 𝛽 is a root of f(X) in GF(2m), all its conjugates 𝛽2𝑖
(for i≥ 0 ) are
also roots

3. Minimal Polynomials
➢The smallest degree polynomial 𝜙 𝑋 over GF(2) such that 𝜙 𝛽 = 0
is called the minimal polynomial of 𝛽
➢ Minimal polynomials are
• Unique for each element
• Irreducible over GF(2)
Example: For 𝛽 =∝ 3 in GF(24), 𝜙 𝑋 = X4 + X3 + X2 + X + 1

4. Roots of Polynomials
➢Theorem 2.8: The 2m - 1 nonzero elements of GF(2m) are roots of 𝑋2𝑚
+1
➢Corollary 2.8.1: The elements of GF(2m) form all roots of 𝑋2𝑚
+ X
5. Primitive Elements
➢A primitive element ∝ generates all nonzero elements of GF(2m) through its powers.
➢All conjugates of a primitive element are also primitive.
Example: Generetae GF(23), f(x)= x3+x+1 ( irreducible )

6. Irreducibility
➢ An irreducible polynomial is a polynomial that cannot be factored into smaller
polynomials over GF(2). Ex: f(x) = x3 + x+ 1 cannot be factored further modulo 2.
➢Theorems provide the criteria for irreducibility of polynomials over GF(2) and their
role in constructing GF(2m)
Ex: f(x) = x3 + x+ 1 cannot be factored further modulo 2.
Verifying irreducibility by checking f(∝) ≠ 0 for all ∝ ∈ GF(2)
For x = 0, f(0) = 1
For x = 1, f(1) = 1 + 1 + 1 = 1
Thus, f(x) is irreducible.

Example 2.9
✓ Considers the finite field GF(2⁴) and shows how the powers of 𝜷 = ∝3 generate all
nonzero elements.
✓ Demonstrates that conjugates of 𝜷 are also primitive.
Theorem 2.17
✓ If 𝜷 is an element of order m in GF(2ⁿ), then all its conjugates have the same order.
Example 2.10
✓ Illustrates that an element ∝ 3 in GF(2⁴) has a minimal polynomial x4 + x + 1 ,
whose roots (conjugates) have the same order 4.

Primitive Elements and Conjugates in GF(2ⁿ)
1. Primitive Elements
✓ If 𝜷 is a primitive element of GF(2ⁿ), all its conjugates (e.g., 𝛽 2, 𝛽 4,
𝛽 8, … ) are also primitive elements.
✓ The order of 𝛽 is 2n - 1 , meaning it generates all nonzero elements of
GF(2ⁿ).
2. Theorem 2.16
✓ If 𝛽 is a primitive element of GF(2ⁿ), then all its conjugates 𝛽 2, 𝛽 4,
𝛽 8, … are also primitive elements.

Computation Using Galois Field GF (2m) Arithmetic
Example computations using arithmetic over GF(2ⁿ).
1. X + ∝Y = ∝ 3
2. ∝ X + ∝ 7 Y = ∝ 5

Vector spaces and Matrices (Chap. 2 of Text 2).

A vector space is a set of elements (vectors) with defined vector addition and
scalar multiplication
Vector spaces are defined over a field (F), which contains scalars (real numbers, complex
numbers, etc.). Used in mathematics, physics, and engineering for solving linear equations,
transformations, and coding theory.
A set V is called a vector space over a field F if it satisfies:
1. Closure under Addition & Scalar Multiplication
2. Commutative & Associative Properties
3. Distributive Laws
4. Existence of Additive Identity (0)
5. Existence of Additive Inverse
6. Multiplication by Scalar Identity: 1.v =v

Basic Properties
1. Zero Scalar Property: 0.v = 0
2. Zero Vector Property: c.0 = 0
3. Negative Scalar Multiplication: (-c).v = c.(-v) = - (c,v)
Vector Space over GF(2)
1. A vector space can be formed over the binary field GF(2) where elements
are 0 and 1.
2. Vector addition is done using modulo-2 addition (XOR operation).
3. Scalar multiplication follows modulo-2 multiplication.(AND operation)

Subspaces of a Vector Space
A subset S of a vector space V is a subspace if:
1. It is non-empty (contains the zero vector).
2. Closed under addition: If u, v ∈ S, then u + v ∈ S.
3. Closed under scalar multiplication: If a ∈ F and v ∈ S, then a . v ∈ S.
Example:
✓ Consider V5, the vector space of 5-tuples over GF(2).
✓ The set S = {(0 0 0 0 0), (0 0 1 1 1), (1 1 0 1 0), (1 1 1 0 1)} is a subspace.

Linear Combination & Span
A vector w is a linear combination of v1, v2, …, vk
If, w = a1 v1 + a2 v2 + … + ak vk. → where a1, a2, …, ak are scalars.
The span of a set of vectors is the set of all possible linear combinations of those vectors. In
other words, it is the collection of all vectors that can be created by adding and scaling the
given vectors.
Example:
Consider the set { (0 0 1 1 1), (1 1 1 0 1) } in V5.
The four possible linear combinations form a subspace.

Linear Independence & Basis
Linearly Independent Set: Vectors v1, v2, …, vk are linearly independent if ,
a1 v1 + a2 v2 + … + ak vk. = 0 → only when all scalars a1, a2, …, ak are zero.
If at least one scalar is nonzero, the vectors are linearly dependent.
A basis of a vector space is a set of linearly independent vectors that span the space.
The number of basis vectors is called the dimension of the vector space.
Example:
The set {(1 0 1 1 0), (0 1 0 0 1), (1 1 0 1 1)} is linearly independent.
It forms a basis for a subspace of V5.

Generalization to GF(q)
The above concepts extend to matrices over GF (q) where
q = pm (power of a prime).

Module 2
Linear block codes: Generator and parity check matrices,
Encoding circuits, Syndrome and error detection,
Minimum distance considerations, Error detecting and error
correcting capabilities, Standard array and
syndrome decoding, Single Parity Check Codes (SPC),Repetition
codes, Self dual codes, Hamming codes,
Reed-Muller codes. Product codes and Interleaved codes(Chap. 3
of Text 2).
Done by supriya

Linear Block Codes: Generator
and Parity Check Matrices:
1. Input Parameters (Message
length k, Codeword length n, and
Generator matrix G)
2. Encoding Process (Generating
codewords using c = mG)
3. Parity Check Matrix H
Calculation (Finding the relation
between G and H)
4. Syndrome Calculation for
Error Detection

Encoding Circuits for Linear
Block Codes:
1. Input Parameters (Message
bits m, Generator matrix G)
2. Matrix Multiplication (c = mG
for encoding)
3. Modulo-2 Addition (Binary
addition without carry)
4. Output the Codeword c

Syndrome and Error Detection
in Linear Block Codes:
1. Input Received Codeword r
2. Calculate Syndrome S = HrT
Using Parity Check Matrix H
3. Check if Syndrome S is Zero
➢ If S = 0 → No Error
Detected, Output Codeword
➢ If S neq 0 → Error
Detected, Locate and Correct
Error

Minimum Distance Considerations in
Linear Block Codes:
1. Input Codewords (Set of valid
codewords)
2. Compute Hamming Distance (Pairwise
distance between codewords)
3. Find Minimum Distance dmin
(Smallest nonzero Hamming distance)
4. Determine Error Detection &
Correction Capability
➢ t = [ (dmin - 1) / 2 ] (Error correction
capability)
➢ dmin - 1(Error detection capability)

Error Detecting and Error Correcting
Capabilities in Linear Block Codes:
1. Input Codewords and Minimum Distance dmin
2. Calculate Error Detection Capability (dmin - 1)
3. Calculate Error Correction Capability
(t = [(dmin - 1) / 2 ]
4. Determine System Capability
➢ If t is sufficient → Correct errors
➢ If not → Only detect errors

• Standard Array and Syndrome Decoding:
• Input Received Codeword
• Compute Syndrome S = HrT
• Using Parity Check Matrix H
• Check Standard Array for Error Pattern
• Correct the Codeword Using Nearest
Valid Codeword
• Output Corrected Codeword

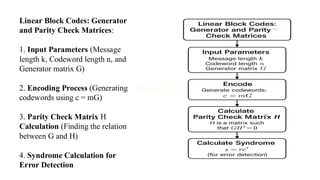
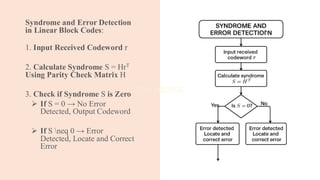
Single Parity Check (SPC) Codes with
important equations.
1. Input Message Bits : m
2. Compute Parity Bit p Using:
p = m1 ⊕ m2 ⊕ …. ⊕ mk
(Where ⊕ is XOR operation)
3. Generate Codeword c = [m, p]
4. Transmit Codeword
5. At Receiver: Compute Syndrome S
S = c1 ⊕ c2 ⊕ …. ⊕ cn
6. Check for Errors:
➢ If S = 0, No Error.
➢ If S ≠ 0, Error Detected
(SPC can only detect single-bit errors).

ECC module 1 & 2 SLIDESHARE_watermark.pdf

More Related Content

Similar to ECC module 1 & 2 SLIDESHARE_watermark.pdf

More from T.D. Shashikala

Recently uploaded

ECC module 1 & 2 SLIDESHARE_watermark.pdf