This document provides an overview of information theory and coding concepts including: 1) Definitions of information, entropy, joint entropy, conditional entropy, and mutual information are introduced along with examples of calculating these quantities for discrete memoryless sources and channels. 2) Shannon's theorem for channel capacity is discussed and the channel capacity of a discrete memoryless channel is defined as the maximum mutual information over all possible input distributions. 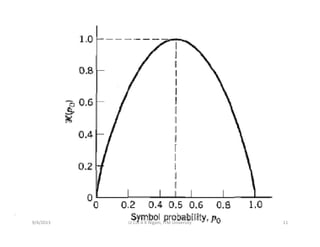3) Properties of entropy such as it being a measure of uncertainty, having a minimum of 0 and maximum of log2K, and being maximized when probabilities are equal are proven.

1. Unit 2
Information Theory and CodingInformation Theory and Coding
By
Prof A K Nigam
9/4/2013 1Lt Col A K Nigam, ITM University

2. Syllabus for Unit 2
• Definition of information
• Concept of entropy• Concept of entropy
• Shannon’s theorem for channel capacity
• Shannon‐Hartley theorem
• Shannon channel capacityp y
(Reference Book Communication Systems 4Th Edition Simon Haykin)

3. Definition of information
We define the amount of information gained after observing
th t S hi h ith d fi d b bilit ththe event S which occurs with a defined probability as the
logarithmic function
( )
1
logk
k
I s
p
⎛ ⎞
⎜ ⎟
⎝ ⎠k
k k
p
Where p is probabilityof occuranceof event s
⎝ ⎠
Remember
Joint Probability P(x, Y)
di i l b biliConditional Probability
P(A/B)= Pr. Of occurrence of A after B has occurred)

4. Important properties
• If we are absolutely certain of the outcome of an
event, even before it occurs, there is no information
gained.gained.
•The occurrence of an event either provides some or no
information but never brings about a loss ofinformation, but never brings about a loss of
information.
•The less probable an event is, the more information we
gain when it occurs.
•If sk and sl are statistically independent.
9/4/2013 4Lt Col A K Nigam, ITM University

5. Standard Practice for defining informationStandard Practice for defining information
• It is the standard practice today to use a logarithm to base 2.p y g
The resulting unit of information is called the bit
• When pk = 1/2, we have I(sk) = 1 bit. Hence, one bit is theWhen pk 1/2, we have I(sk) 1 bit. Hence, one bit is the
amount of information that we gain when one of two
possible and equally likely events occurs.
9/4/2013 5Lt Col A K Nigam, ITM University

6. Entropy of a discrete memoryless sourceEntropy of a discrete memoryless source
• Entropy of a discrete memory‐less source with sourcepy f y
alphabet ‘S’ is a measure of the average information content
per source symbol.
9/4/2013 6Lt Col A K Nigam, ITM University

7. Properties of EntropyProperties of Entropy
1. Entropy is a measure of the uncertainty of the randompy y
variable
2. H(s)=0, if and only if the probability p= 1 for some k, and the
remaining probabilities in the set are all zero; this lower
bound on entropy corresponds to no uncertainty.py p y
3. H(s)= log2K, if and only if pk = 1/K for all k (i.e., all the
symbols in the alphabet Y are equi‐probable); this upper
bound on entropy corresponds to maximum uncertainty.
9/4/2013 7Lt Col A K Nigam, ITM University

8. Proof of these properties of H(s)Proof of these properties of H(s)
2nd Property
• Since each probability pk is less than or equal to unity, it
follows that each term pk Iog2(1/pk) is always nonnegativefollows that each term pk Iog2(1/pk) is always nonnegative,
and so H(s) ≥ 0.
• Next, we note that the product term pk Iog2(1/pk) is zero if,
and only if pk = 0 or 1.
• We therefore deduce that H(s) = 0 if, and only if pk= 0 or 1,
that is pk = 1 for some k and all the rest are zero.
9/4/2013 8Lt Col A K Nigam, ITM University

9. Example: Entropy of Binary Memoryless Source
• We consider a binary source for which symbol 0 occurs• We consider a binary source for which symbol 0 occurs
with probability P(0) and symbol 1 with probability P(1) =
1 – P(0) We assume that the source is memory-less
• The entropy of such a source equals
H(s) = - P(0) log2 P(o) - P(1) log2 P(1)
= - P(o) log2 P(o) - {1 – P(o)} log2{l – P(o)} bits
• For P(0)=0 P(1)=1 and thus H(s)=0
• For P(0)=1 P(1)=0 and thus H(s)=0
• For P(0)=P(1)=1/2 it is maximum=1
9/4/2013 9Lt Col A K Nigam, ITM University

10. 2 2log (1 )log (1 )
{ l l (1 ) l (1 )}
H p p p p
dH d
= + − −
2 2 2{ log log (1 ) .log (1 )}
1
log loga a
p p p p p
dp dp
d
weknowthat x e thus wecan write
dx x
= − + − − −
=
2 2 2 2 2
1 1
{log . log log ( 1) log ( 1) log (1 )}
1 1
1
dx x
dH p
p p e e e p
dp p p p
= − + + − − − − −
− −
2 2 2 2
1
{log log ( 1)log log (1
1
p e p e
p
= − + + − − −
−
2 2 2 2
)
{log log log log (1 )}
p
p e e p= − + − − −
2 2
2 2
{log log (1 )} 0
log log (1 )
(1 ) 5
p p
p p
or p P p
= − − − =
⇒ = −
= − ⇒ =
2 2
(1 ) .5
1 1
( ) log 2 log 2 1
2 2
max max
or p P p
Entropy isthus H s
Thus Entropyis whenthe probabilities areequal andwecan write valueof
= ⇒ =
= + =
max
max maxThus Entropyis whenthe probabilities areequal andwecan write valueof
Entropy H p= =
1
1 1
log log /
M
k
k k
M M bits Message
p M=
⎛ ⎞
= =⎜ ⎟
⎝ ⎠
∑9/4/2013 10Lt Col A K Nigam, ITM University

11. 9/4/2013 11Lt Col A K Nigam, ITM University

12. Proof of 3rd statement:Condition for Maximum Entropy
• We know that the entropy can achieve maximum value of
log2 M where M is the number of symbols.
If th t ll b l i b bl th• If we assume that all symbols are equiprobable then
probability of each occurring is 1/M
• The associated entropy is thereforepy
2
1
1
( ) log
M
k
k k
H s p
p=
= ∑
2
1 1
. log
1/
k kp
M
M M
=
• This is maximum value of entropy and thus it is maximum
2log M=
• This is maximum value of entropy and thus it is maximum
when all symbols have equal probability of occurrence
9/4/2013 12Lt Col A K Nigam, ITM University

13. EXAMPLE: Entropy of Source
9/4/2013 13Lt Col A K Nigam, ITM University

14. EXAMPLE: Entropy of SourceEXAMPLE: Entropy of Source
• Six messages with probabilities 0 30 0 25Six messages with probabilities 0.30, 0.25,
0.15, 0.12, 0.10, and 0.08, respectively are
transmitted Find the entropytransmitted. Find the entropy
2 2 2 2 2 2( ) (.30log .30 .25log .25 .15log .15 .12log .12 .10log .10 .08log .08)H x = − + + + + +
10 10 10 10 10 10
1
(.30log .30 .25log .25 .15log .15 .12log .12 .10log .10 .08log .08)
.301
1
.7292
= − + + + + +
= + ×
.301
2.422644= +
9/4/2013 14Lt Col A K Nigam, ITM University

15. Discrete Memoryless Channel
• A discrete memory‐less channel is a statistical model with an
input X and an output Y that is a noisy version of X; both X
and Y are random variables.
9/4/2013 15Lt Col A K Nigam, ITM University

16. Channel matrix, or transition matrix
A convenient way of describing a discrete memory-less
channel is to arrange the various transition probabilities ofg p
the channel in the form of a matrix as follows:
9/4/2013 16Lt Col A K Nigam, ITM University

17. Joint EntropyJoint Entropy
• Joint Entropy is defined asJoint Entropy is defined as
( )
1
( )l
m n
∑∑H(XY)= 2
1 1
1
( , )log
( , )
j k
j k j k
p x y
p x y= =
∑∑
= 2( )log ( )
m n
k kp x y p x y−∑∑ 2
1 1
( , )log ( , )j k j k
j k
p x y p x y
= =
∑∑
9/4/2013 17Lt Col A K Nigam, ITM University

18. Conditional EntropyConditional Entropy
• The quantity H(x/y) is called a conditional entropyThe quantity H(x/y) is called a conditional entropy.
• It represents the amount of uncertainty remaining
about the channel input after the channel output
has been observed and is given by:‐
• H(x/y)• H(x/y)
• Similarly H(y/x) can be computed which is averageSimilarly H(y/x) can be computed which is average
uncertainty of the channel output given that x was
transmitted.
9/4/2013 18Lt Col A K Nigam, ITM University

19. Conditional Entropy: ProofConditional Entropy: Proof
• Conditional probability is defined asp y
( , )
( / )
( )
p x y
p x y
p y
• If received symbol is yk
( )p y
m
1
( , )
( / )
( )
m
j k
j
k
k
p x y
then p X y
p y
=
=
∑
• The associated entropy is therefore can be computed as
( )kp y
9/4/2013 19Lt Col A K Nigam, ITM University

20. 2
1
( , ) ( , )
( / ) log
( ) ( )
n
j k j k
k
j k k
p x y p x y
H X y k k
p y p y=
= − ∑
2
1
( / )log ( / )............(1)
n
j k j k
j
p x y p x y
=
= −∑
___________________
( / ) ( / )
Taking average for all valuesof k
H X Y H X yk
=
1
( / ) ( /
( ) ( / )
)
n
k k
k
H X Y H X yk
p y H X y
=
= ∑1
2
1 1
( ) ( / )log (
k
n n
k j k j
k j
p y p x y p x
=
= =
= −∑ ∑ / )ky
1 1k j
2
1 1
( ) ( / )log ( / )
n n
k j k j k
k j
p y p x y p x y
= =
= −∑∑
2
1 1
( , )log ( / )
j
n n
j k j k
k j
p x y p x y
= =
= −∑∑9/4/2013 20Lt Col A K Nigam, ITM University

21. Mutual Information
Problem statement
Mutual Information
Given that we the channel output yk is as a noisy version of the
channel input Xj.
Given that the entropy H(X) is a measure of the prior uncertaintyGiven that the entropy H(X) is a measure of the prior uncertainty
about X, how can we measure the uncertainty about X after
observing Y?

22. Mutual Information Defined
• Note that the entropy H(x) represents our uncertainty about the
channel input before observing the channel output, and the
conditional entropy H(x/y) represents our uncertainty about the
channel input after observing the channel output.
• It follows that the difference H(x) - H(x/y) must represent our( ) ( y) p
uncertainty about the channel input that is resolved by observing
the channel output.
• This important quantity is called the mutual information of the
channel denoted by I(x; y)
• We may thus write I(X; Y)= H(x) - H(x/y) or
= H(y) – H(y/x)
Al it b h th t I(X Y) H( ) +H( ) H( )• Also it can be shown that I(X; Y)= H(x) +H(y)- H(x,y)
9/4/2013 22Lt Col A K Nigam, ITM University

23. Capacity of a Discrete Memoryless Channelp y y
• Channel capacity of a discrete memoryless channel isp y y
defined as the maximum mutual information I(x; y) in any
single use of the channel where the maximization is over all
possible input probability distributions {p(xj)} on Xpossible input probability distributions {p(xj)} on X.
• The channel capacity is commonly denoted by C. We thusp y y y
write
{ ( )}
( ; )maxp x
C I X Y=
• The channel capacity C is measured in bits per channel use,
or bits per transmission
{ ( )}jp x
or bits per transmission.
9/4/2013 23Lt Col A K Nigam, ITM University

24. Examples of Mutual Information Numericalsp
D N i l f Si h d S Ch t• Do Numerical from Singh and Sapre Chapter
10 (10.3.1, 10.4.1, 10.4.2, 10.4.3, 10.5.2,
10 6 2)10.6.2)
9/4/2013 24Lt Col A K Nigam, ITM University

25. Example: Find Mutual Information for the
h l h b lchannel shown below
.8
P(X1)=.6 y1
.2 .3
P(X2)=.4 .7 y2( ) y
.8 .2
( / )P y x
⎡ ⎤
= ⎢ ⎥( / )
.3 .7
P y x ⎢ ⎥
⎣ ⎦
9/4/2013 25Lt Col A K Nigam, ITM University

26. • We know that I(x, y)=H(y)‐H(y/x)……..1
Solution
We know that I(x, y) H(y) H(y/x)……..1
• Finding H(y)
• P(y1)=0.6×0.8+.4×0.3=.6
• P(y2)=0.6×0.2+0.4×0.7=.4
• H(y)=‐3.322× [0.6log0.6+0.4log0.4]=0.971 bits/message
• Finding H(y/x)= ‐
• Finding P(x, y)
( , )log ( / )p x y p y x∑∑
48 12⎡ ⎤
• H(y/x)= ‐3 322[0 48×log0 8+0 12×log0 2+ 0 12×logo 3+0 28×log0 7]
.48 .12
( , )
.12 .28
P x y
⎡ ⎤
= ⎢ ⎥
⎣ ⎦
• H(y/x)= ‐3.322[0.48×log0.8+0.12×log0.2+ 0.12×logo.3+0.28×log0.7]
= 0.7852
• Putting values in 1 we get I(x, y)=0.971‐0.7852=0.1858 bitsg g ( , y)
9/4/2013 26Lt Col A K Nigam, ITM University

27. Types of channels and associated EntropyTypes of channels and associated Entropy
• Lossless channelLossless channel
• Deterministic channel
i l h l• Noiseless channel
• Binary symmetric channel
9/4/2013 27Lt Col A K Nigam, ITM University

28. General Treatment for all the channels
( , ) ( ) ( / ) ........(1)
( ) ( / ) ........(2)
WeknowI x y H x H x y
H y H y x
= −
= −( ) ( / ) ........(2)
( / ) ( )l ( / )
n n
H y H y x
Alsothat
H X Y ∑∑ 2
1 1
( / ) ( , )log ( / )
( , ) ( ) ( / ) ( ) ( / )
j k j k
k j
H X Y p x y p x y
Weknowthat p x y p x p y x p y p x y thuswecanwrite
= =
= −
= =
∑∑
2
1 1
( , ) ( ) ( ) ( ) ( )
( / ) ( ) ( / )log ( / ).
n n
k j k j k
k j
p y p p y p y p y
H X Y p y p x y p x y
= =
= −∑ ∑ .....3
j
( / ) ( ) ( / )log ( / ) 4
n n
Similarlywecanwrite
H Y X p x p y x p y x= ∑ ∑ 2
1 1
( / ) ( ) ( / )log ( / )........4j k j k j
j k
H Y X p x p y x p y x
= =
= −∑ ∑
9/4/2013 28Lt Col A K Nigam, ITM University

29. Lossless channel
• For a lossless channel no source information is lost in
transmission. It has only one non zero element in each
column For examplecolumn. For example
[ ]
3/ 4 1/ 4 0 0 0
( / ) 0 0 1/ 3 2 / 3 0P Y X
⎡ ⎤
⎢ ⎥
⎢ ⎥
• In case of lossless channel p(x/y)=0/1 as the probability of x
[ ]( / ) 0 0 1/ 3 2 / 3 0
0 0 0 0 1
P Y X = ⎢ ⎥
⎢ ⎥⎣ ⎦
• In case of lossless channel p(x/y)=0/1 as the probability of x
given that y has occurred is 0/1
• Putting this in eq 3 we get H(x/y)=0
• Thus from eq. 1 we get
I(x, y)=H(x)
Also C=max H(x)Also C=max H(x)
9/4/2013 29Lt Col A K Nigam, ITM University

30. Deterministic channel
• Channel matrix has only one non zero element in each row, for
example
1 0 0
1 0 0
⎡ ⎤
⎢ ⎥
⎢ ⎥
[ ]
1 0 0
( / ) 0 1 0
0 1 0
0 0 1
P Y X
⎢ ⎥
⎢ ⎥=
⎢ ⎥
⎢ ⎥
⎢ ⎥⎣ ⎦
• In case of Deterministic channel p(y/x)=0/1 as the probability of y
given that x has occurred is 0/1
0 0 1⎢ ⎥⎣ ⎦
• Putting this in eq 3 we get H(y/x)=0
• Thus from eq. 1 we get
I(x, y)=H(y)
Also C=max H(y)
9/4/2013 30Lt Col A K Nigam, ITM University

31. Noiseless channel
• A channel which is both lossless and deterministic, has only one
element in each row and column. For example
1 0 0 0⎡ ⎤
[ ]
1 0 0 0
0 1 0 0
( / )
0 0 1 0
P y x
⎡ ⎤
⎢ ⎥
⎢ ⎥=
⎢ ⎥
• Noiseless channel is both lossless and deterministic thus
H( / ) H( / ) 0
0 0 1 0
0 0 0 1
⎢ ⎥
⎢ ⎥
⎣ ⎦
H(x/y)=H(y/x)=0
• Thus from eq. 1 we get
I(x, y)=H(y)=H(x)
Also C=max H(y)=max H(x)=log2m=log2n where m and n areAlso C=max H(y)=max H(x)=log2m=log2n where m and n are
number of symbols
9/4/2013 31Lt Col A K Nigam, ITM University

32. Binary Symmetric Channel
α (1 )
( / )
p p
X Y
−⎡ ⎤
⎢ ⎥
1‐α
( / )
(1 )
p X Y
p p
=⎢ ⎥−⎣ ⎦
1 α
(1 )p pα α−⎡ ⎤(1 )
( , )
(1 ) (1 )(1 )
p p
p X Y
p p
α α
α α
⎡ ⎤
= ⎢ ⎥− − −⎣ ⎦
9/4/2013 32Lt Col A K Nigam, ITM University

33. 2
1 1
( / ) ( , )log ( / )
n n
j k k j
k j
H Y Y p x y p y x
= =
= −∑∑
( / ) [ (1 )log(1 ) log (1 ) log
putting values frommatrix we get
H Y Y p p p p p pα α α= − − − + + −
(1 )(1 )log(1 )]
[ log (1 )log(1 )]
p p
p p p p
α− − −
= − + − −
.1
( , ) ( ) log (1 )log(1
Putting thisineq we get
I X Y H y p p p= + + − − )p
9/4/2013 33Lt Col A K Nigam, ITM University

34. CHANNEL CAPACITY OF A CONTINUOUS CHANNEL
• For a discrete random variable x the entropy H(x) was defined
as
• H(x) for continuous random variables is obtained by using the
integral instead of discrete summation thus
9/4/2013 34Lt Col A K Nigam, ITM University

35. Similarly
( , ) ( , )log ( , )H X Y p x y p x y dxdy
∞ ∞
−∞ −∞
= − ∫ ∫
( / ) ( , )log ( / )H X Y p x y p x y dxdy
∞ ∞
∞ ∞
−∞ −∞
= − ∫ ∫
( / ) ( , )log ( / )H Y X p x y p y x dxdy
−∞ −∞
∞ ∞
∞ ∞
= − ∫ ∫
( ; )
( ; )
For acontineouschannel I x y is defined as
p x y
−∞ −∞
∞ ∞
∫ ∫
( ; )
( ; ) ( , )
( ) ( )
p x y
I x y p x y dxdy
p x p y−∞ −∞
= − ∫ ∫
9/4/2013 35Lt Col A K Nigam, ITM University

36. Transmission Efficiency of a channelTransmission Efficiency of a channel
Actualtransinformation
M i t i f ti
η =
Maximum transinformation
( ; ) ( ; )I X Y I X Y
= =
max ( ; )I X Y C
Redundancy of a channely
( ; )
1
C I X Y
R η
−
= − =1R
C
η
9/4/2013 36Lt Col A K Nigam, ITM University

37. Information Capacity Theorem for band‐
limited, power‐limited Gaussian channelslimited, power limited Gaussian channels
• Consider X(t) that is band-limited to B hertz.
• Also we assume that uniform sampling of the process X(t)
at the transmitter at Nyquist rate of 2B samples per second
produces 2B samples per second which are to be
transmitted over the channel
• We also know that Mutual Information for a channel is
I(X; Y)=H(y) – H(y/x)=H(x) - H(x/y)….already done( ; ) (y) (y ) ( ) ( y) y
9/4/2013 37Lt Col A K Nigam, ITM University

38. Information Capacity Theorem…….
•For Gaussian channel the probability density is given by
2 21 2 2
/ 2
2
1
( )
2
x
p x e σ
πσ
−
=
•For this p(x), H(x) can be shown to be (not required to be solved)
2 21
( ) log 2 log(2 )H x e eπ σ π σ= =
………….1
•If signal power is S and noise power is N then the received signal is sum of
t itt d i l ith S d i ith N th j i t t
( ) og og( )
2
x e eπ σ π σ
transmitted signal with power S and noise with power N then joint entropy
of the source and noise is
9/4/2013 38Lt Col A K Nigam, ITM University

39. ( , ) ( ) ( / )
( / ) ( )
H x n H x H n x
If thetransmitted signal and noiseareindependent then H n x H n
= +
=( / ) ( )
( , ) ( ) ( )............
If thetransmitted signal and noiseareindependent then H n x H n
Thus
H x n H x H n A= +
signal
( , ) ( , )
Sincethereceived is sumof signal x and noisen wemay equate
H x y H x n=
( , ) ( ) ( / )But H x y H y H x y= + using thisandeq.A weget
( ) ( / ) ( ) ( )
R i hi
H y H x y H x H n+ = +
2
Rearranging this weget
( ) ( / ) ( ) ( ) ..........2
(using ( ) 1
H x H x y H y H n Mutual Information
Now N or S N from Eq we getσ
− = − =
+(using ( ) .1
1
( ) log{2 ( )} ( )
2
Now N or S N from Eq we get
H y e S N y S N
σ
π
= +
= + = +
1
( ) log{2 ( )}
2
and H N e Nπ=
9/4/2013 39Lt Col A K Nigam, ITM University

40. •Putting these values in eq 2 we get
1
( ) l
S N+⎛ ⎞
Putting these values in eq. 2 we get
1
( , ) log
2
1
l
S N
I X Y
N
S
+⎛ ⎞
= ⎜ ⎟
⎝ ⎠
⎛ ⎞1
log 1
2
No.of samplespersecond×MutualInformation
S
N
C
⎛ ⎞
= +⎜ ⎟
⎝ ⎠
= p p
1
2 log 1 log 1
2
S S
B B
N N
⎛ ⎞ ⎛ ⎞
= × + = +⎜ ⎟ ⎜ ⎟
⎝ ⎠ ⎝ ⎠2 N N⎝ ⎠ ⎝ ⎠
(Note: No of samples per sec is 2B as per sampling theorem)(Note: No. of samples per sec is 2B as per sampling theorem)
9/4/2013 40Lt Col A K Nigam, ITM University

41. • With noise spectral density N the total noise in BW B is• With noise spectral density N0 , the total noise in BW B is
spectral density multiplied by BW ie BN0. Thus we can be
write
• This is Shannon theorem for Channel capacity and is used
widely in communication computations.
9/4/2013 41Lt Col A K Nigam, ITM University

42. BW and S/N trade off
0
0 0 0
log 1 log 1
BNS S S
C B
BN N S BN
⎛ ⎞ ⎛ ⎞
= + = +⎜ ⎟ ⎜ ⎟
⎝ ⎠ ⎝ ⎠
0
0
1
/
log 1 log 1
BN
S S BN
S S S S
N BN N BN
⎝ ⎠ ⎝ ⎠
⎛ ⎞ ⎛ ⎞
= + = +⎜ ⎟ ⎜ ⎟
⎝ ⎠ ⎝ ⎠0 0 0 0
1/
(1 )lim
x
N BN N BN
We know that
x e
⎝ ⎠ ⎝ ⎠
+ =
0
1
(1 )lim
x
x e
Thus for
→
+ =
→ ∞B
0
1
/
lim
0 0 0 0
( ) log 1 log 1.44
S BN
B
S S S S
C Max e
N BN N N→∞
⎛ ⎞
= + = =⎜ ⎟
⎝ ⎠
9/4/2013 42Lt Col A K Nigam, ITM University