Downloaded 15 times
Uploaded byFarhana Shaheen
Matrix of linear transformation 1.9-dfs
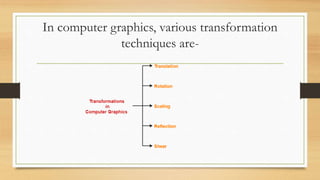
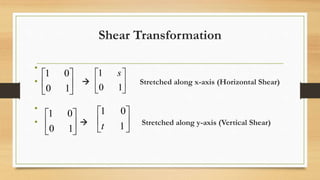
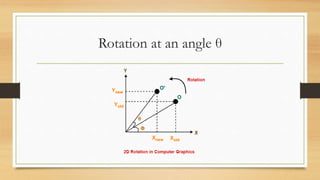
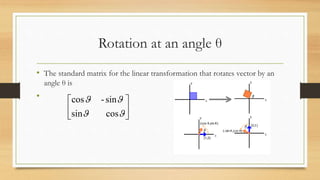
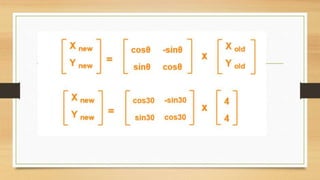
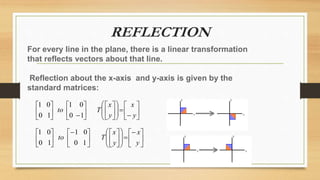
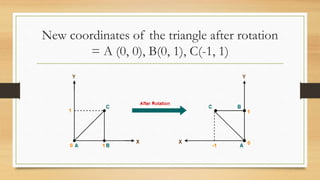
This document discusses various types of linear transformations, including rotations, reflections, shears, dilations, projections, and their representations as matrices. It provides examples of transforming lines and triangles under rotations of different angles. Linear transformations are important in computer graphics for modifying objects by changing their position, size, orientation or shape. Matrix representations allow linear transformations to be described geometrically.
More Related Content
Similar to Matrix of linear transformation 1.9-dfs
More from Farhana Shaheen
Matrix of linear transformation 1.9-dfs
- 1. 1.9 Linear Transformations Dr.Farhana Shaheen
- 2. Objectives: • Learn toview a matrix geometrically as a function. • Learn examples of matrix transformations: reflection, dilation, rotation, shear, projection.
- 3. MATRIX OF LINEAR TRANSFORMTION •Transformation is a process of modifying and re-positioning the existing graphics. • Transformations are helpful in changing the position, size, orientation, shape etc of the object.
- 4. Geometry of LinearTransformations • https://math.hmc.edu/calculus/hmc-mathematics-calculus-online- tutorials/linear-algebra/geometry-of-linear-transformations/
- 5. 2D Transformations • 2DTransformations take place in a two dimensional plane. • 2D Shearing is an ideal technique to change the shape of an existing object in a two dimensional plane.
- 6. In computer graphics,various transformation techniques are-
- 7. Shear Transformation • • Stretched along x-axis (Horizontal Shear) • • Stretched along y-axis (Vertical Shear) 10 01 10 1 s 10 01 1 01 t
- 10. Rotation at anangle θ
- 11. Rotation at anangle θ • The standard matrix for the linear transformation that rotates vector by an angle θ is • cossin sin-cos
- 12.
- 13. Problem-01: Given a linesegment with starting point as (0, 0) and ending point as (4, 4). Apply 30 degree rotation anticlockwise direction on the line segment and find out the new coordinates of the line.
- 15. REFLECTION For every linein the plane, there is a linear transformation that reflects vectors about that line. Reflection about the x-axis and y-axis is given by the standard matrices: y x y x Tto 10 01 10 01 y x y x Tto 10 01 10 01
- 16. Reflection through x-axis •Point in 1st Quadrant will be reflected in 4th Quadrant: y x y x Tto 10 01 10 01
- 17. Reflection through y-axis •Point in 1st Quadrant will be reflected in 2nd Quadrant: y x y x Tto 10 01 10 01
- 18. Reflection through theline y = x • Point in 2nd Quadrant is reflected in 4th Quadrant: x y y x Tto 10 01 10 01
- 19. Reflection through theline y = -x • Point in 1st Quadrant is reflected in 3rd Quadrant: x y y x Tto 01 10 10 01
- 20. Rotation through anangle of -135 degrees then reflected through x-axis
- 21. Problem-02: Given a trianglewith corner coordinates (0, 0), (1, 0) and (1, 1). Rotate the triangle by 90 degree anticlockwise direction and find out the new coordinates.
- 23. New coordinates ofthe triangle after rotation = A (0, 0), B(0, 1), C(-1, 1)
- 24. Expansions and Compressions (Dilationsand Contractions) Given a scalar r, define 22 : RRT by T(x) = rx. T is called a Contraction if 0 < r < 1, and a Dilation if r > 1.
- 25.
- 26.
- 30. Geometry of LinearTransformation • https://math.hmc.edu/calculus/hmc-mathematics-calculus-online- tutorials/linear-algebra/geometry-of-linear-transformations/
- 31. • In thissection we learn to understand matrices geometrically as functions, or transformations. We briefly discuss transformations in general, then specialize to matrix transformations, which are transformations that come from matrices. • https://textbooks.math.gatech.edu/ila/matrix-transformations.html#matrix-trans- matrices-functions • https://www.youtube.com/watch?reload=9&v=kWW6fXV3OKk • LT- Computer Graphics