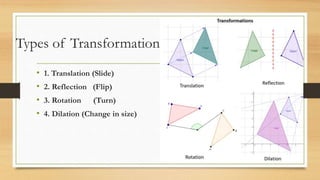
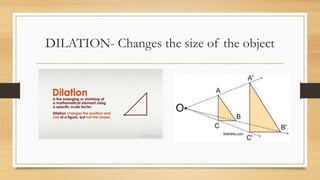
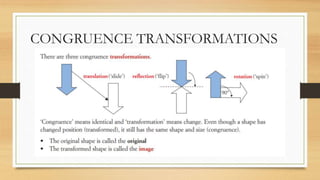
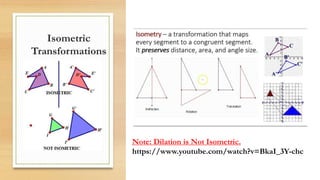
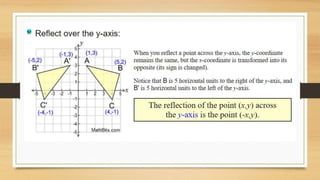
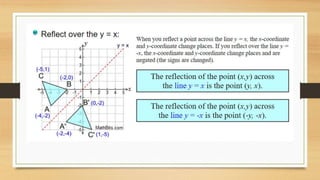
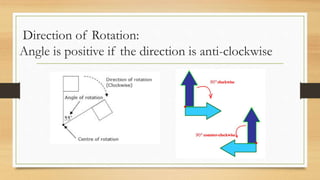
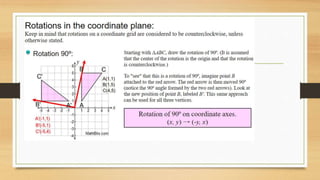
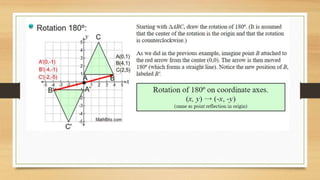
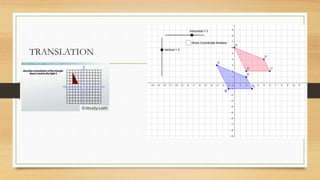
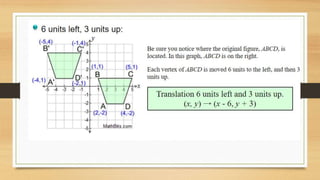
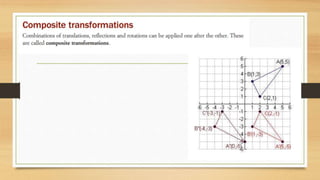
This document discusses different types of geometric transformations including translations, reflections, rotations, and dilations. It provides examples and notations for each type of transformation. Translations involve sliding an object along a vector, reflections involve flipping an object across a line, rotations involve turning an object around a fixed point, and dilations involve changing the size of an object. The document also discusses isometric transformations, lines of reflection, and applications of transformations including tessellations. Examples are provided to demonstrate different transformations and how to find equations of lines of reflection.

1. 9. GEOMETRICAL
TRANSFORMATION
DR. FARHANA SHAHEEN

2. Types of Transformations
• 1. Translation (Slide)
• 2. Reflection (Flip)
• 3. Rotation (Turn)
• 4. Dilation (Change in size)

3. Examples: Types of Transformations

4. Notations:
•Pre-Image
•Image

5. DILATION- Changes the size of the object

6. CONGRUENCE TRANSFORMATIONS

7. Isometric
Transformations
Note: Dilation is Not Isometric.
https://www.youtube.com/watch?v=BkaI_3Y-chc

8. Isometric
Transformations
• Translation (Slide)
• Reflection (Flip)
• Rotation (Turn)

9. Types of
Transformations

11. Types of
Reflection (Flip)
• 1. Reflection by x-axis
• 2. Reflection by y-axis
• 3. Reflection by line y=x
• 4. Reflection by line y=-x
• 5. Reflection by line y=k
• 6. Reflection by line x=k
• 7. Reflection by line y=mx+c

12. Reflection along x- and y-axis

18. Question: 1.
Find the equation of the line of reflection
• 1. Under a reflection, the point P(3,5) is mapped onto the point P’(5,3).
• (i) Find the equation of the line of reflection.
• Sol: If (x, y) ↔ (𝒚, 𝒙), then the equation of line of reflection is y = x.
• (ii) The point P’(5,3) is then reflected and the coordinates of the final
image is P”(-5, 3). Find the equation of the line of the second
reflection.
• Sol: If (x, y) ↔ (−𝒙, 𝒚), then the line of reflection is y-axis, or x = 0.

19. Question: 2.
To find the equation of line of reflection
• The points A and its image A’ is given below. Plot the points, construct
and find the equation of line of reflection in each case.
• (i) A (1, 1), A’(3,1) (ii) A (2, 1), A’(0,3) (iii) A (-1,1), A’(3,-1)
• Hint: Draw the perpendicular bisectors of the line AA’ by drawing arcs
up and down at points A and A’, and joining the points of intersection
of the arcs. This perpendicular bisector will be the line of reflection.
Take any two points on this line, (one can be the midpoint of AA’, and
other can be x- or y-intercepts, or both.

20. • https://mathbitsnotebook.com/Algebra1/FunctionGraphs/FNGTransform
ationRotation.html

21. Example: Rotation (Turn)
Rotation(Turn) ROTATION at an angle of 90 degrees

22. ROTATION
Rotation Point and Angle of
Rotation

23. Rotations:
Centre and Angle of Rotation

24. Direction of Rotation:
Angle is positive if the direction is anti-clockwise

32. Translations in
Tessellations
• Maurits Cornelius Escher (1898 -
1972) is known for his "impossible
drawings", drawings using multiple
vanishing points, and his
"diminishing tessellations". ...
All tessellations can be classified as
those that repeat, are non-periodic,
quasic-periodic, and those that are
fractals.

33. Translations in Tessellations

34. Translation Rules
1. A Translation is Isometric and it preserves orientation.
• 2. We represent a translation, T, of a point A to A’ by T(A).
• A(x,y) → 𝑨′(𝒙 + 𝒂, 𝒚 + 𝒃) is written as T(A) = T(x,y)= (x+a, y+b)
• 3. A translation can also represented by a column vector
𝒂
𝒃
, 𝐬𝐨 𝐭𝐡𝐚𝐭
we have T
𝒙
𝒚 =
𝒙′
𝒚′
=
𝒙
𝒚 +
𝒂
𝒃
=
𝒙 + 𝒂
𝒚 + 𝒃
(Point (a, b) is written as a column vector
𝒂
𝒃
)

35. Example: Translation (Slide- (x,y) → (𝒙 + 𝒂, 𝒚 + 𝒃))

36. TRANSLATION

39. Example: 2

40. Applications of
Geometric
Transformation

41. GeoGebra
• https://www.geogebra.
org/m/k9qvbe7n#mate
rial/dvxpfdxy

42. How to Animate a Transformation
• https://www.youtube.com/watch?v=v9CHlUxnoT8

43. Animation Challenge Roundup:
Transformations!
• https://www.youtube.com/watch?v=21aWtuJanx8