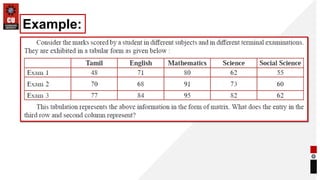
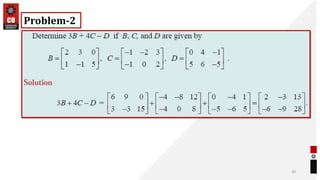
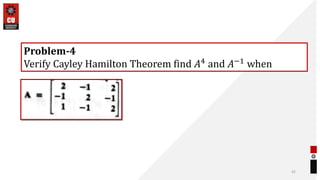
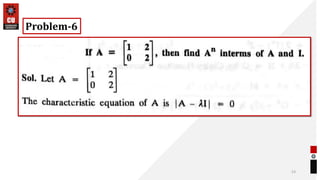
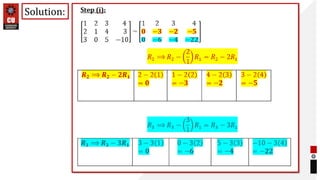
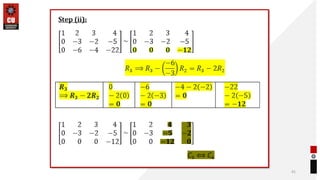
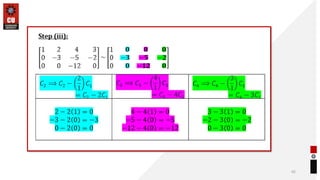
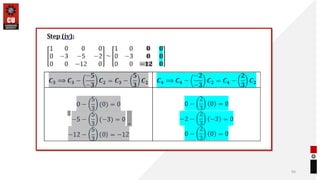
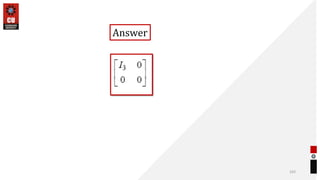
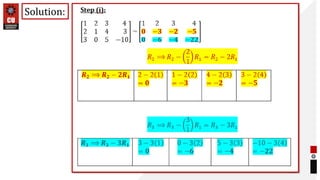
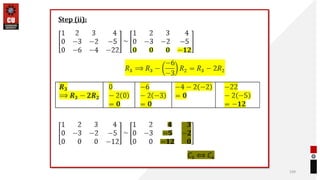
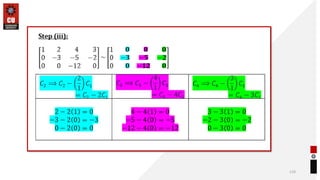
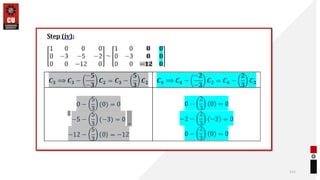
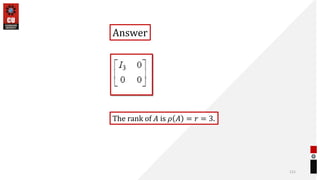
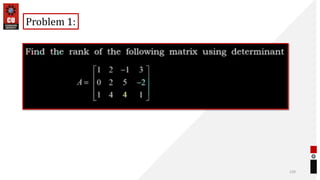
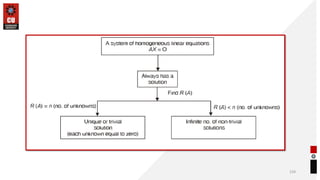
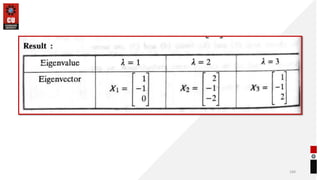
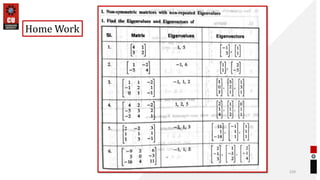
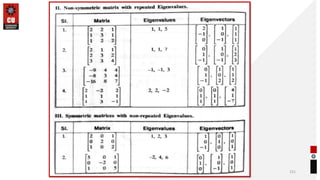
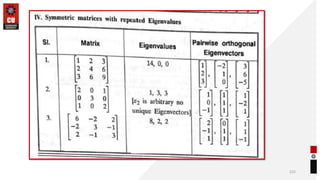
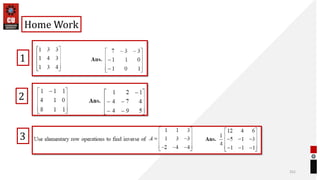
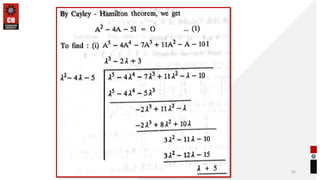This document provides information about matrices and linear algebra concepts. It includes definitions of matrices and their types. It discusses applications of matrices in fields like engineering, technology, cryptography and animation. It also covers topics like matrix operations, elementary transformations, rank of matrices, homogeneous and non-homogeneous equations, eigenvalues and eigenvectors, linear dependence and independence of vectors, and inversion of matrices. Examples and problems are provided for concepts like matrix addition, multiplication, reduction to normal form, and Cayley-Hamilton theorem.




![A matrix is a Rectangular Array (or)
Arrangement of Entries (or) Elements
displayed in Rows and Columns put within a
Square Bracket [ ]
In general, the entries of a matrix may be Real or Complex
Numbers or Functions of one variable (such as Polynomials,
Trigonometric functions or a combination of them) or more
variables or any other object.
Usually, matrices are denoted by CAPITAL LETTERS A, B, C, ... etc
1. Matrices](https://image.slidesharecdn.com/unit-1matricesallthetopics-230821042239-1d081b39/85/UNIT-1-MATRICES-All-the-Topics-pdf-5-320.jpg)