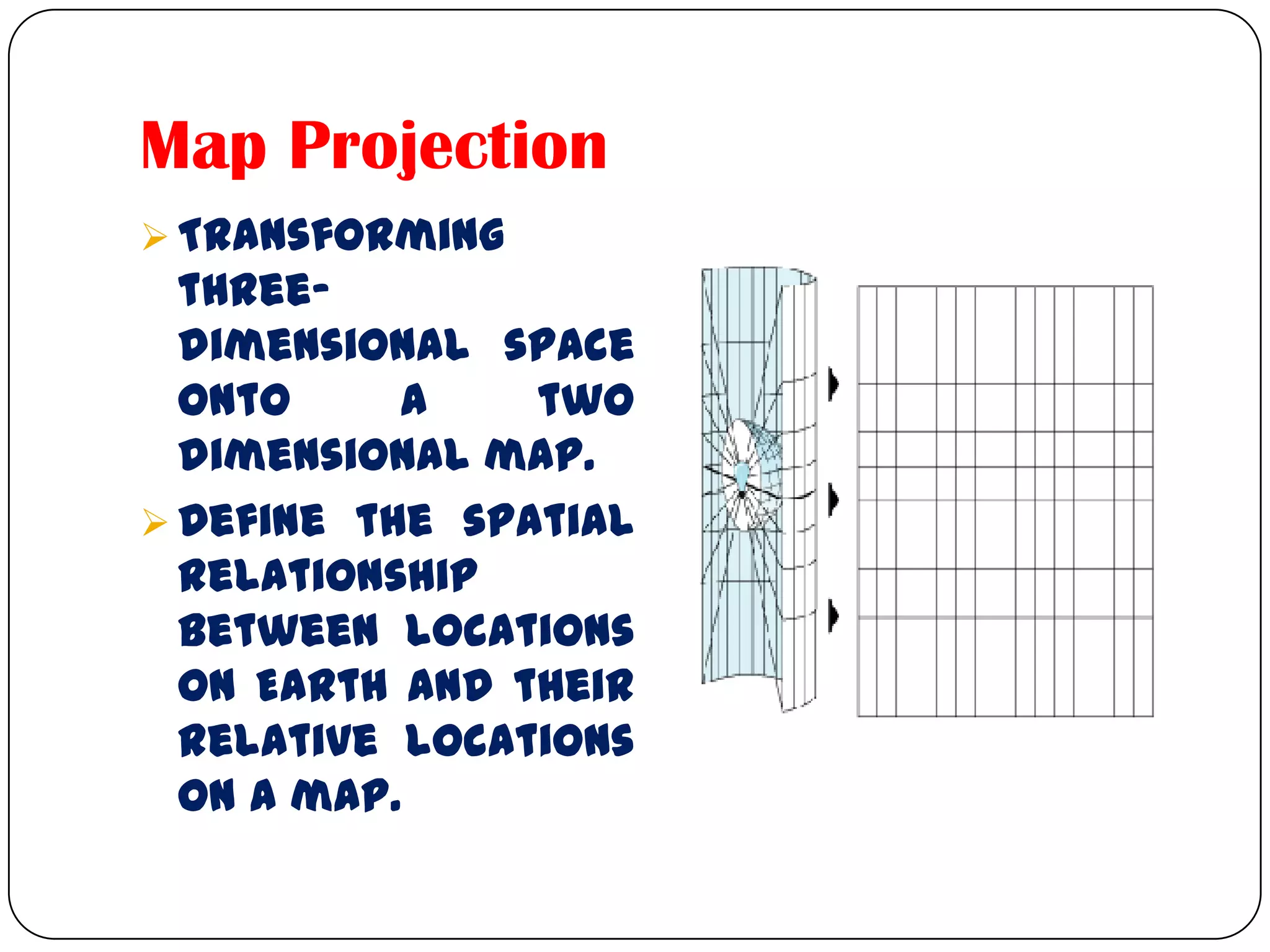
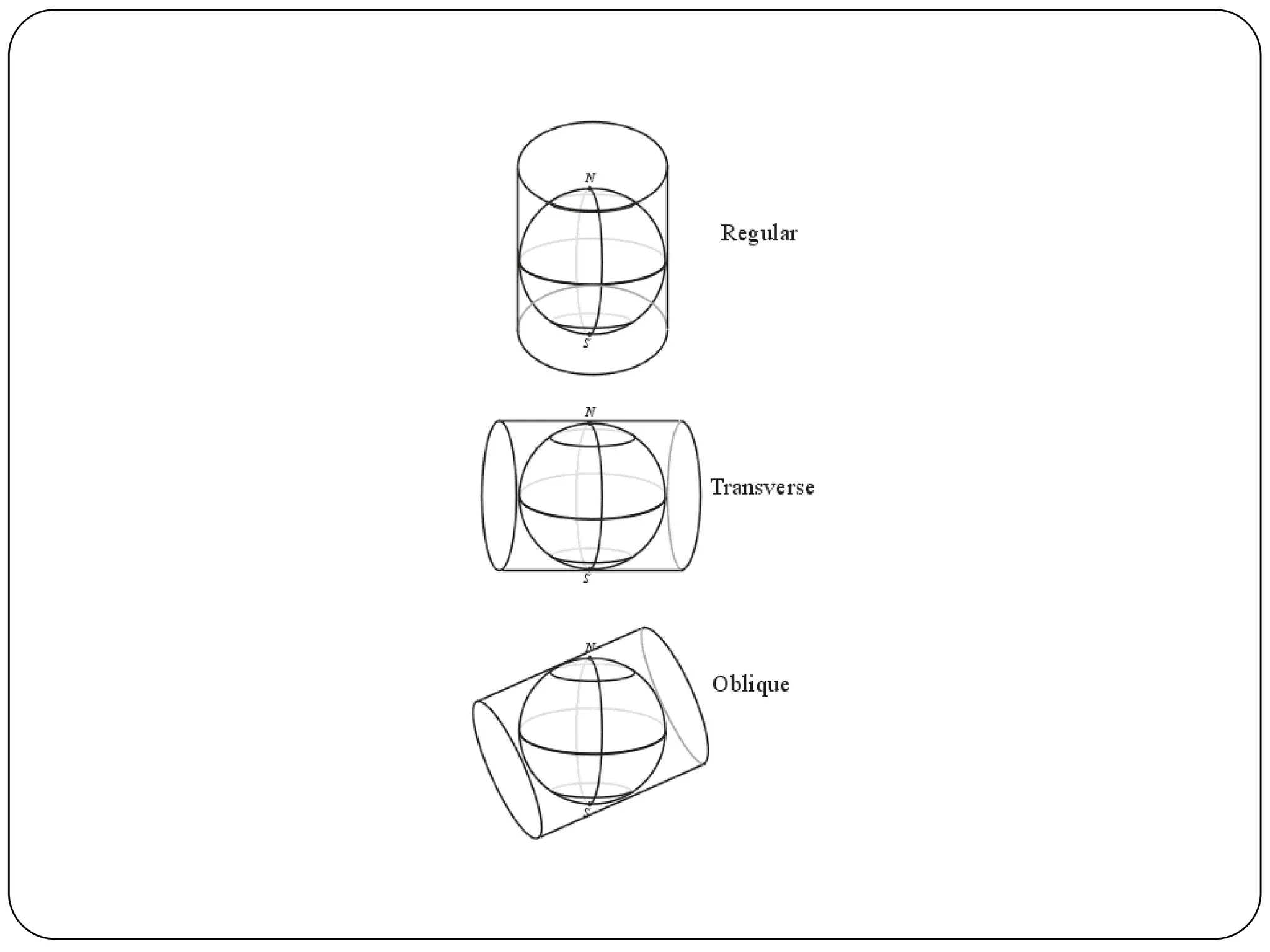
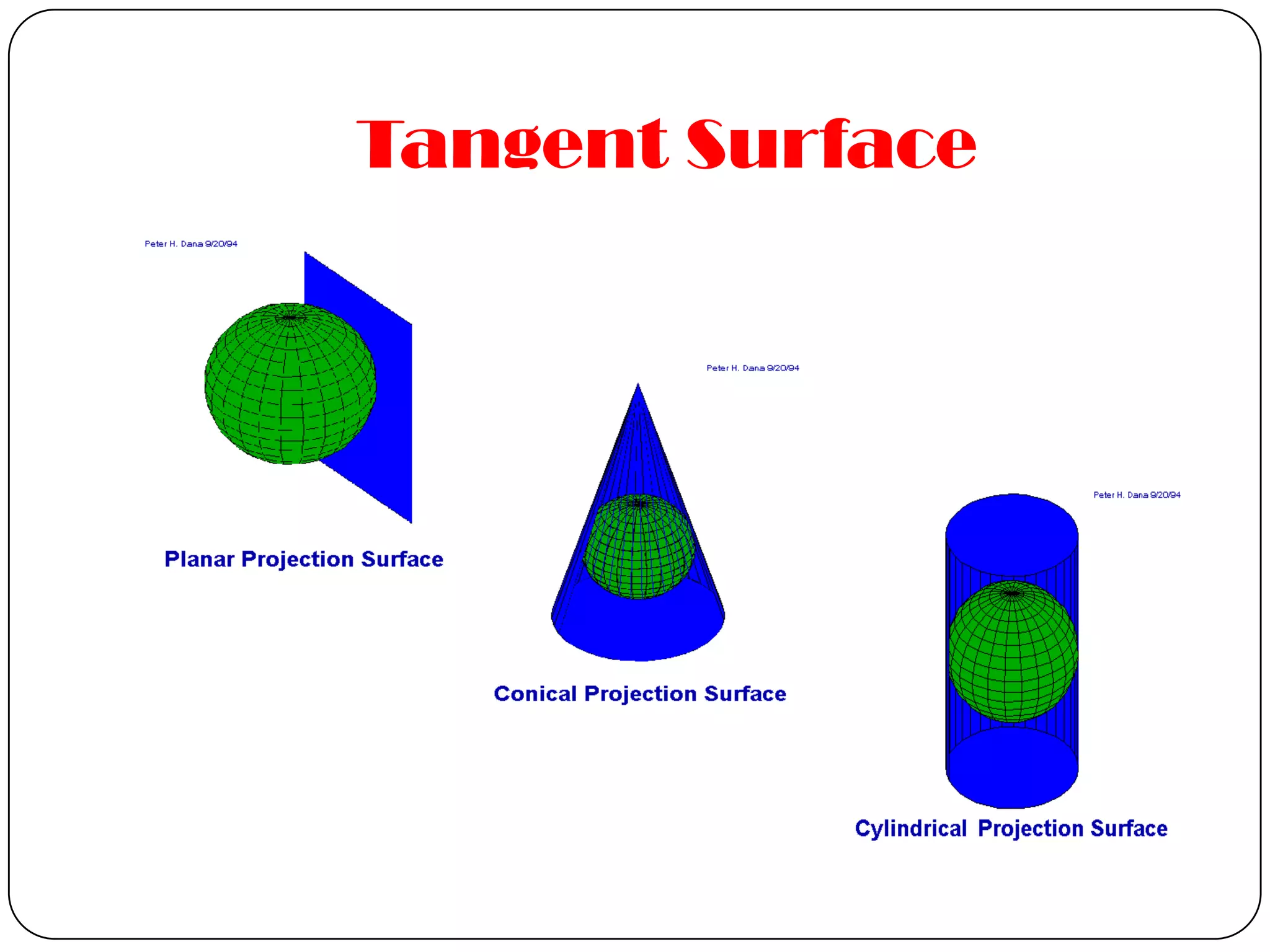
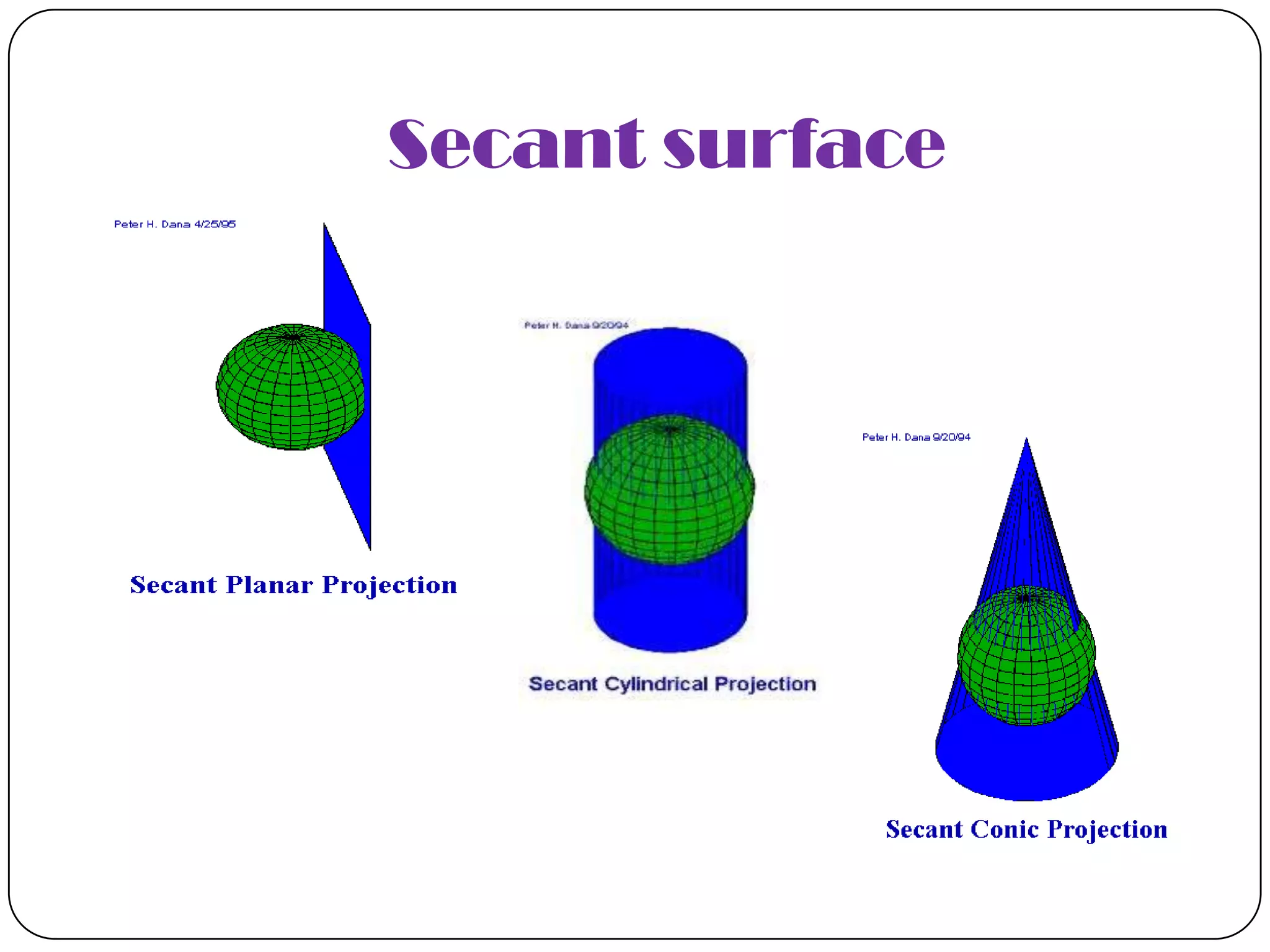
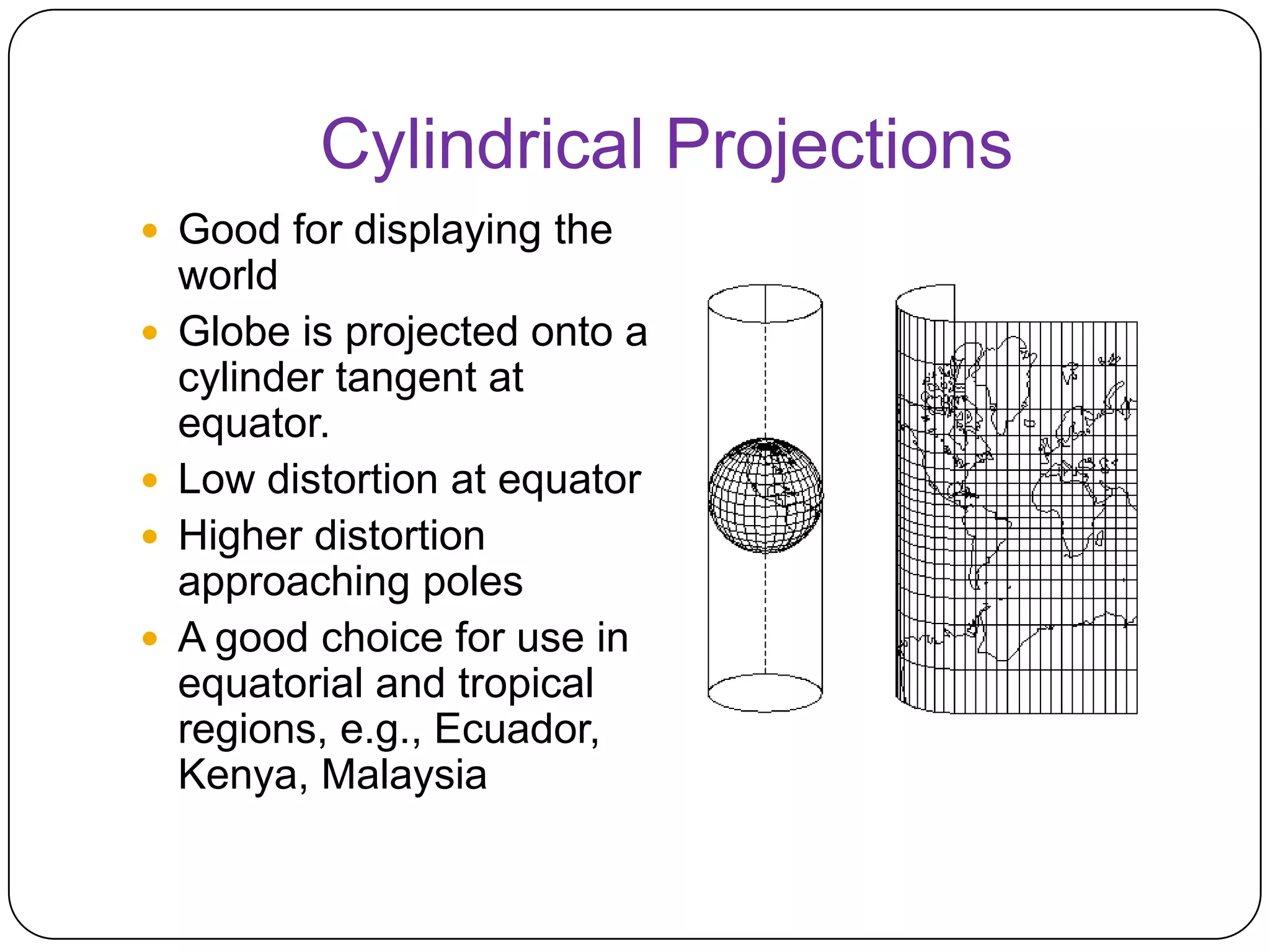
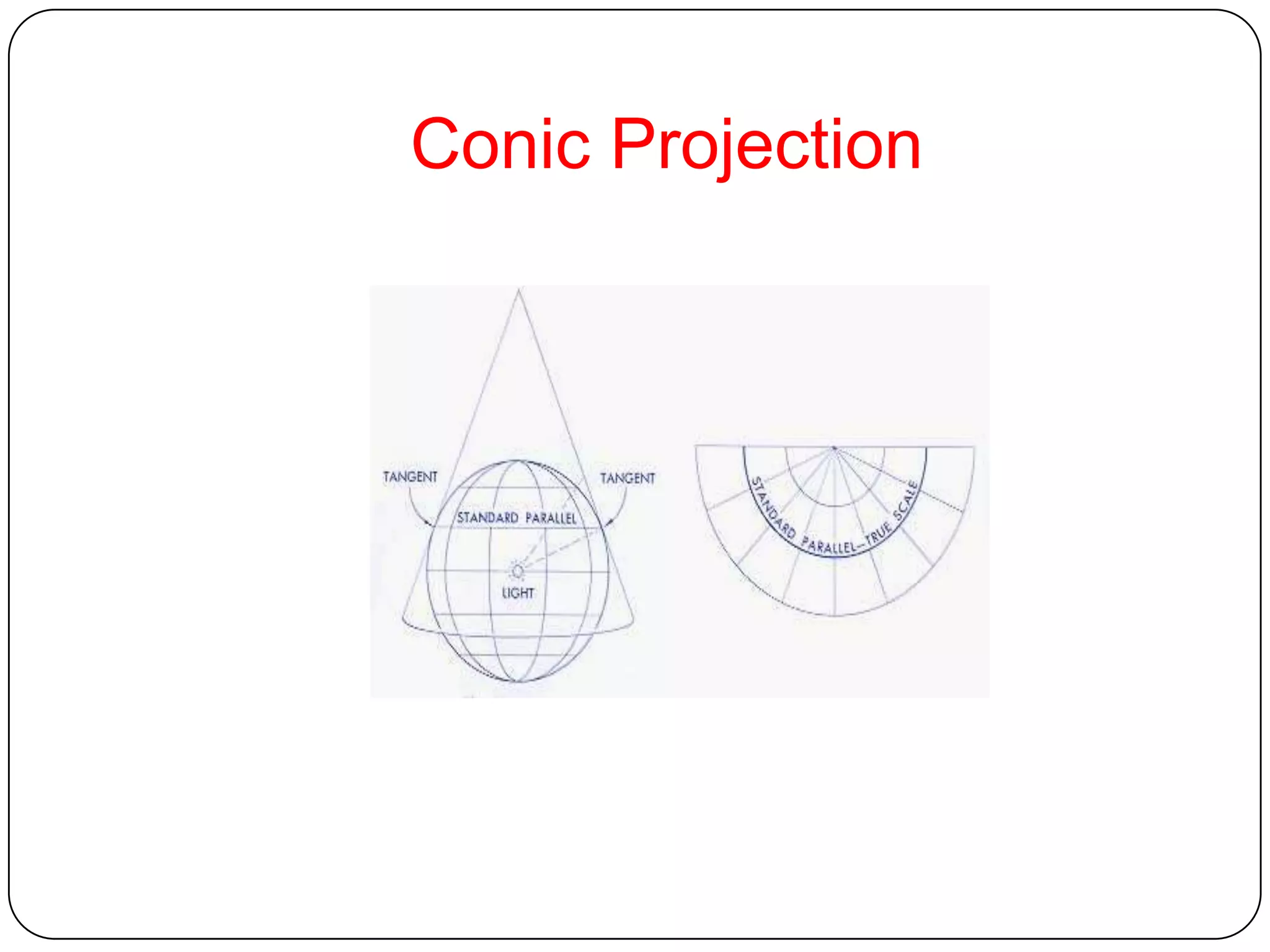
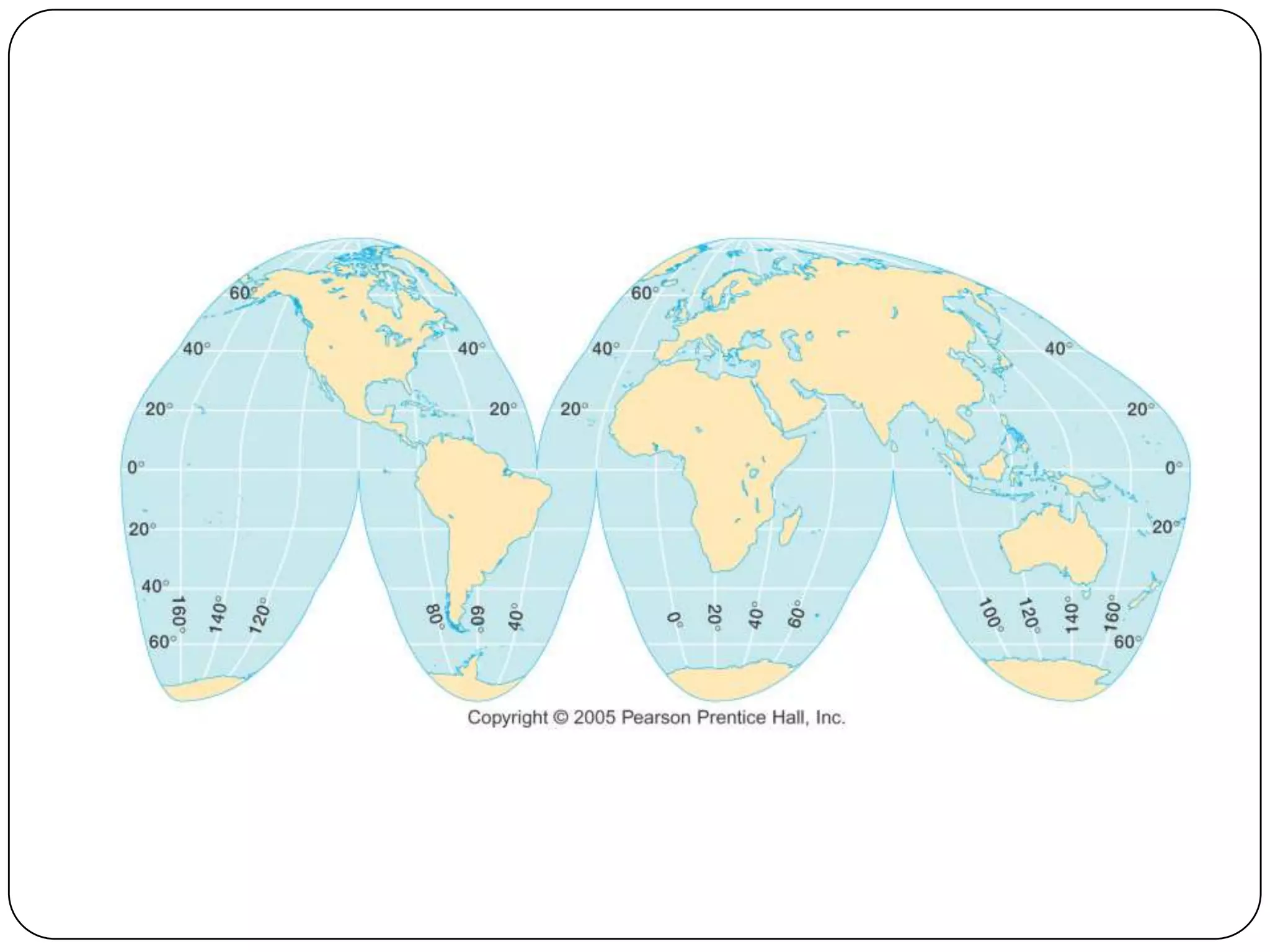
This document discusses map projections and their properties. Map projections transform the three-dimensional globe onto a two-dimensional surface, necessarily introducing some distortions. The best projection depends on the map's purpose and region. Common projections include cylindrical (like Mercator), conic, and planar/polar types. Key properties that projections aim to preserve, like shape, area, distance and direction, often involve tradeoffs. Choosing a projection minimizes distortions for a map's intended use and geographic extent.

1. An important consideration in
mapping our world
Map Projections

2. Map Projection
 Transforming
three-
dimensional space
onto a two
dimensional map.
 Define the spatial
relationship
between locations
on Earth and their
relative locations
on a map.

3. Why project data?
 Data often comes in geographic, or spherical
coordinates (latitude and longitude) and
cannot be used for area calculations.
 Some projections work better for different
parts of the globe giving more accurate
calculations.

4. “All maps lie flat, therefore all
maps lie.”

5. Issues and Limitations
Map projections are attempts to portray the surface
of the Earth or a portion of the Earth on a flat
surface.
Some distortions of different types always result
from this process.
Some projections minimize distortions in some of
these properties at the expense of maximizing errors
in others.
Some projections are attempts to only moderately
distort all of these properties.

6. Thus, the best projection depends
upon the use of the map.

7. Choosing a Map Projection
depends on
• which region to display (e.g. world, north pole,
equator, US)
• Resolution of the region
• Geometric properties of the region
• Purpose of using maps
such that distortion can be minimized

8. Distortion Types
 Conformality
When the scale of a map at any point is the same in any
direction, the projection is conformal. Meridians (lines of
longitude) and parallels (lines of latitude) intersect at
right angles. Shape is preserved locally.
 Distance
A map is equidistant when its distance from a single
location to all other locations are preserved.
 Direction
A map preserves directions when it is azimuthal, when
direction from a single location to all other locations are
preserved.

9.  Scale
It is the relationship between a distance portrayed
on a map and the same distance on the Earth.
 Area
When a map portrays areas over the entire map so
that all mapped areas have the same proportional
relationship to the areas on the Earth that they
represent, the map is an equal –area map.

10. Aspects of the Projection
 The aspect describes how the developable
surface is placed relative to the globe. It may be;
normal -such that the surface's axis of symmetry
coincides with the Earth's axis
transverse -at right angles to the Earth's axis
or oblique -any angle in between
• The developable surface may also be either;
tangent -means the surface touches but does
not slice through the globe;
secant -means the surface does slice through
the globe.

12. Tangent Surface

13. Secant surface

14. Projection Types
Projections can be conceptually created by
projecting from one geometric shape (a
sphere) onto another (a cone, cylinder, or
plane).

15. Cylindrical Projections
 Good for displaying the
world
 Globe is projected onto a
cylinder tangent at
equator.
 Low distortion at equator
 Higher distortion
approaching poles
 A good choice for use in
equatorial and tropical
regions, e.g., Ecuador,
Kenya, Malaysia

16. Example of a Cylindrical Projection:
Mercator
 Invented by Gerhardus
Mercator- Flemish
Cartographer- in 1569
 A special purpose
projection, intended as a
navigational tool
 It is conformal,
azimuthal, and has true
scale around equator.

17. Problems with Mercator
 Preserves shape (a
conformal type) but
distorts area
 Used by John Birch
Society in Cold War to
show “Red Menace”
 Africa, in reality is 14X
larger than Greenland in
area.
 Poles cannot be shown

18. Conic Projections
 Good for displaying mid- latitude area such as U.S.
 Surface of globe projected onto cone is tangent at
standard parallel.
 Distorts N & S of standard parallel(s)
 Normally shows just one semi hemisphere in middle
latitudes.

19. Conic Projection

20.  Lambert Conformal Conic is a widely used
example.

21. Planar or Polar Projection
 Good for displaying hemisphere
with one focus.
 Surface of globe is projected
onto a plane tangent at only one
point (frequently N or S pole).
 Works well in highlighting an
area.
 Shows true bearing and distance
to other points from center or
point of tangency.

22. Elliptical/Pseudocylindrical
Projection
 Also called “football” projection
 Tend to be equal- area
 Not bad for world maps
Example: Mollweide Projection

23. Goode’s Homosoline Interrupted
Elliptical Projection
 Equal-area
 Good for climate, soils, landcover – latitude and
area comparisons
 Mild distortion of shapes
 Interrupts areas- oceans, Greenland

25. Thank you for listening!
Credits to:
Chelsea P. del Rosario
Julian Philipp A. Soriano
Shaina Mavreen Villaroza