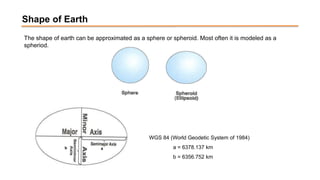
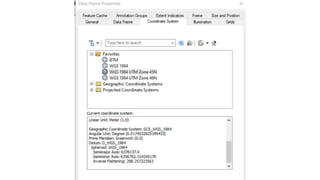
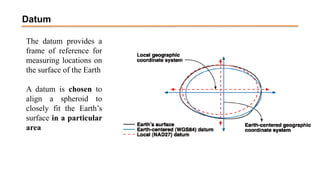
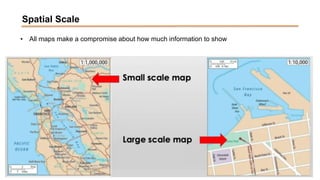
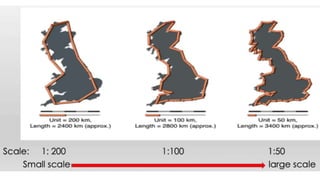
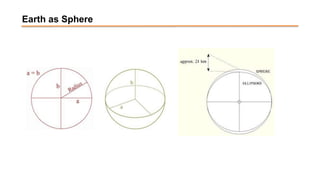
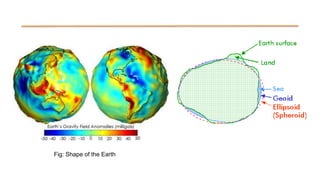
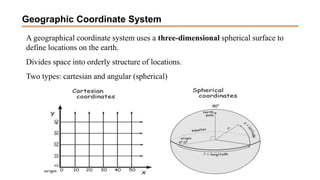
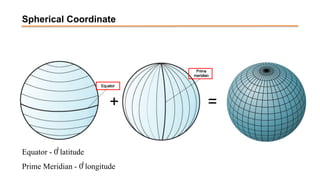
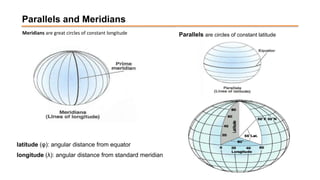
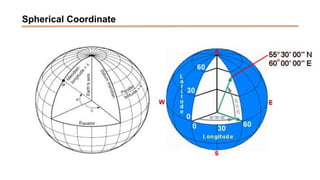
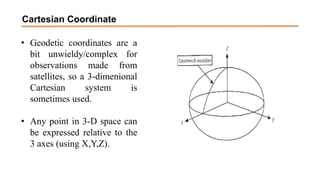
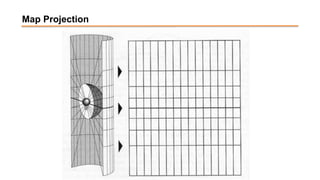
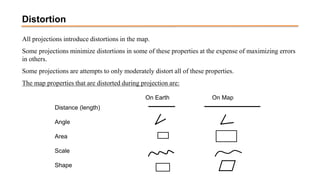
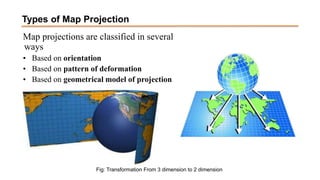
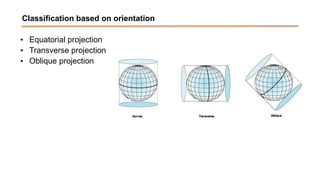
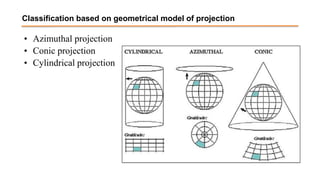
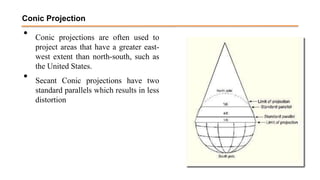
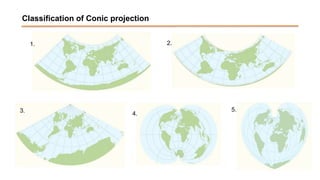
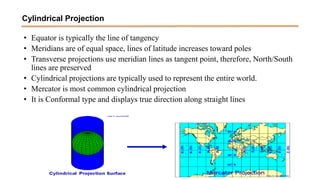
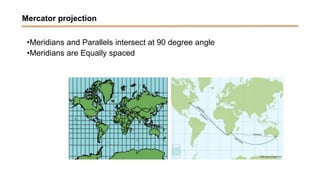
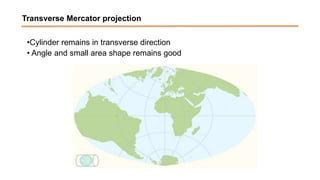
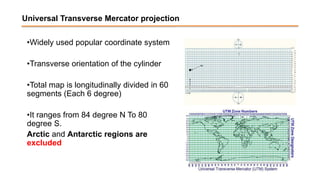
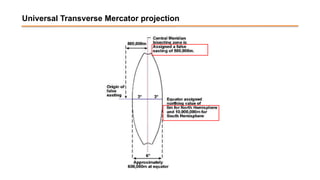
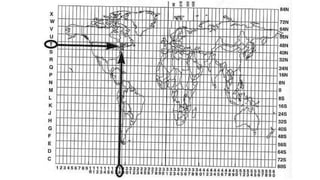
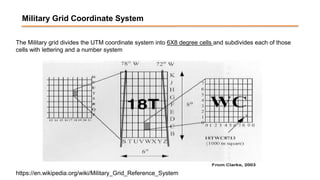
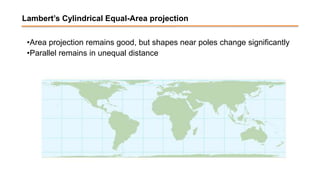
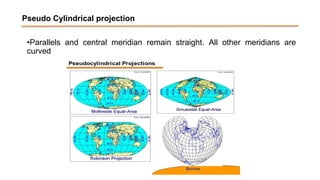
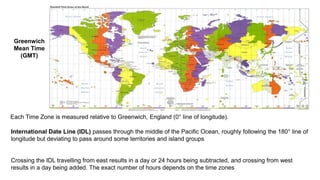
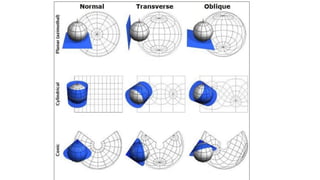
The document discusses the various spatial coordinate systems used for modeling the Earth's shape, including the use of ellipsoids and geoids for precise mapping. It covers the importance of matching datums when using geographic information systems (GIS) and describes different types of coordinate systems like geographic, projected, and Cartesian coordinates. Additionally, it explains map projections and their classifications, emphasizing that all projections introduce some degree of distortion, which can affect distance, area, and shape.

1. Spatial Coordinate System

2. Models of Earth
 When specifying location we need to use a model to
describe the shape of the Earth.
 At small scales, the Earth may be assumed to be round
(i.e. a sphere).
 At larger scales, we need to model the Earth as an
ellipsoid (an oblate spheroid).

3. The shape of earth can be approximated as a sphere or spheroid. Most often it is modeled as a
spheriod.
a
b
WGS 84 (World Geodetic System of 1984)
a = 6378.137 km
b = 6356.752 km
Shape of Earth

5. The datum provides a
frame of reference for
measuring locations on
the surface of the Earth
A datum is chosen to
align a spheroid to
closely fit the Earth’s
surface in a particular
area
Datum

6. It is important to
ensure that the datum
of a dataset matches
with the datum
setting of your GIS
and with other data
sets being used.
Datums

8. Spatial Scale
• Features on a map are obviously drawn smaller than
their actual size.
• The ratio of the drawn size to actual size is known as
scale. This can be indicated in various ways, e.g.
• 1 inch = 1 mile
• 1 inch = 63,360 inches
• 1:63,630
• The preferred method is the representative fraction
(RF).
• Large scale maps have a larger RF (i.e. they are more
‘zoomed in’ and show more detail)

9. Spatial Scale
• All maps make a compromise about how much information to show

12. Earth as Sphere

13. Fig: Shape of the Earth

14. Geoid
 An ellipsoid may not be sufficiently accurate for detailed measurements at large
scale.
 It also has ‘bumps’ and ‘hollows’.
 For geodetic measurements, the geoid is used.
 This is defined as the ‘equipotential surface that most closely corresponds to mean
sea level’.
 Mean sea level varies from place to place, so different mapping agencies use slightly
different geoids.

15. Coordinate System
Usually there are two types of coordinate system
• Geographic coordinate system
• Projected coordinate system

16. A geographical coordinate system uses a three-dimensional spherical surface to
define locations on the earth.
Divides space into orderly structure of locations.
Two types: cartesian and angular (spherical)
Geographic Coordinate System

17. Spherical Coordinate
• Once you have a model, you also need a method for expressing location (i.e. a
coordinate system)
• Treating the Earth as a sphere, the traditional approach is to use spherical
coordinates or geographical coordinates.
• These express location in terms of latitude and longitude.
• Latitude Φ is the angle at the centre of the earth between the point of interest
and the equator.
• Longitude λ is the angle at the centre of the Earth between the point of interest
and the prime meridian (i.e. the line running from pole to pole through
Greenwich).

18. Spherical Coordinate
+ =
Equator - 0̊̊ latitude
Prime Meridian - 0̊̊ longitude

19. Meridians are great circles of constant longitude
latitude (φ): angular distance from equator
longitude (λ): angular distance from standard meridian
Parallels are circles of constant latitude
Parallels and Meridians

20. Spherical Coordinate

21. Spherical Coordinate
• By convention the latitude of a place in the northern hemisphere is
positive, and in the southern hemisphere it is negative.
• Places east of Greenwich have a positive longitude, places west
have a negative longitude.
• Degrees were traditionally divided into 60 minutes, and each
minute into 60 seconds.
• For computing purposes, decimal degrees are more normally used.

22. Cartesian Coordinate
• Geodetic coordinates are a
bit unwieldy/complex for
observations made from
satellites, so a 3-dimenional
Cartesian system is
sometimes used.
• Any point in 3-D space can
be expressed relative to the
3 axes (using X,Y,Z).

23. Projected Coordinate System
• Two dimensional Cartesian coordinates are normally used for projected
maps.
• The X coordinate measures distance in an east-west direction, and the Y
coordinate measures it in a north-south direction.
• The true origin is at the centre of the map, but because negative values
are unwieldy, a false origin is usually defined to produce positive
values.
• The location of the false origin (i.e. offset) and type of projection
should be specified in the datum.

24. Measuring Distance
• Measuring distance in a Cartesian system is a simple application of
Pythagoras’s theorem:
• However, the distance estimates will vary depending upon the
projection used.
• Measuring distance using geographic coordinates is more complex
• The calculations are even more complex for geodetic coordinates.
   
y
y
x
x
d
2
1
2
1
2
2

 

 
 
2
1
2
1
2
1
1
cos
cos
cos
sin
sin
cos 




 

 
R
d

25. Map projection is the orderly transfer of positions of places on
the surface of the earth to corresponding points on a flat map.
Map Projection

26. Map Projection
• A map projection is a systematic transformation of the latitudes and
longitudes of locations on the surface of a sphere or an ellipsoid into locations
on a plane.
• Map projections are necessary for creating maps. All map projections distort
the surface in some fashion.
• Depending on the purpose of the map, some distortions are acceptable and
others are not; therefore, different map projections exist in order to preserve
some properties of the sphere-like body at the expense of other properties.
• There is no limit to the number of possible map projections.

27. Map Projection

28. All projections introduce distortions in the map.
Some projections minimize distortions in some of these properties at the expense of maximizing errors
in others.
Some projections are attempts to only moderately distort all of these properties.
The map properties that are distorted during projection are:
On Earth On Map
Distance (length)
Angle
Area
Scale
Shape
Distortion

29. Map Projection

30. Map Projection

31. Types of Map Projection
Map projections are classified in several
ways
• Based on orientation
• Based on pattern of deformation
• Based on geometrical model of projection
Fig: Transformation From 3 dimension to 2 dimension

32. Classification based on orientation
• Equatorial projection
• Transverse projection
• Oblique projection

33. • Equal area – the ratio of areas on the earth
and on the map are constant. Shape, angle,
and scale are distorted.
• Conformal – the shape of any small surface
of the map is preserved in its original form.
If meridians and parallel lines are at 90-
degree angles, then angles are also
preserved.
• Equidistant - preserve distances between
certain points. Scale is not maintained
correctly, however, typically one or more
lines has its scale maintained.
Classification based on pattern of deformation

34. Classification based on geometrical model of projection
• Azimuthal projection
• Conic projection
• Cylindrical projection

35. With Azimuthal projections, the spherical (globe) grid is projected onto a
flat plane, thus it is also called a plane projection.
Planar projections are used most often for polar regions.
Polar Equatorial
Azimuthal Projection

36. Classification of Azimuthal projection

37. Classification of Azimuthal projection
1. Gnomonic projection
2. General Perspective projection
3. Orthographic projection
4. Azimuthal conformal projection

38.  Conic Projection - tangent to the globe
along a line of latitude distortion
increases away from the standard
parallel
 The normal aspect is the north or south
pole where the axis of the cone (the
point) coincides with the pole.
 Conic projections can only represent
one hemisphere, or a portion of one
hemisphere, for the cone does not
extend far beyond the center of the
sphere.
Conic Projection

39. • Conic projections are often used to
project areas that have a greater east-
west extent than north-south, such as
the United States.
• Secant Conic projections have two
standard parallels which results in less
distortion
Conic Projection

40. Classification of Conic Projection

41. Classification of Conic projection
1. Equidistance Conic
2. Albers Equal Area Projection
3. Lambert Conformal Conic Projection
4. Polyconic Projection
5. Pseudo-Conical Projection

42. Classification of Conic projection
1. 2.
3.
4.
5.

43. • Equator is typically the line of tangency
• Meridians are of equal space, lines of latitude increases toward poles
• Transverse projections use meridian lines as tangent point, therefore, North/South
lines are preserved
• Cylindrical projections are typically used to represent the entire world.
• Mercator is most common cylindrical projection
• It is Conformal type and displays true direction along straight lines
Cylindrical Projection

44. Types of Cylindrical projection

45. Mercator projection
•Meridians and Parallels intersect at 90 degree angle
•Meridians are Equally spaced

46. Transverse Mercator projection
•Cylinder remains in transverse direction
• Angle and small area shape remains good

47. Universal Transverse Mercator projection
•Widely used popular coordinate system
•Transverse orientation of the cylinder
•Total map is longitudinally divided in 60
segments (Each 6 degree)
•It ranges from 84 degree N To 80
degree S.
Arctic and Antarctic regions are
excluded

48. Universal Transverse Mercator projection
•Each UTM zone has its own central
meridian.
•In order to avoid negative coordinate at
the west of central meridian a value is
added to central meridian, which is called
False Easting. 500,000 m False easting
value is added.
•Also to avoid negative value at the
south of Equator, a False Northing
10,000,000 m is added with the Equator

49. Universal Transverse Mercator projection
• Easting and northing are geographic Cartesian coordinates for a
point.
• Easting is the eastward-measured distance (or the x-coordinate)
and northing is the northward-measured distance (or the y-
coordinate)
• Easting and northing coordinates are commonly measured in metres
from the axes of some horizontal datum

50. Universal Transverse Mercator projection

51. Military Grid Coordinate System

53. The Military grid divides the UTM coordinate system into 6X8 degree cells and subdivides each of those
cells with lettering and a number system
Military Grid Coordinate System
https://en.wikipedia.org/wiki/Military_Grid_Reference_System

54. Military Grid Coordinate System
https://en.wikipedia.org/wiki/Military_Grid_Reference_System

55. Equidistance Cylindrical projection
•Parallel and meridian remains at right angle.
•Form equal rectangle
•Shape is retained except near pole

56. Lambert’s Cylindrical Equal-Area projection
•Area projection remains good, but shapes near poles change significantly
•Parallel remains in unequal distance

57. Pseudo Cylindrical projection
•Parallels and central meridian remain straight. All other meridians are
curved

58. Time Zones
Greenwich
Mean Time
(GMT)
Each Time Zone is measured relative to Greenwich, England (0° line of longitude).
International Date Line (IDL) passes through the middle of the Pacific Ocean, roughly following the 180° line of
longitude but deviating to pass around some territories and island groups
Crossing the IDL travelling from east results in a day or 24 hours being subtracted, and crossing from west
results in a day being added. The exact number of hours depends on the time zones

59. BTM (Bangladesh Transverse Mercator) Coordinate System
•In Flood Action Plan 19
(FAP19 study) a new
projection system was evolved
from UTM and named as BTM
Coordinate System.
•Introduced in May 1992

60. The necessary parameters of BTM projection system are listed below:
Projection: Transverse_Mercator
False_Easting: 500000.0
False_Northing: -2000000.0
Central_Meridian: 90.0
Scale_Factor: 0.9996
Latitude_Of_Origin: 0.0
Linear Unit: Meter (1.0)
Geographic Coordinate System: GCS_Everest_Bangladesh
Angular Unit: Degree (0.0174532925199433)
Prime Meridian: Greenwich (0.0)
Datum: D_Everest_Bangladesh
Spheroid: Everest_Adjustment_1937
Semimajor Axis: 6377276.345
Semiminor Axis: 6356075.41314024
Inverse Flattening: 300.8017