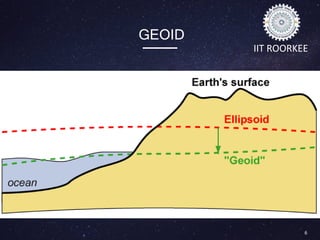
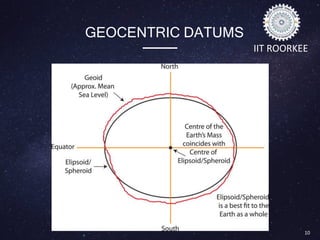
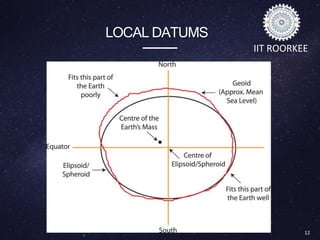
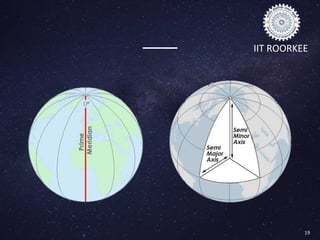
This document discusses datums in geodesy. It begins by defining a datum as a reference frame for locating points on Earth's surface. It then describes the key components of a datum including the spheroid shape it defines and parameters like semi-major axis. It discusses different types of datums such as geocentric datums based on the Earth's center and local datums that are specific to a particular region. Examples of issues with local datums are also provided. The document outlines horizontal and vertical datums, common transformation methods, and applications of datums in areas like GPS and mapping.

1. Indian Institute of Technology
Roorkee
DATUM
1
IIT ROORKEE

2. O
V
E
R
V
I
E
W
1.INTRODUCTION
2.TYPES OF DATUM
3.DATUM SHIFT
4.DATUM CONVERSION
5.APPLICATION
REFERENCES
2
IIT ROORKEE

3. INTRODUCTION
 Datum is a reference frame for locating points on Earth’s surface
 While a spheroid approximates the shape of the earth, a datum
defines the position of the spheroid relative to the center of the
earth.
 All coordinates are referenced to a datum.
 A datum describes the shape of the Earth in mathematical terms.
 A datum defines the radius, inverse flattening, semi-major axis and
semi-minor axis for an ellipsoid.
Here is the WGS84 datum:
Semi-major axis: 6,378,137.0m
Semi-minor axis: 6,356,752.3m
Inverse flattening: 294.978698214
3
IIT ROORKEE

4. “SHAPE” of the Earth
NOTE: The earth's
physical surface is a
tangible one
encompassing the
mountains, valleys,
rivers and surface of the
sea. It is highly irregular
and not suitable as a
computational surface
Earth is flattened
at the poles and
bulges at the
equator
IIT ROORKEE
4
Important terminologies

5. GEOID
 A smoothed representation of the earth is the Geoid.
 The geoid is the equipotential surface that would coincide
with the mean ocean surface of Earth.
 Using complex math and gravity readings on land,
surveyors extend this imaginary line through the
continents
5
IIT ROORKEE
Important terminologies

6. IIT ROORKEE
6
GEOID

7. SPHERE AND SPHEROID
/ELLIPSOID
 The shape and size of a geographic coordinate
system's surface is defined by a sphere or spheroid. The
assumption that the earth is a sphere is possible
for small-scale maps (smaller than 1:5,000,000). However,
to maintain accuracy for larger-scale maps (scales of
1:1,000,000 or larger), a spheroid is necessary to
represent the shape of the earth.
 A sphere is based on a circle, while a spheroid (or
ellipsoid) is based on an ellipse.
7
IIT ROORKEE

8. IIT ROORKEE
8
Ellipsoid parameters

9. TYPES OF DATUMS
1. Geocentric datums
 Based on the best earth-fitting spheroid, which relates
coordinates to the earth's center of mass.
 Uses the earth's center of mass as the origin.
 Example: WGS 1984, used for GPS
ITRF, used for estimating continental drift and
crust deformation.
9
IIT ROORKEE

10. IIT ROORKEE
10
Types of Datum
GEOCENTRIC DATUMS

11. 2. LOCAL DATUMS
 A local datum aligns its spheroid to closely fit the earth's
surface in a particular area.
 A point on the surface of the spheroid is matched to a
particular position on the surface of the earth. This point
is known as the origin point of the datum.
 The coordinates of the origin point are fixed, and all other
points are calculated from it.
 Examples: The North American Datum of 1927 and the
Australian Geodetic Datum of 1966, Everest (India-1930)
11
Types of Datum
IIT ROORKEE

12. IIT ROORKEE
12
Types of Datum
LOCAL DATUMS

13. 13

14. 2.1 INDIAN DATUM
 In the 1830s, Sir George Everest, India’s first Surveyor
General, mapped out the geodetic reference datum for
India.
 This datum, called the Everest in his honour, has since
been used as the basis for all government-issued maps of
India.
14
IIT ROORKEE
Types of Datum

15. Origin (Initial Point) Kalyanpur
Latitude of Origin 24o 07' 11''.26
Longitude of Origin 77 o 39' 17''.57
Meridional deflection of vertical -0''.29
Prime vertical deflection of
vertical
2''.89
Semi major axis of Everest
Spheroid
6,377,301 meters
Flattening of Everest Spheroid 1/300.8017
Geoidal undulation 0 meters
Azimuth to nearby control point
at Surantal
190 o 27'06''.39
Details of the Indian Datum system
15
Types of Datum

16. PROBLEMS WITH
LOCAL DATUMS
 They work in the context of relatively small portions of the Earth’ s
surface (such as the territory of India in the context of the Everest
Spheroid
 Misaligned with the Earth’s geographic centre.
 Useful for local navigation, but useless for higher military and scientific
applications that require cross-border information.
 This fact came into sharp focus during World War II when troops missed
their military targets because the geodectic datum of their country was
unconnected to that of their enemies. This was even more marked during
the Cold War when, despite the fact that both the Soviet Union and the
US were armed with intercontinental missiles, neither country could be
assured of positioning accuracy given that the maps of both countries
were drawn on reference datum unconnected with each other.
16
IIT ROORKEE

17. 17
HORIZONTAL V/S
VERTICAL DATUM
Horizontal datum is the reference value for a
system of location measurement (E.g. Lat, Long).
Vertical datum is the reference value for a system
of elevation measurement.
IIT ROORKEE

18. HORIZONTAL DATUM
 It define a zero line at the equator from which we
measure north and south (latitudes).
 There is also a zero line at the Greenwich Meridian from
which we measure east and west (longitudes).
 Together these lines provide a reference for latitude and
longitude expressed in decimal degrees. These latitudes
and longitude positions (Geographic Coordinate Systems)
are based on a spheroid or ellipsoid surfaces that
approximate the surface of the earth – a datum.
18
IIT ROORKEE
Types of Datum

19. IIT ROORKEE
19
Types of Datum

20. VERTICAL DATUM
Vertical datums are
1. Either tidal level
-based on sea levels, called tidal datum
2. Geodetic datum
-based on the same ellipsoid models of the earth used for
computing horizontal datum
20
IIT ROORKEE
Types of Datum

21. TIDAL DATUM
 Tidal datums are determined by averaging the level of water at a tide
gage over time. Some simple examples of these are Mean Sea Level
(MSL), Mean Low Water (MLW) and Mean Higher High Water
(MHHW).
 Mean Sea Level (MSL) is a tidal datum which is computed by
the Center for Operational Oceanographic Products and Services
(CO-OPS), as part of the National Tidal Datum Epoch (NTDE) based
on data collected over a 19-year tide cycle. It pertains to Local Mean
Sea Level (LMSL) at the tide station at which it was observed and
should not be confused with any other vertical datum, including
LMSL at other tide stations.
21
IIT ROORKEE
Types of Datum

22. GEODETIC DATUM
 Geodetic datums are predominantly determined through
a process of surveying known as geodetic levelling,
determining the height differences between points in the
ground known as bench marks. These height differences
can only yield actual heights at the benchmarks if at least
one datum origin point is chosen to serve as the absolute
level of the vertical datum.
22
IIT ROORKEE

23. DATUM SHIFTS
The difference in co-ordinates between datums is commonly
referred to as datum shift
23
IIT ROORKEE

24. DATUM TRANSFORMATION
 A datum transformation is a set of math formulas that
converts point coordinates from one datum to another.
24
IIT ROORKEE

25. DATUM TRANSFORMATION
Step 1: put the two sets of points into a
common coordinate space.
Step 2: align the origins of the two systems
by moving a certain number of units in
the x-direction and a certain number of
units in the y-direction.
Step 3; Then you rotate the axes into
alignment.
Step 4: you apply a scale factor.
25
IIT ROORKEE

26. DATUM TRANSFORMATION
 The process is similar in three-
dimensional space except that you
are working with a z-axis as well as
x- and y-axes. In a datum
transformation, coordinates in both
the "from" datum and the "to"
datum are converted from latitude-
longitude into three-
dimensional cartesian coordinate
space. Next, the math is done to
align the coordinates. Finally, the
coordinates are translated back into
the latitude-longitude values of the
"to" datum. 26
IIT ROORKEE

27. DATUM TRANSFORMATION
METHOD
 Three-parameter methods
 Seven-parameter methods
 NADCON (grid-based) method
 Molodensky method
27
IIT ROORKEE

28. ORIGIN OF SOME SELECTED
GEODETIC DATUMS
 https://docs.google.com/spreadsheets/d/1IzrDlMD82OobtQzVgcemh
4X33rJfWAZZU7PSkHyIsdY/edit?usp=drive_web&ouid=10573116074
6900844972
28
IIT ROORKEE

29. APPLICATION
 Geodesists and surveyors use datum to create starting or
reference points for floodplain maps, property
boundaries, construction surveys, levee design
 Datums are used in projections, monitoring the Earth’s
crust, survey boundary delineation and more.
 All coordinates are referenced to a datum – including the
one you are standing on right now.
 Used by GPS
29
IIT ROORKEE

30. REFERENCES
 https://www.colorado.edu/geography/gcraft/notes/datum/datum_f.html
 https://web.viu.ca/corrin/FRST121/recent%20stuff/Datum%20and%20Projec
tion.htm
 https://celebrating200years.noaa.gov/magazine/vertical_datums/welcome.h
tml#first
 https://www.colorado.edu/geography/gcraft/notes/datum/datum_f.html
 http://wiki.gis.com/wiki/index.php/Datum_(geodesy)
 http://www.ngi.gov.za/index.php/technical-information/geodesy-and-
gps/datum-s-and-coordinate-systems
 http://nptel.ac.in/courses/105104100/lectureB_8/B_8_10Indiandatum.htm
 http://www.geography.hunter.cuny.edu/~jochen/GTECH361/lectures/lecture
04/concepts/Datums/Datum%20transformation.htm
30
IIT ROORKEE