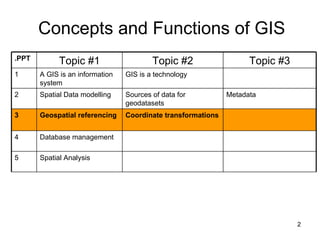
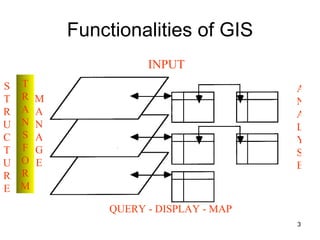
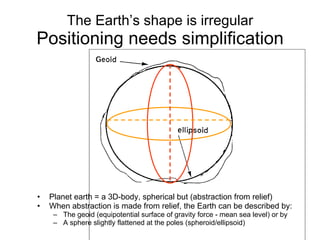
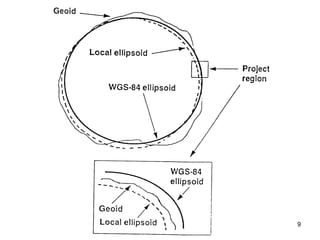
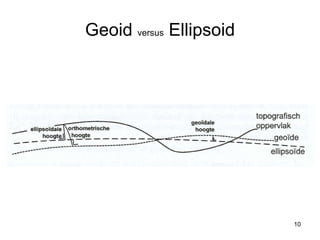
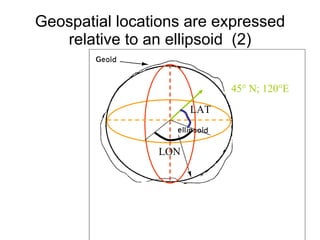
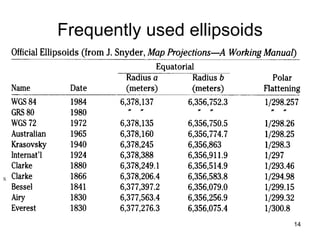
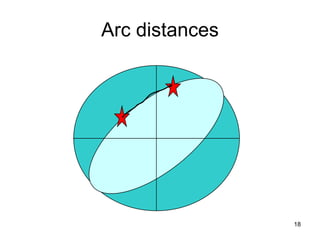
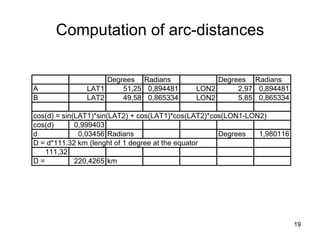
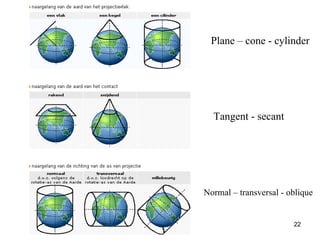
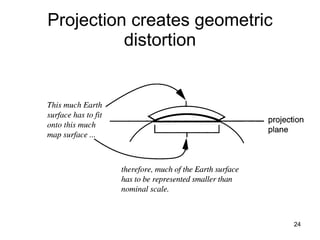
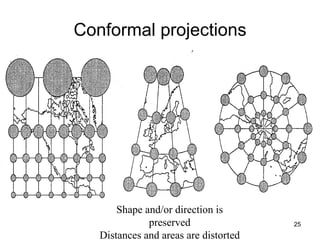
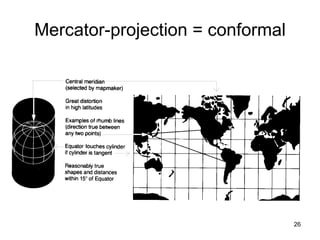
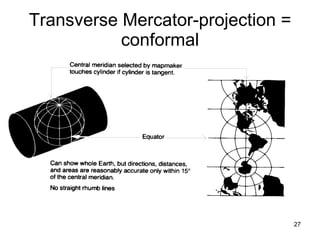
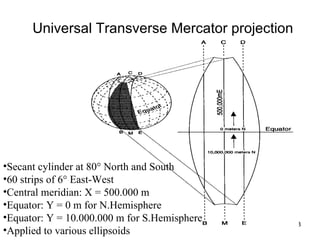
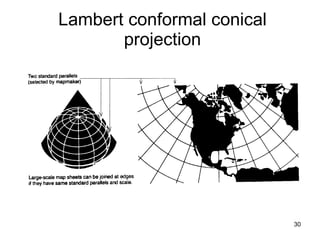
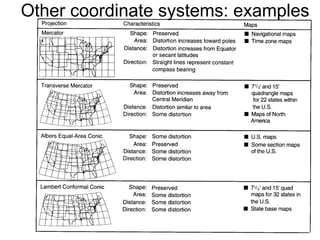
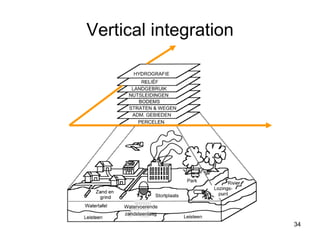
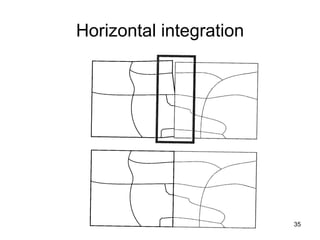
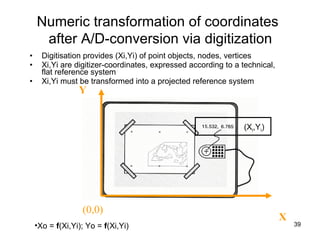
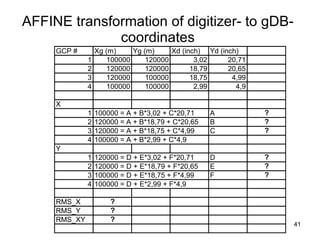
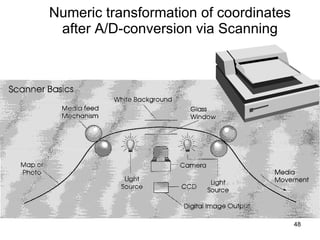
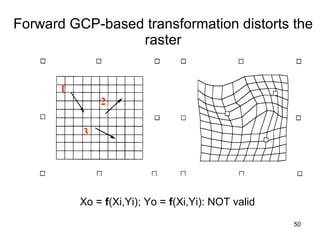
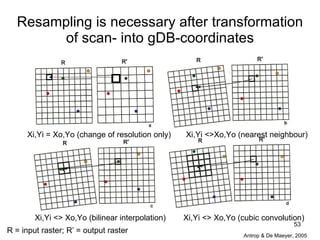
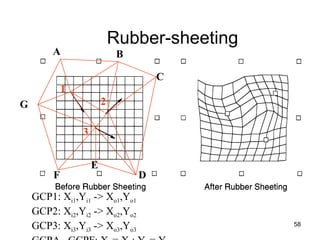
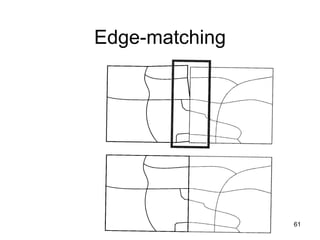
The document discusses the concepts and functions of Geographic Information Systems (GIS), focusing on spatial data modeling, geospatial referencing, and various transformations involved in GIS. It explains the roles of geodetic datums, ellipsoids, and coordinate systems in accurately representing geographical data, as well as the mathematical transformations needed to convert between different coordinate systems. The document also covers numerical coordinate transformations and techniques such as rubber sheeting and edge-matching for enhancing data accuracy in GIS applications.

1. Concepts and Functions of Geographic Information Systems (3/5) MSc GIS - Alexander Mogollon Diaz Department of Agronomy 2009

2. Concepts and Functions of GIS .PPT Topic #1 Topic #2 Topic #3 1 A GIS is an information system GIS is a technology 2 Spatial Data modelling Sources of data for geodatasets Metadata 3 Geospatial referencing Coordinate transformations 4 Database management 5 Spatial Analysis

3. Functionalities of GIS INPUT QUERY - DISPLAY - MAP ANALYSE STRUCTURE MANAGE TRANSFORM

4. Transformations for building a spatial model / gDB Of the geometric data (coordinates, cell definition) Of the attribute data change of units combination of attributes: e.g. time = distance/speed ...

5. Transformation of coordinates and Geospatial refence systems Spatial reference system is required to define geometric location and shape; uses ‘coordinates’ Geospatial reference system (‘ coordinate reference system – CRS ’) is required for modelling entities and terrain occurring on/below/above the surface of the Earth A/D-conversion, remote sensing, ... provide data about location and shape in a technical spatial reference system Transformation of coordinates towards a geospatial reference system is imperative Two classes of geospatial reference systems Geographic Projected Very many variants exist of both Transformations required for vertical integration

6. Planet Earth

7. The Earth’s shape is irregular Positioning needs simplification Planet earth = a 3D-body, spherical but (abstraction from relief) When abstraction is made from relief, the Earth can be described by: The geoid (equipotential surface of gravity force - mean sea level) or by A sphere slightly flattened at the poles (spheroid/ellipsoid)

8. Geoid versus Ellipsoid Geoid 3D-physical datamodel of the Earth’s surface, based on measurements of the gravity force Local and Global Ellipsoids Mathematical 3D-models of the Earth’s surface Global ellipsoids are defined to represent the full Earth with acceptable accuracy Local ellipsoids are defined to represent a part of the Earth’s surface only, with high accuracy

10. Geoid versus Ellipsoid

11. Geospatial locations are expressed relative to an ellipsoid (1) Geographic coordinates: Expressed as angles with respect to 2 of 3 axes through the gravity point of the ellipsoid LONGITUDE: 0° (Greenwich) to 180° East and 0° to 180° West measured in the horizontal plane LATITUDE: 0° (Equator) to 90 North and 0° to 90° South) measured in the vertical plane Degrees-Minutes-Seconds or Decimal Degrees: 20° 15’ 15” = 20,2525

12. Geospatial locations are expressed relative to an ellipsoid (2) LON LAT 45° N; 120°E

13. Geospatial locations are expressed relative to an ellipsoid (3) Several ellipsoids are in use ! Major radius or major semi-axis a Minor radius or minor semi-axis b Flattening f of the ellipsoid: a-b/a = 1/f

14. Frequently used ellipsoids S

15. Geospatial locations are expressed relative to an ellipsoid (4) Geodetic datum = further specification of the ellipsoid Initial location Initial azimuth to define the north direction Distance between geoid and ellipsoid at the initial location Basis for conversion between LON-LAT and geocentric coordinates (x,y,z) A given point has different LON-LAT when expressed against different ellipsoids ! A given point has different geocentric coordinates x,y,z when expressed against different datums, even if the ellipsoid is identical

16. From geographic coordinates to projected coordinates Common GIS-systems model the geographic reality in planimetric 2D traditional map view Carthesian X-Y coordinates, meters LON-LAT (angles, 3D) need to be transformed into X-Y (2D) Such a transformation = a projection Projected coordinates = map coordinates

17. From geographic coordinates to projected coordinates gDB may store Geographic coordinates or Projected coordinates Distances, lengths and areas cannot be expressed in geographic coordinates = Essential for most queries and spatial analyses If geographic coordinates are stored, most often run time or “on the fly” transformation into projected coordinates is done by the GIS-software when querying, analysing the gDB

18. Arc distances

19. Computation of arc-distances

20. From geographic coordinates to projected coordinates From LON-LAT to X-Y = mathematical, analytical operation 1. Shape of earth needs to be parameterised by means of a geodetic datum global or local approximation of the geoid

21. From geographic coordinates to projected coordinates From LON-LAT to X-Y = mathematical, analytical operation 2. One of very many projection functions needs to be choosen Cylinder, plane or cone as projection surface Tangent or secant at selected locations Normal, transversal, arbitrary False easting, false northing

22. Plane – cone - cylinder Tangent - secant Normal – transversal - oblique

23. Choice of the projection function From 3D to 2D => deformation cannot be avoided shape direction area distance Local datum and projection function are choosen in order to minimise deformation for the study area position and shape of study area conditioned by objective of cartography (density mapping requires ‘true’ areas) and type of analysis

24. Projection creates geometric distortion

25. Conformal projections Shape and/or direction is preserved Distances and areas are distorted

26. Mercator-projection = conformal

27. Transverse Mercator-projection = conformal

28. Universal Transverse Mercator projection Secant cylinder at 80° North and South 60 strips of 6° East-West Central meridian: X = 500.000 m Equator: Y = 0 m for N.Hemisphere Equator: Y = 10.000.000 m for S.Hemisphere Applied to various ellipsoids

29. Standard projected coordinate system for the Philippines Ellipsoid: Clark’s spheroid of 1866 Semi-major axis = 6.378.206,4 m Semi-minor axis = 6.356.583,8 m Projection: Philippines Transverse Mercator UTM Zone 50 (114 – 120 °East) Zone 51 (120 – 126 °East) Further subdivided in 6 subzones with central meridian 117 °East 119 °East 121 °East 123 °East 125 °East False northing = 0; False easting = 500.000 meters

30. Lambert conformal conical projection

31. Standard projected coordinate system for Belgium Belgian Datum = local orientation of Hayford’s ellipsoid of 1909, recommended as International ellipsoid in 1924 Projection function : Lambert 72/50 Conformal conical projection with 2 secant parallels 49°50’0.0204” and 51°10’0.0204” Longitude of central meridian: 4°22’2.952” Latitude of origin: 90° Fase easting: 150.000,013 meter False northing: 5.400.088,4398 meter Vertical reference system = TAW (average low tide level in Oostende (North Sea Channel )

32. Other coordinate systems: examples

33. A gDB Can have one coordinate reference system only (effective or virtual) The coordinates in all geodatasets must be expressed according to that system Vertical integration Horizontal integration Most commonly, the choosen coordinate system is Geographic coordinates (LON-LAT) or National coordinate system (from the National Mapping Agency, used for printing topographic / military maps)

34. Vertical integration

35. Horizontal integration

36. Transformation of coordinates for vertical/horizontal integration Analytical conversion between geographic coordinates expressed according to different geodetic datums = datum conversion Analytical conversion of geographic coordinates (e.g. from GPS) in projected coordinates and vice versa = (inverse) projection Analytical conversion between different types of projected coordinates (e.g. between Philippine and Belgian system) Numerical coordinate transformation (e.g. geo-referencing, using control points)

37. Numeric coordinate transformation Numeric coordinate shifts, based on control points, for vertical and horizontal integration of geodatasets in a gDB systematic shifts (e.g. conversion of digitiser/scan coordinates in projected coordinates) non-systematic shifts: rubber sheeting, edge matching

38. Geo-referencing When coordinates are expressed according to an analytical reference system, the term ‘georeferenced data’ is used. A/D conversion using tablet digitising or scanning provide digitiser and scan coordinates. Also raw satellite images are not georeferenced. Transformation of « technical » coordinates into geographical or projected coordinates = georeferencing .

39. Numeric transformation of coordinates after A/D-conversion via digitization Digitisation provides (Xi,Yi) of point objects, nodes, vertices Xi,Yi are digitizer-coordinates, expressed according to a technical, flat reference system Xi,Yi must be transformed into a projected reference system X Y (0,0) Xo = f (Xi,Yi); Yo = f (Xi,Yi) (X i ,Y i )

40. Numeric transformation of digitizer- to gDB-coordinates AFFINE polynomial transformation function f = popular Xo = A + BXi + CYi Yo = D + EXi + FYi 2 * 3 unknowns: A, B, C and D, E, F 2 * 3 equations required to compute the unknonws Equations are derived from 3 control points (3X and 3Y) (GCP) GCP = ground control point = point location that can be unambiguously detected and located on both the dataset which must be transformed and on the reference geodataset or reality System of equations has one single EXACT solution for A ... F Transformation error is apparently 0 If more than 3 GCP are available, more equations than unknowns System of equations has more than one solution for A ... F Best solution for A ... F can be found by the Least-Squares method Transformation error can be computed (RMSe - ROOT MEAN SQUARE ERROR) If RMSe is sufficiently low Parameterised AFFINE equations can be applied to all input-points (point objects, nodes, vertices). Result = transformed output-geodataset

41. AFFINE transformation of digitizer- to gDB-coordinates

42. AFFINE-transformation & RMSe: X

43. AFFINE-transformation & RMSe: Y

44. AFFINE-transformation & RMSe: X & Y

45. Judgement of the RMSe To be based on the spatial detail (scale for A/D-converted analog documents) of the source document 1 mm distortion and/or digitizing error on a 1:50.000 analog map = 50 meter RMSe To be based on the intended use of the output-geodataset Requirements for vertical and horizontal integration

46. Translation: X o = A + X i Y o = D + Y i Change of scale: X o = BX i Y o = EY i Rotation: X o = BX i + CY i Y o = EX i +FY i AFFINE = All combined X o = A + BX i + CY i Y o = D + EX i + FY i AFFINE = polynomial transformation of the 1st order

47. X o = a 0 +(a 1 X i +a 2 Y i )+(a 3 X i 2 +a 4 .X i Y i +a 5 Y i 2 )+… Y o = b 0 +(b 1 X i +b 2 Y i )+(b 3 X i 2 +b 4 .X i Y i +b 5 Y i 2 )+… Order of the polynomial p determines the minimum number of required GCP to find the polynomial coefficients: N = (p+1)*(p+2)/2 Polynomial transformations of higher orders (rubber sheeting, warping)

48. Numeric transformation of coordinates after A/D-conversion via Scanning

49. Numeric transformation of scan- to gDB-coordinates A scanned document is not georeferenced Scan-coordinates are relative to the reference system of the scan-device Transformation of the scan-coordinates is necessary, using GCP Regular cell-raster is distorted A new ‘empty’ cell-raster is created according to the output-reference system Based on the established transformation function, cell values are resampled from the input raster to compute the values for the cells in the output raster Neirest neighbour Other algorithms Also valid for remotely sensed images !

50. Forward GCP-based transformation distorts the raster 1 2 3 Xo = f (Xi,Yi); Yo = f (Xi,Yi): NOT valid

51. Backward/Inverse polynomial transformation of scan- to gDB-coordinates Creation of a new ‘empty’ rasterstructure in the output-coordinate system Calibration of the inverse polynomial transformation Xi = f(Xo,Yo) Yi = f(Xo,Yo Use of the calibrated transformation function to ‘fill’ the empty cells of the output raster with (a combination of) the value(s) of the corresponding cell(s) in the input raster

52. Resampling GCP are used to calibrate an inverse polynomial transformation function, e.g. AFFINE X i = G + HX o + IY o Y i = K + LX o + MY o By means of this function, for the mid point of every output-cell (Xo,Yo) the corresponding point (Xi,Yi) in the input raster is computed Xi,Yi is the ‘nearest neighbour’ With ‘nearest neighbour resampling’, the cell value of the cell in which Xi,Yi is located is attributed to the output cell with midpoint Xo,Yo Also bi-linear and curbic re-sampling are possible

53. Resampling is necessary after transformation of scan- into gDB-coordinates R = input raster; R’ = output raster Antrop & De Maeyer, 2005 Xi,Yi = Xo,Yo (change of resolution only) Xi,Yi <>Xo,Yo (nearest neighbour) Xi,Yi <> Xo,Yo (bilinear interpolation) Xi,Yi <> Xo,Yo (cubic convolution)

54. Numeric coordinate transformation Similar systematic numeric transformation is applicable to coordinates coming from other data sources Remotely sensed images Theodolites, tachymeters with digital reading Global Positioning Systems (GPS)

55. (Non-)systematic numeric coordinate-transformations Previous numeric polynomial coordinate transformations are based on GCP One set of coefficients A, B, C, … is computed and applied to all input-points to obtain the output-coordinates Such transformations are systematic

56. Non-systematic transformations for further improvement of the positional quality of the georeferenced geodatasets First step in georeferencing is most often a systematic transformation of coordinates Polynomial function of low order The result is often not of sufficient quality or not sufficiently fit for use (vertical/horizontal integration in the gDB) In a next step, non-systematic transformation can be performed to make the geodataset geometrically more conformal to the reference geodataset

57. Non-systematic coordinate transformations Edge-matching Rubber-sheeting

58. Rubber-sheeting 1 2 3 GCP1: X i1 ,Y i1 -> X o1 ,Y o1 GCP2: X i2 ,Y i2 -> X o2 ,Y o2 GCP3: X i3 ,Y i3 -> X o3 ,Y o3 GCPA...GCPF: X i = X o ; Y i = Y o A B D E F G C

59. Rubber-sheeting Point-by-point correction of the location and shape of objects or of resampling of cell attributes Based on 2 linear “piece wise” TIN-interpolations (7.PPT), 1 for X and 1 for Y Z-value to interpolate = X o resp. Y o Result = not-constant translation/rotation/change of scale Shifts decrease with increasing distance Both forward (for vectorial geodatasets) and backward (for raster datasets)

60. Edge-matching Special case of rubber sheeting Applied for horizontal integration of adjacent (A/D converted) map sheets or images (mosaicking) Definition of links between coinciding points on two map sheets Differential displacement of points based on (mostly inverse distance; TIN) interpolation

61. Edge-matching

62. Summary of important items Geospatial reference systems Based on a geodetic datum (LON-LAT) and (possibly) a projection function to convert LON-LAT (angles - 3D) into planimetric coordinates (X,Y – 2D) Projection leads to distortion of one or more of shape, direction, area, distance If the national standards are not used, a rational, functional choice of datum and projection function is required The datum for elevation is most often the geoid (approximated by mean sea level) Transformation of coordinates Between parameterised geographic and/or projected coordinate systems is an analytical operation which does not need external ground truth Between technical coordinates and projected coordinates is a numeric operation based on ground truth (GCP) There are systematic and non-systematic numeric transformation functions Systematic transformation is most often based on a polynomial function Non-systematic transformation (rubber sheeting and edge-matching) is based on TIN-interpolation The latter is also valid for projected coordinates which need correction

63. Questions or remarks ? Thank you …