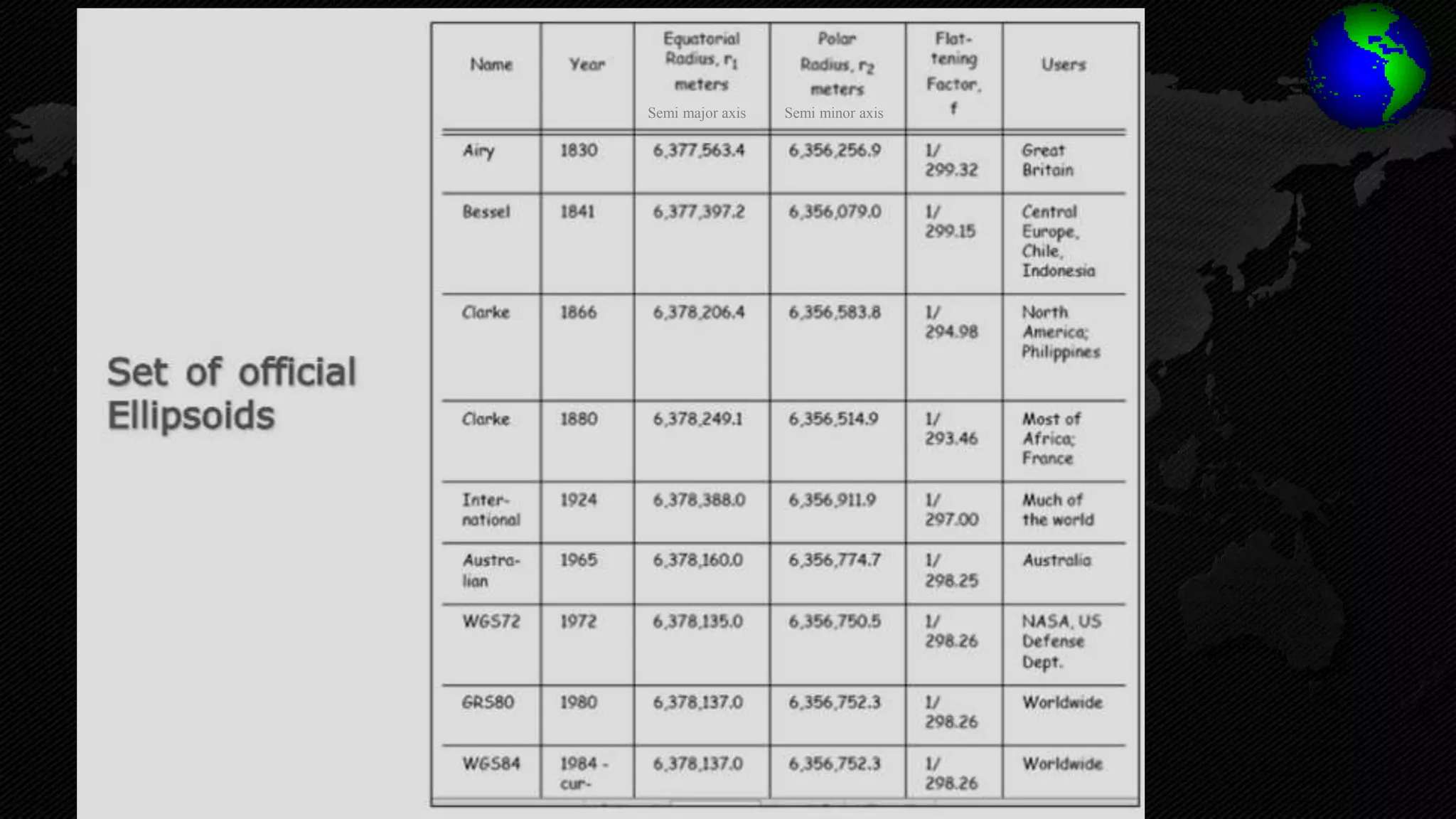
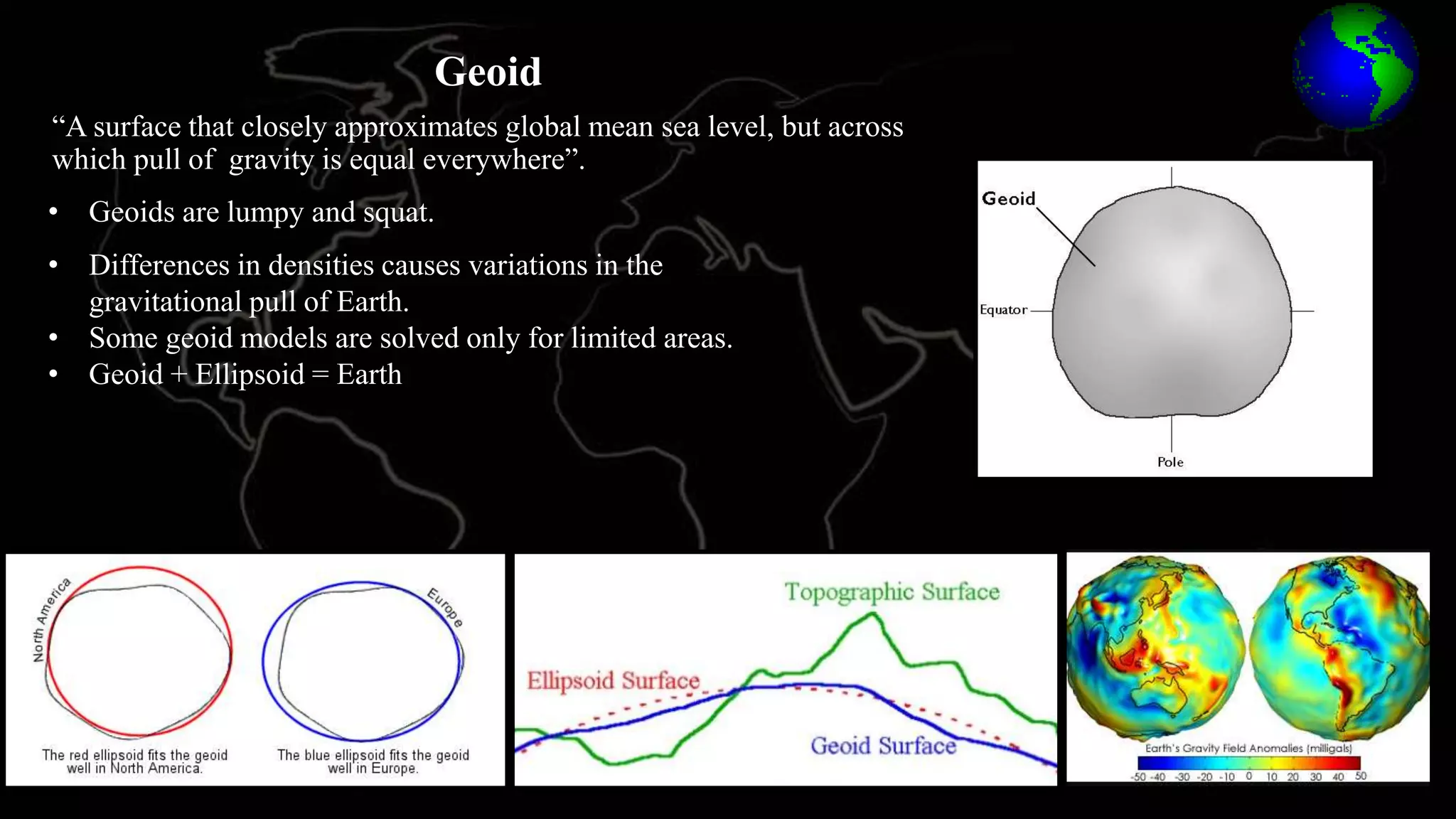
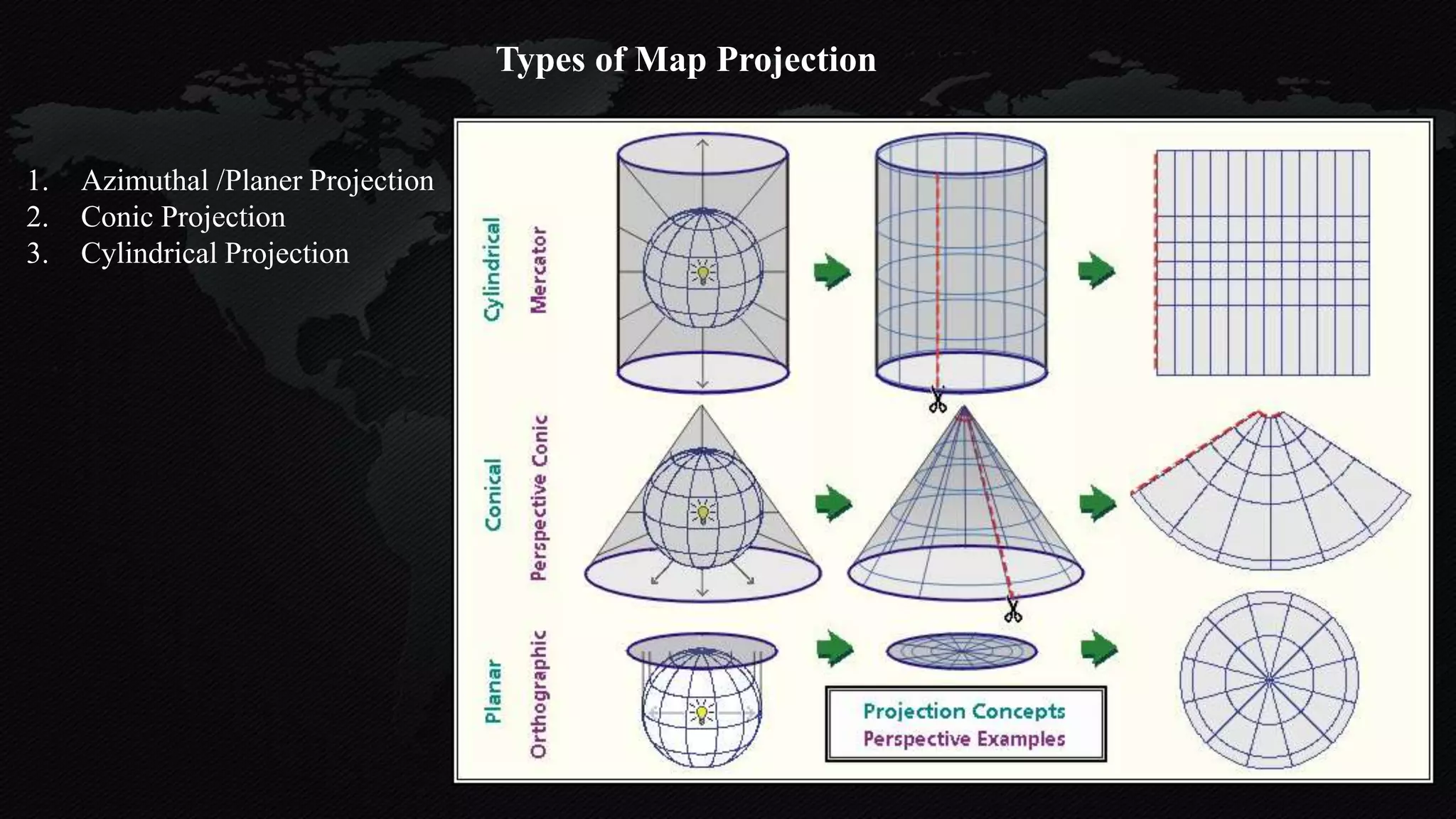
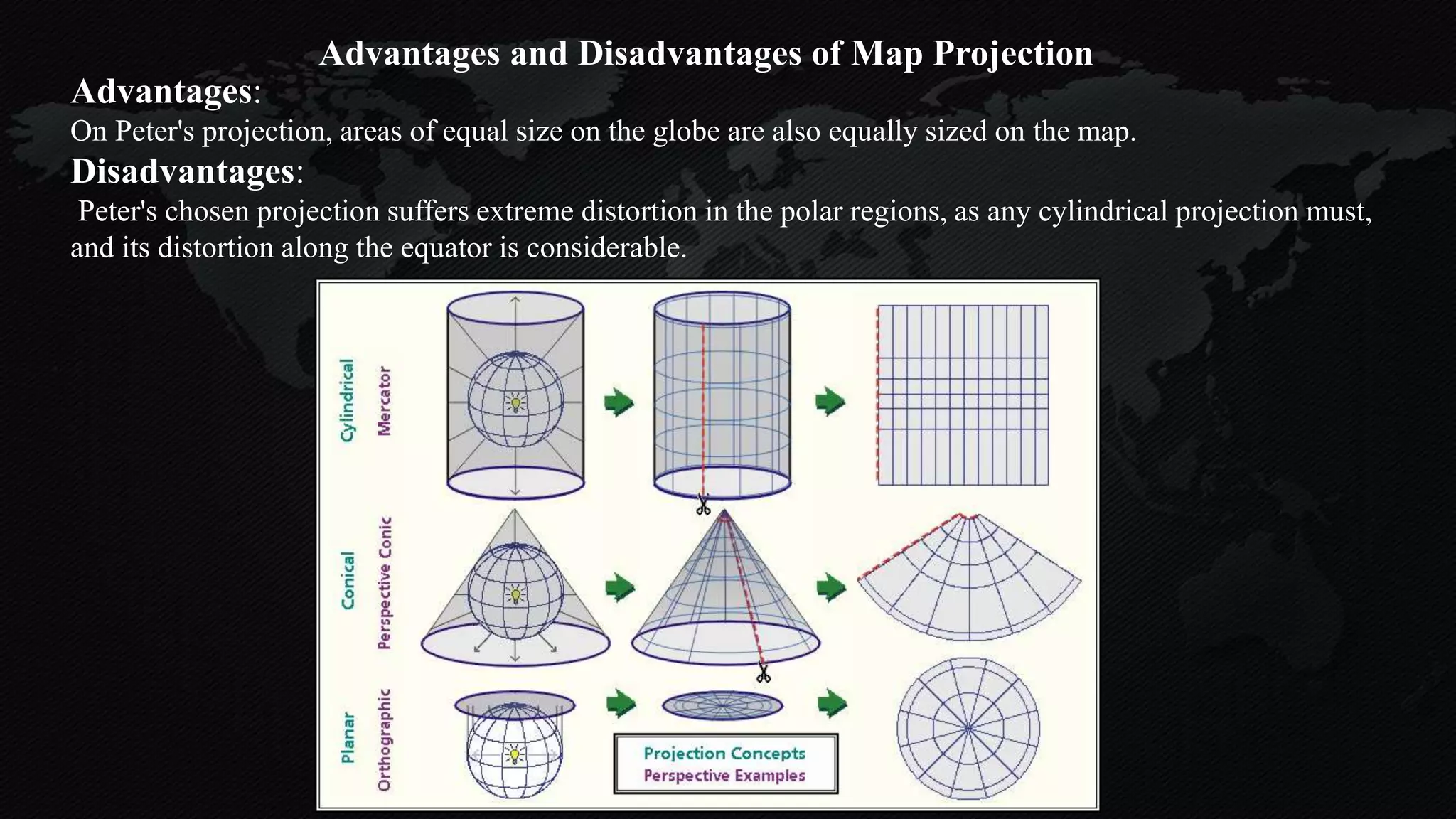
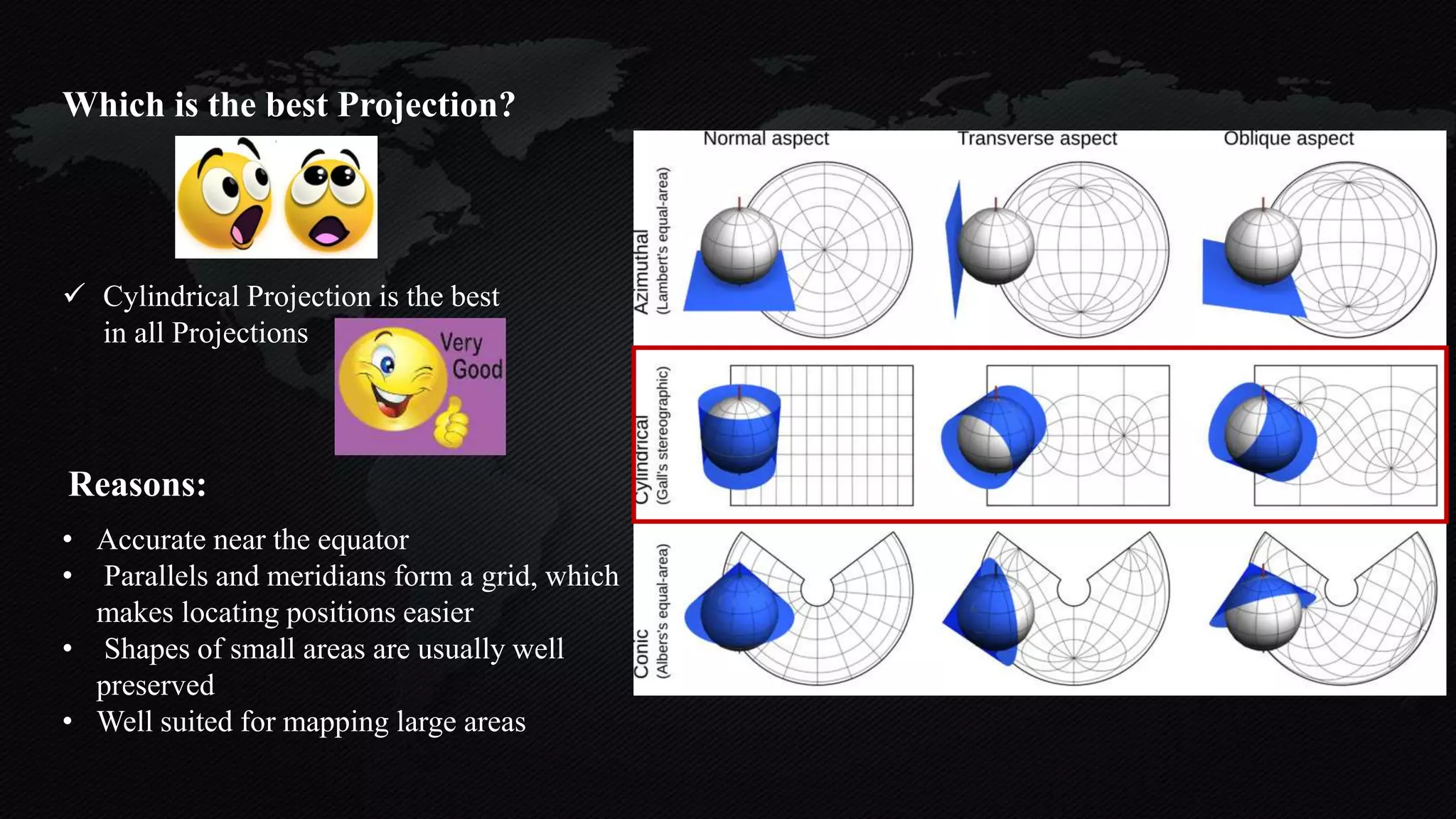
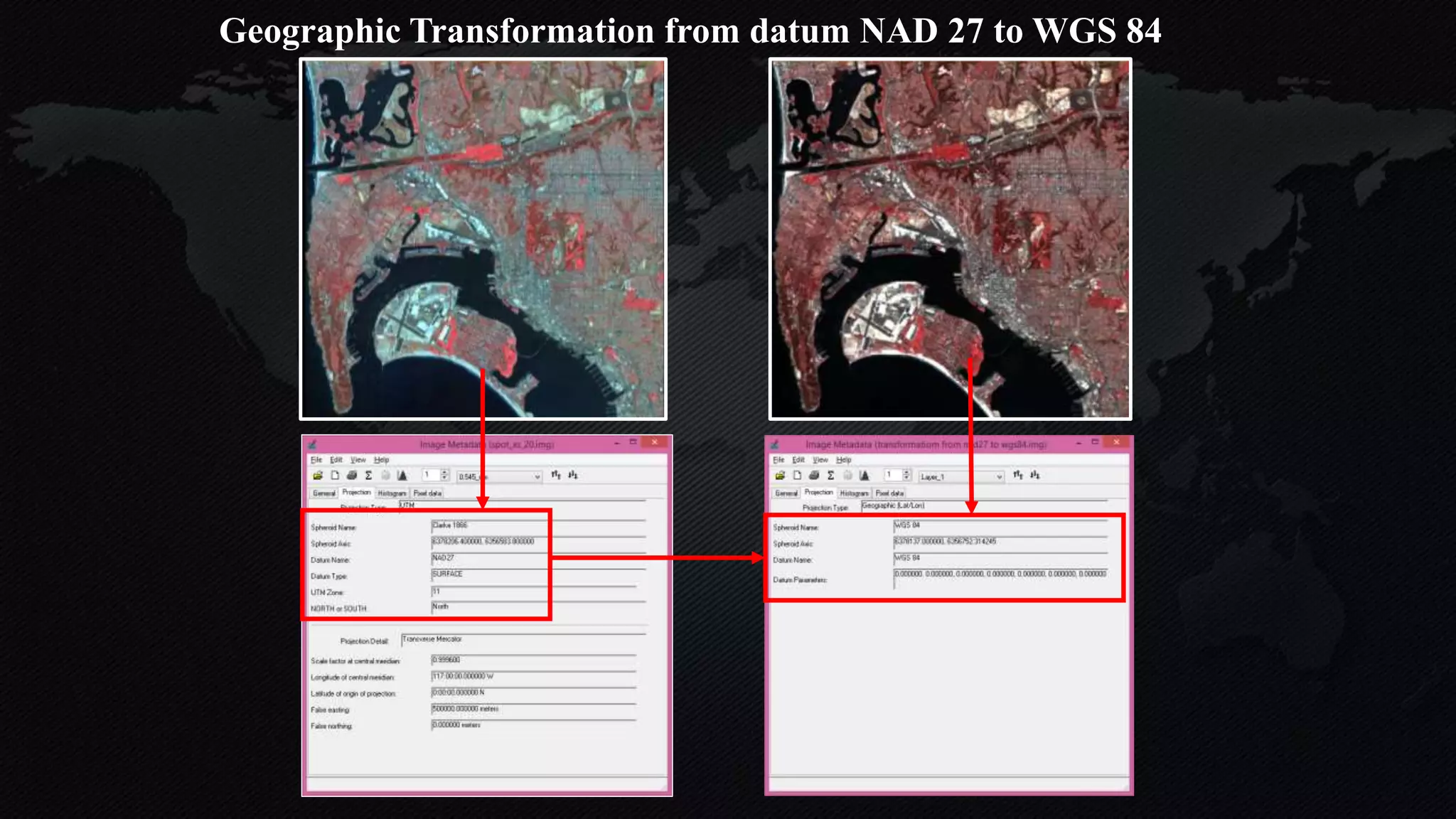
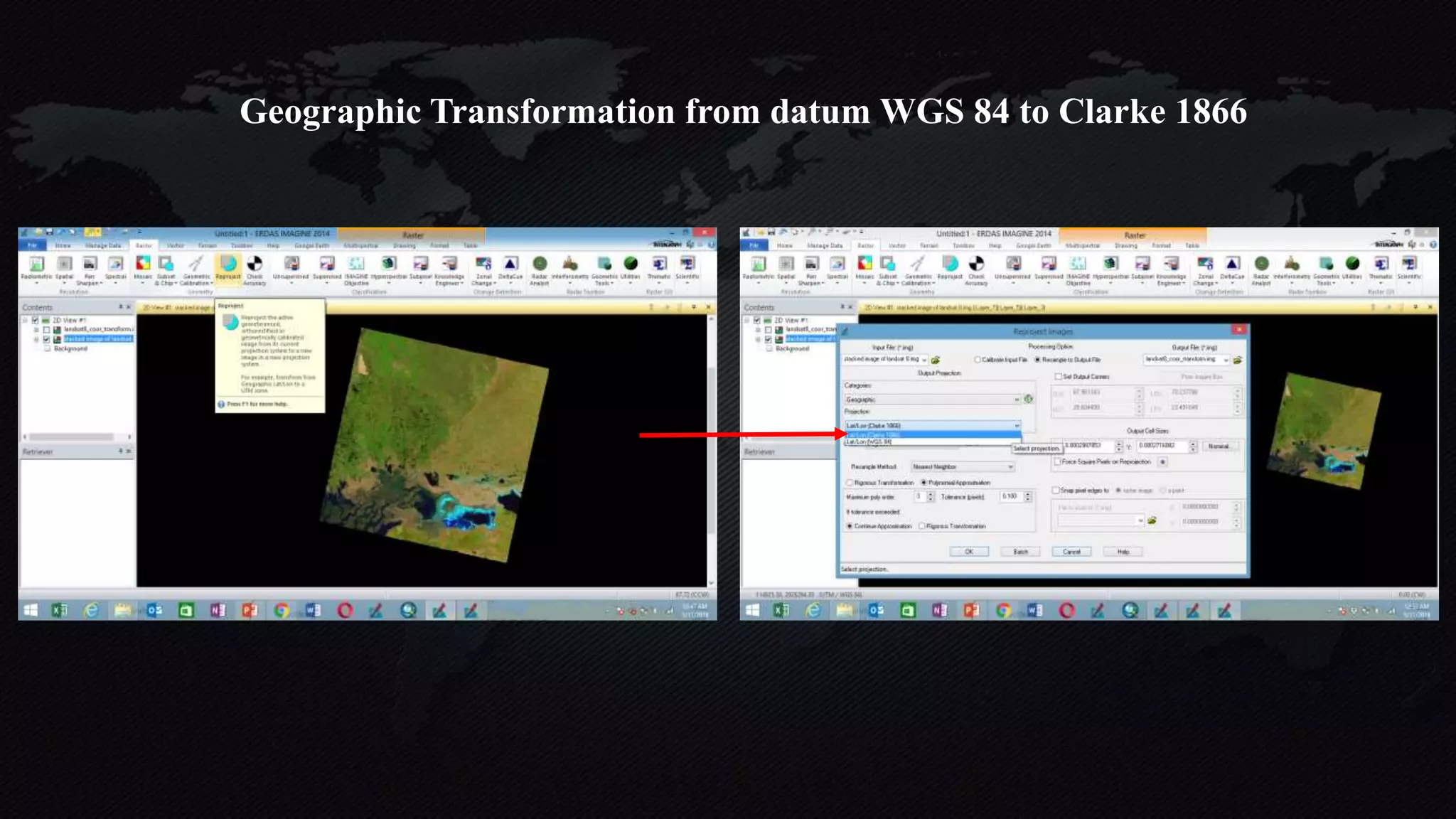
The document discusses earth coordinate systems, focusing on concepts such as datum, spheroid, and various map projection types. It explains the importance of geodesy, the shape of the earth, and different coordinate systems, including geographic and projected systems. Additionally, it compares map projections, highlighting their advantages and disadvantages, particularly the cylindrical projection as the most suitable for large areas.

1. “EARTH COORDINATE
SYSTEMS”
Presented by:
Sheikh Maryam (SS15-10)
Sumar Farooq (SS15-09)
Ammara Khalid (SS15-14)
Datum, Spheroid, Horizontal and Vertical Datums, Projection Systems,
Properties, Types, Coordinate Transformation, Uses.
UTM Projection System.
Datum and Projection Systems for Pakistan.
Compare your work with Google Earth.

2. Contents
• Geodesy
• Shape of earth
• Conceptual models (Ellipsoid/Spheroid, Geoid)
• Datum and their types
• Earth Coordinate Systems
• Map Projection and their types
• Which is the best Projection
• Coordinate transformation

3. Geodesy
Science of measuring the three categories
• Shape of Earth and
• Its gravity field
Why Geodesy is important?
• The earth has an irregular shape that is difficult to model.
• The earth has gravity anomalies from one place to another.

4. Shape of Earth

5. Conceptual Models of Earth

6. Reference Ellipsoid?
• A reference ellipsoid is a
mathematically-defined surface that
approximates the geoid, the truer
figure of the Earth, or other planetary
body.
Ellipsoids approximates geoid
Ellipsoid/Spheroid
• “An ellipsoid is a three-dimensional geometric figure that resembles a sphere,
but whose equatorial axis (a) is slightly longer than its polar axis (b)”.
Sphere and ellipsoid
Best Fitted Ellipsoid
• Sphere is based on a circle where a spheroid (ellipsoid) is based on an ellipse.
• Semimajor axis (a)
• Semi minor axis (b)
• Flattening (f) f = a-b/a
• Flattening ranges from 0 to 1.
• Flattening of Earth 0.003353
• Global Ellipsoid (GRS 1980, WGS 84)
• Local and regional ellipsoid
(Clarke 1880)

7. Semi major axis Semi minor axis

8. Geoid
“A surface that closely approximates global mean sea level, but across
which pull of gravity is equal everywhere”.
• Geoids are lumpy and squat.
• Differences in densities causes variations in the
gravitational pull of Earth.
• Some geoid models are solved only for limited areas.
• Geoid + Ellipsoid = Earth

9. Datum or Reference System
• It is a set of mathematical (numeric and geometrical)
parameters or values to measure/describe spheroidal or
ellipsoidal objects.
• Consists of a series of numbers that define the shape and size
of the ellipsoid and it's orientation in space.
• A datum is chosen to give the best possible fit to the true shape
of the Earth.
• Geocentric or Earth Centered Datum:
Uses the Earth’s center of mass as the origin.
e.g. WGS 1984
• Geodetic or Local Datum:
Aligns its spheroid to closely fits the earth’s surface
e.g. NAD 1927 best for North American plate
Everest Datum (1830) used in Pakistan

10.  Horizontal Datum:
• Used for describing a point on the Earth's surface, in terms of
latitude and longitude or another coordinate system.
 Vertical Datum
• Orthometric Heights:
Based on Geoid (h)
• Ellipsoidal Heights:
Based on reference ellipsoid (H)
• Tidal Heights
Based on sea levels but most
common reference level is
Mean Sea Level (MSL)
• Used as a reference point for elevations of surfaces and
features on the Earth including terrain, water levels, and
man-made structures etc.
Datum is basically a reference either in horizontal or vertical, from which
distances or directions are measured

11. “An Earth coordinate system is the method of identifying the location of any point on Earth”.
Types of coordinate systems
1. Geographical Coordinate System
2. Projected Coordinate System
3. Global Cartesian Coordinate System
Earth Coordinate Systems

12. • Enables every location on Earth to be specified in three coordinates i.e. latitude (Ф), longitude (λ) and height (z)
• Locates object on the curved surface of Earth.
• Measured in degrees, minutes and seconds.
Describing Lines of latitude and longitude (From left to right) A person is standing in two
hemispheres
• Lines of Latitude parallel to equator
• Lines of Longitude perpendicular to the equator
• Prime meridian (meridian passes through Greenwich, England) and equator
are reference planes for Latitude and Longitude respectively.
1. Geographic Coordinate System (Ф, λ, z ):

13. • It is difficult to determine the length of latitude lines because they are concentric circles that
converge to single point at poles where the meridian begins.
• At equator, one degree of longitude 111.321kms
• At 60 degrees of latitude, one degree of longitude 55.802kms
• Which means there is no uniform length, hence the distance between points cannot
easily be measured using angular units of measure
Limitations of Geographical Coordinate System

14. 2. Projected Coordinate System (x, y, z)
• Define on a flat, two dimensional surface.
• Based on GCS (Spheroid GCS PCS)
• X axis representing East-West
• Y axis representing North-South
3. Global Cartesian Coordinate System (x, y, z)
• Specifies each point uniquely in a plane (Cartesian
plane) by a pair of numerical coordinates.
• Cartesian plane consists of:
• Two perpendicular axis that crosses a central point
called origin.
• East/West axis = x axis
• North/South axis = y axis
• Also called rectangular coordinates.

15. • The systematic transformation of points from the Earth’s surface to corresponding points on a
plane surface.
• Map projections are representations of a curved earth on a flat map surface.
• to corresponding points on a plane surface.
• Map projections are representations of a curved earth on a flat map surface.
Map Projection
Projection
conversion
formula from 3D
to 2 D
2D
Projected
Map

16. Types of Map Projection
1. Azimuthal /Planer Projection
2. Conic Projection
3. Cylindrical Projection

17. A map projection in which a region of the earth is projected on to a plane tangential to the surface, usually at
a pole or the equator.
1. Azimuthal / Planer Projection
Methods of Azimuthal /Planer Projection:
• Tangent Azimuthal Projection
• Secant Azimuthal Projection
Tangent Azimuthal Projection:
A plane is placed over the globe but touches at a single point.
Secant Azimuthal Projection:
A plane is placed over the globe but cuts the globe at two points.

18. Advantages and Disadvantages of Azimuthal Projection
Advantages:
• Intercept the Earth according to the different laws on perspectives.
• When the center of the projections is at the poles, the distances are real.
• It provides a great projection of the maps of the Arctic and the Antarctic, as well as of the hemispheres.
• The representation of the poles does not show distortion, because it increases at the equator.
Disadvantages:
• The distortion will be greater as the distance increases, from a point on the flat surface to the surface of the
balloon.
• It does not allow to represent the Earth in its totality, unless it presents distortions.

19. A map projection in which an area of the earth is projected on to a cone, of which the vertex is usually above
one of the poles.
2. Conic Projection
Methods of Conic Projection:
• Tangent Conic Projection
• Secant Conic Projection
Tangent Conic Projection:
A cone is placed over the globe but touches the globe surface at a single
point.
Secant Conic Projection:
A cone is placed over the globe but cuts the globe surface at two latitude
lines.

20. • Unlike cylindrical maps,
conic map projections are
generally not well-suited for
mapping very large areas.
They are more suitable for
mapping continental and
regional areas.
Advantages and Disadvantages of Conic Projection
• Distortion is evident near the top
and bottom of projection.
Continental or
Regional area

21. A map projection in which the surface features of a globe are depicted as if projected onto a cylinder
typically positioned with the globe centered horizontally inside the cylinder.
3. Cylindrical Projection
Methods of Cylindrical Projection:
• Tangent Cylinder
• Secant Cylinder
Tangent Cylindrical Projection:
A cylinder is placed over the globe but touches at a single point.
In this type, one standard parallel exist.
Secant Cylindrical Projection:
A cylinder is placed over the globe but cuts the globe at two
horizontal lines. In this type , two standard parallel exist.

22. • Accurate near the equator but distorts distances and sizes near the poles.
• Parallels and meridians form a grid, which makes locating positions easier.
• Shapes of small areas are usually well preserved.
Advantages and Disadvantages of Cylindrical Projection

23. Types of Azimuthal / Planer ,Conical and Cylindrical Projection

24. Advantages:
On Peter's projection, areas of equal size on the globe are also equally sized on the map.
Disadvantages:
Peter's chosen projection suffers extreme distortion in the polar regions, as any cylindrical projection must,
and its distortion along the equator is considerable.
Advantages and Disadvantages of Map Projection

25. Which is the best Projection?
• Accurate near the equator
• Parallels and meridians form a grid, which
makes locating positions easier
• Shapes of small areas are usually well
preserved
• Well suited for mapping large areas
 Cylindrical Projection is the best
in all Projections
Reasons:

26. Properties of Map Projection
• preserve shape
• shape preserved for local (small) areas
• sacrifices preservation of area away
• preserve area
• all areas are correctly sized relative to one another
• sacrifices preservation of shape serve distance
 Of the four projection properties, area and shape are
considered major properties and are mutually exclusive.
 No projection can retain more than one of these
properties over a large portion of the Earth.
 Conformal Projections
 Equivalent/Equal-Area Projections
 Equidistant Projections
• preserve distance
• preserve direction
 Azimuthal Projection

27. Geographic Transformation Method
Mathematical calculation that is used to convert
coordinates referenced from one datum to coordinates
referenced to another datum.

28. Geographic Transformation from datum NAD 27 to WGS 84

29. Geographic Transformation from datum WGS 84 to Clarke 1866

30. Geographic Transformation from datum WGS 84 to Clarke 1866

31. References
• http://slideplayer.com/slide/8398962/
• https://en.wikipedia.org/wiki/Cartesian_coordinate_system
• https://whatis.techtarget.com/definition/Cartesian-coordinates-rectangular-coordinates
• http://what-when-how.com/gps/datums-coordinate-systems-and-map-projections-gps-part-1/
• https://www.slideshare.net/riyagupta37819959/datum-29608582
• https://en.wikipedia.org/wiki/Geodetic_datum
• https://www.slideshare.net/TETL/geodesy-map-projections-introduction-presentation?next_slideshow=1
• https://www.e-education.psu.edu/natureofgeoinfo/c2_p14.html
• http://slideplayer.com/slide/5687395/
• https://lookaside.fbsbx.com/file/15-Datum-Projection_Shahid.pdf?token=AWxsARM-
MxZ8uR2qB_1LTrENxCDkRYirezqLX4m1BbK6jH6NEvV2dSZqYpGaJT1oAZmIOP3EB_E6MOLqQ9ZaA
7p9lvXV05Kh3qia6ffuG1lqdJ5n4XzuTSKEVpYAjCjYFNzuxid3cLe2JprLGc0s4cnu4KnutfEYy_nx8lQsbTTy
7A

32. • https://techinabottle.wordpress.com/2017/01/23/what-is-the-real-shape-of-earth/
• http://desktop.arcgis.com/en/arcmap/latest/map/projections/geographic-transformation-methods.htm