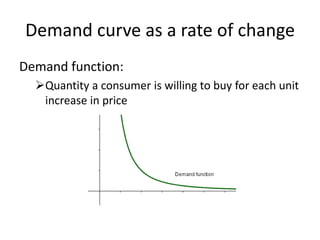
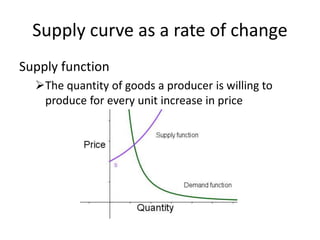
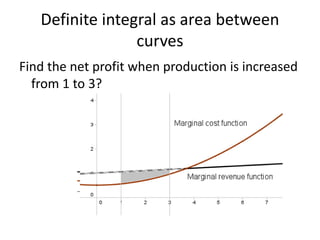
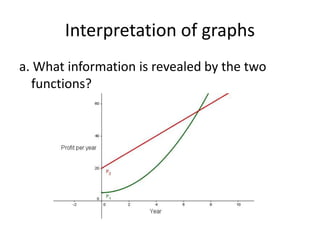
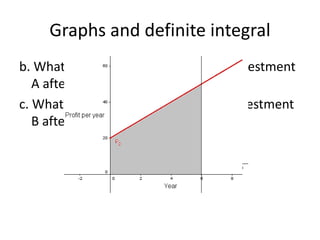
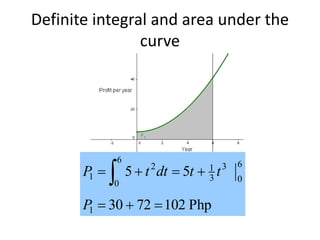
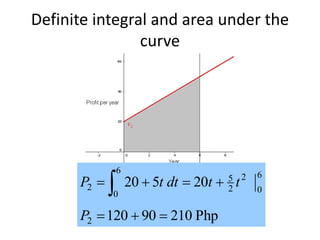
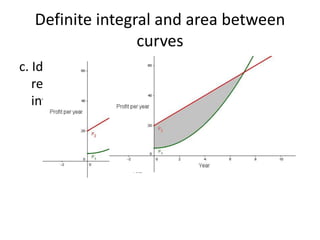
This document discusses the application of integration in business and economics. It provides examples of how integrals can be used to calculate total costs, profits, and areas between curves representing revenue and costs. Specifically: 1) Integrals allow calculating total costs by integrating marginal or incremental costs over quantity or time. 2) The difference between revenue and cost areas under their curves gives net profit over a range of quantities. 3) Investment profits over time can be found by taking the area under profit functions, allowing comparison of different investment options.

1. Application of Integration
Business and Economics

2. Derivative as rate of change
• Measurements described as a rate of change
is a derivative
• Key words:
Cost PER unit produced, profit PER unit sold
Cost FOR EVERY YEAR, value PER year
Marginal cost: additional cost for producing one
extra item of a product. Additional cost per unit of
production

3. Derivative as rate of change
Key words:
Marginal revenue: additional revenue by
increasing product sales by 1 unit: extra revenue
PER 1 unit increase in sales
Marginal profit: additional profit for each unit
sold: MP=MR-MC.

4. Demand curve as a rate of change
Demand function:
Quantity a consumer is willing to buy for each unit
increase in price

5. Supply curve as a rate of change
Supply function
The quantity of goods a producer is willing to
produce for every unit increase in price

6. Integral as Anti derivative
   dxxFxF '

 


axdxaC
adxdCa
dx
dC
COST PER UNIT PRODUCED

7. Integral as an antiderivative
Example 1.1
If cost of printing 1 book is 90 pesos, what is the
cost of printing 500 books?
xC
dxdC
dx
dC
90
9090

  
Php000,4550090
500At


C
x

8. Integral as antiderivative
If cost of printing 1 book is 90 pesos, what is the
cost of printing 500 books?
000,450000,45
9090
500
0
500
0

 
C
xdxC

9. Integral as antiderivative
Example 1.2
If the cost of producing 1 book unit is 90+0.01x,
what is the cost of producing 500 books?
dxxdCx
dx
dC
01.09001.090
500
0
  
Php250,46
200
000,250
000,45
2
90
500
0
2
100
1


x
xC

10. Integral as antiderivative
Example 1.3
In a certain factory the marginal cost of is
3(q-4)^2 when the level of production is q units.
How much would the total cost increase if
production is increased from 6 to 10?
   
 3
22
4
4343

  
qC
dqqdCq
dq
dC

11. Integral as antiderivative
Example 1.3
Increase in total cost when production is
increased from 6 to 10.
      dqqCC
2
10
6
43610  
 
Php208
8216264costTotal 3310
6
3

 q

12. Definite Integral as area between
curves
Example 1.4 (Area between curves)
If the marginal revenue from selling books is
And the marginal cost is
xR
dx
dR
05.01' 
 2
2'  xC
dx
dC

13. Definite integral as area between
curves
Find the net profit when production is increased
from 1 to 3?

14. Definite integral as area between
curves
  dxxdxxP
2
3
1
3
1
205.01  
 
 
 
Php22
13
2
205.01
5
1
5
1
3
1
40
1
3
1
40
9
3
1
3
3
12
40
1
2
3
1



 
xxx
dxxxP

15. Interpretation of graphs
Example 1.5 (Area between curves)
Suppose that t years from now, investment A
will generate a profit per year according to
While investment B will generate a profit per
year according to
  2
1 5' ttP 
  ttP 520'2 

16. Interpretation of graphs
a. What information is revealed by the two
functions?

17. Graphs and definite integral
b. What is the accumulated profit of investment
A after 6 years?
c. What is the accumulated profit of investment
B after 6 years?

18. Definite integral and area under the
curve
Php1027230
55
1
6
0
3
3
12
6
0
1

 
P
ttdttP

19. Definite integral and area under the
curve
Php21090120
20520
2
6
0
2
2
5
6
0
2

 
P
ttdttP

20. Definite integral and area between
curves
c. Identify the region in the graph which
represents the excess profit earned by
investment A over investment B over 6 years.

21. Definite integral and area between
curves
108729090
15515
5520
6
0
3
3
12
2
52
6
0
2
6
0
6
0





n
n
n
P
tttdtttP
dttdttP