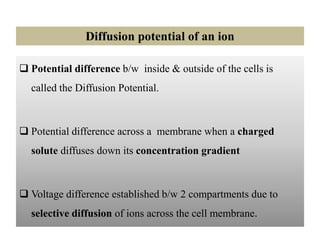
1. The document discusses the electrical properties of cell membranes, including diffusion potential, equilibrium potential, and the Donnan effect. 2. Diffusion potential is the voltage difference established across a membrane when ions diffuse down their concentration gradient through selective permeable pathways. The Nernst equation is used to calculate equilibrium potential for a single ion based on its intracellular and extracellular concentrations. 3. The Goldman equation calculates membrane potential based on permeability and concentrations of multiple permeable ions. 4. The Donnan effect refers to the uneven distribution of charged particles across a semipermeable membrane containing impermeable ions, maintaining concentration gradients and establishing a membrane potential.

1. LECTURE-39
Electrical properties of cell membrane -I
(Diffusion &Equilibrium Potential)
Dr Shamshad

2. Objectives
1. A:Define diffusion potential of an ion
B:Describe the mechanism of its generation
C:How it is calculated.
2. Explain the methods of calculation of equilibrium
potential when the membrane is permeable to several ions.
3. Define Donnan equilibrium and discuss its consequences
GUYTON & HALL Textbook of Medical Physiology, 12th edition, page: 57-58.

3. Diffusion potential of an ion
 Potential difference b/w inside & outside of the cells is
called the Diffusion Potential.
 Potential difference across a membrane when a charged
solute diffuses down its concentration gradient
 Voltage difference established b/w 2 compartments due to
selective diffusion of ions across the cell membrane.

4. What plays import role in generation of
Diffusion Potential
Electrical and Concentration gradients
Potential difference generated across the membrane when there is
an unequal diffusion of positive and negative ions.

5. Mechanism of generation

6. In Nerve fiber membrane:- [K+] > inside & < outside
Assume:- Membrane permeable to K+ ions only.
 Strong tendency for extra K+ ions leads to its diffusion
outward.
 Carry +ve electrical charges to the outside, thus
electropositivity outside the membrane & electronegativity
inside as negative anions remain behind.
 Within millisecond diffusion potential becomes great enough to
block further net K+ ions diffusion to the exterior, despite the
high K+ ion concentration gradient.
Normal N fiber, the potential difference = -94 mV, [ -ve inside]

7. Now Assume:-
 Membrane highly permeable to the Na+ ions only.
 Diffusion of the +vly charged Na+ ions to the inside creates a
membrane potential of opposite polarity with negativity
outside and positivity inside.
 Within milliseconds MP rises to block further net diffusion of
Na+ ions to the inside.
Nerve fiber potential +ve 61 mV inside the cell across the
selective permeable membrane.

8. Important Equations
I. Nernst equation:-Calculate the equilibrium potential for a
single ion, when we know its concentration inside & outside
the neuron.
It varies with temperature.
II. Goldman equation:-Calculate the rising potential of a neuron,
when we know the permeability to various ions.
Varies with ion concentrations.

9. Nernst equation
 Describes relation of Diffusion Potential to ion Concentration
difference across a Membrane.
 Diffusion potential across a membrane that exactly opposes
the net diffusion of a particular ion through the membrane is
called the Nernst potential for that ion.
 Two components used in the Nernst equations:-
1: Electrical force , 2: Diffusion force

10. Determined by:- Ratio of the concentrations of the specific ion
on the two sides of the membrane.
Greater this ratio, greater the tendency for the ion to diffuse in
one direction
Hence greater the Nernst potential required to prevent additional
net diffusion. Calculated at body temperature of 98.6°F (37°C)
Potential is positive (+) if the ion diffusing from inside to outside
is a -ve ion,
it is negative (−) if it is +ve ion .
Ex: when the concentration of K+ions on the inside is 10 times that on the outside, the
log of 10 is 1, so the Nernst potential calculates to be −61 millivolts inside the
membrane.

11. Nernst equation
 Used to calculate the equilibrium potential for an ion at a
given concentration difference across the membrane.
EMF = Electromotive (mV)
Z=ionic valence of given ions (charge+/-)
Concentration inside
And outside =intracellular concentration
for a given ions (mmol/l)

12. Ex: If the intracellular [Ca2+] is 10−7 mol/L and the extracellular
[Ca2+] is 2 × 10−3 mol/L, at what potential difference across the
cell membrane will Ca2+ be at electrochemical
equilibrium? Assume that 2.3RT/F = 60 mV at body temperature
(37°C).
SOLUTION. Given this concentration gradient across the
membrane, if Ca2+ is the only permeant ion. Remember, Ca2+ is
divalent, so z = +2.
Thus,

13. The Goldman Equation
 When a membrane is permeable to several different ions, the
diffusion potential that develops depends on three factors:
(1) Polarity of the electrical charge of each ion,
(2) Permeability of the membrane (P) to each ion,
(3) Concentrations (C) of the respective ions on the inside (i) and
outside (o) of the membrane.
 Goldman equation or the Goldman-Hodgkin-Katz equation, gives
the calculated membrane potential on the inside of the membrane
when two univalent positive ions, sodium (Na+) and potassium
(K+), and one univalent negative ion, chloride (Cl−), are
involved.

14. Donnan Effect
 The Gibbs-Donnan Equilibrium/Donnan Equilibrium:-is basis for
electrical charges that are found across the membranes of many
cells. (Ex: Nerve & Muscle cells).
 It refers to the uneven distribution of charged particles on one side
of a semipermeable membrane.
 These particles are not able to evenly distribute themselves by
diffusion across both sides of the membrane.
 The Donnan Effect is the “phenomenon of predictable and
unequal distribution of permeable charged ions on either side of a
semipermeable membrane, in the presence of impermeant charged
ions”.

15. Mechanism of Donnan Equilibrium
 When two solutions of differing concentrations are separated by a
semipermeable membrane their concentrations will equalize by
diffusion.
 But If there is an impermeable solute in one of the solutions, the
concentration of the solution does not equalize.
 The concentration of the solution with impermeable solutes remains
high even at equilibrium.
 This effect is called the Donnan equilibrium.
passive process

16.  Cell membranes of living cells are selectively permeable.
 Donnan effect regulate flow of molecules & ions b/w cell
and its environment.
 Living cells contain impermeable anionic colloids,
(ex:-proteins & organic phosphates)
 Colloidal anions cannot cross the cell membrane.
 Leading to high concentration of non-diffusible anions
across the cell membrane,
this creates the Donnan Equilibrium.
 The presence of impermeant ions on one side of the
membrane creates an osmotic diffusion gradient attracting
water into that compartment
 If this process continues, the cells will inevitably rupture.

17.  Presence of the sodium pump (Na⁺- K⁺ ATPase) prevent
cells from rupturing by continuously pushing out excess ions.
 The pump together with the membrane’s low permeability to
Na+ effectively prevents Na+ from entering the cell.
 The sodium pump renders the membrane impermeable to Na+,
setting up Donnan Equilibrium.

19. At equilibrium two things happen:-
I. The diffusible [K+] ions on the side of the membrane
containing the non-penetrating anion X- is greater than the
diffusible cation concentration on the other side
II. The diffusible anions [cl-] ions will be greater on the side
without the non-diffusible anion.
This is known as the Gibbs –Donnan membrane equilibrium

20. It’s consequences
 The asymmetrical distribution of ions across the cell
membrane at equilibrium has the following effect on the
body.
 There will be an electrical difference across the cell
membrane whose magnitude can be measured by the
Nernst equation
 Because of protein anions in the cells there are more
osmotically active particles in the cells than the interstitial
fluid.
 This would make them swell and eventually rupture , but
prevented b operation of Na+-K+ which produce the net
+ve charge out of the cell and keep the inside and outside
osmotic equilibrium.