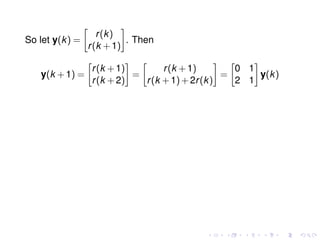Download as PDF, PPTX
Uploaded byMatthew Leingang
PDF, PPTX1,236 views
Lesson32 Second Order Difference Equations Slides
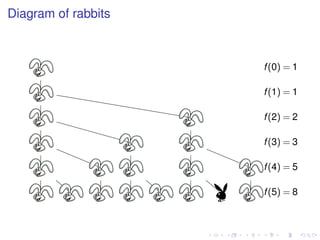
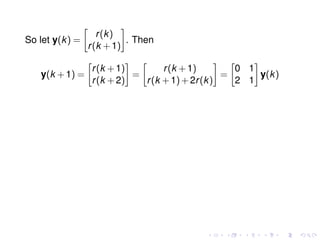
This document discusses solving second-order difference equations by treating them as systems of first-order equations. It provides the example of the Fibonacci sequence, defined by f(k+2)=f(k)+f(k+1), and shows how to set it up as the system y(k+1)=Ay(k) where y(k)=[f(k) g(k)]^T. The eigenvalues and eigenvectors of the matrix A are found, allowing the solution to be written as a combination of terms involving the eigenvalues. The constants are then determined using the initial conditions to obtain the final solution for f(k).
![Week 3 [compatibility mode]](https://cdn.slidesharecdn.com/ss_thumbnails/week3compatibilitymode-130213164415-phpapp02-thumbnail.jpg?width=640&height=640&fit=bounds)
