The document discusses matrices and their types and applications. It defines a matrix as a rectangular arrangement of numbers, expressions or symbols arranged in rows and columns. It describes 10 different types of matrices including row, column, square, null, identity, diagonal, scalar, transpose, symmetric and equal matrices. It also discusses three algebraic operations on matrices: addition, subtraction and multiplication. Finally, it provides examples of how matrices are used in economics to calculate costs of production, in geology for seismic surveys, and in robotics and automation to program robot movements.

2. MOHAMMAD AKASH
ID:029
FATEMA TABASSUM
ID:027
JOYONTO MALLIK
ID:002
SHUVRO BANIK
ID:011
ESHITA YESMIN
ID:035
KARTIK SARMA
ID:043

3. It is an collection of element which is arranges in rows and columns
MATRIX
It is the combination of linear equation
It is represented by these symbols : () , [] , l l

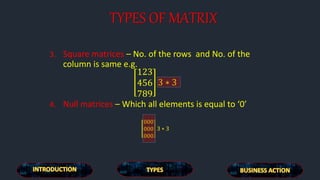
4. TYPES OF MATRIX
1. Row matrices – A matrices which has only one row
called row matrices e.g.-
[123]1*3
2. Column matrices – A matrices which has only one
column is called column matrices e.g. –
1
2
3
3 ∗ 1

5. TYPES OF MATRIX
3. Square matrices – No. of the rows and No. of the
column is same e.g.
123
456
789
3 ∗ 3
4. Null matrices – Which all elements is equal to ‘0’
000
000
000
3 ∗ 3

6. TYPES OF MATRIX
5. Identity matrices – A square matrices who’s main diagonal is
assinty value ‘1’ and each of the other element is ‘0’
e.g
100
010
001
3 ∗ 3 ,
10
01
2 ∗ 2, 1 1 ∗ 1
5. Diagonal matrices – A square matrices all of who’s element
expect those in the leading diagonal are ‘0’ e.g. -
100
050
009
3 ∗ 3

7. TYPES OF MATRIX
7. Scalar matrices – A diagonal matrices in which all the elements of
main diagonal is same called scalar matrices e.g.- 200
020
002
3*3
8.Transpose Matrices – A matrices obtained by inter
changing the rows and columns of a matrices A It is
denoted by A’ , AT e.g.:-
A⇒
123
456
789
3 ∗ 3 AT ⇒
147
258
369
3 ∗ 3

8. TYPES OF MATRIX
9. Symmetric Matrices - A square matrices A is called symmetric matrices if
it is equal to its transpose e.g.-𝐴 ⇒
100
010
001
3 ∗ 3, 𝐴′
⇒
100
010
001
3 ∗ 3
10.Equal Matrices – If two matrices order and there corresponding element
is same is called equal matrices
If X⇒
2 3
4 5
2 ∗ 2 𝑎𝑛𝑑 𝑌 ⇒
2 3
4 5
2 ∗ 2

9. TYPES OF MATRIX
11.Algebraic Matrices – There are three type:-
i. Addition method - for addition of two matrices the order must be same e.g.:-
A⇒
3 −2
1 −4
2 ∗ 2, 𝐵 ⇒
3 −1
4 6
2 ∗ 2
𝐴 − 𝐵 ⇒
3 −2
1 −4
+
3 −1
4 6
⇒
3 + 3 −2 + −1
1 + 4 −4 + 6
⇒
6 −3
5 2
2 ∗ 2

10. TYPES OF MATRIX
ii. Subtraction method –For subtraction of two matrices the order
must be same.
Example:-
A⇒
3 2 1
6 2 3
4 8 9
3 ∗ 3, 𝐵 ⇒
5 6 −2
1 −2 −3
3 4 7
3 ∗ 3
A-B⇒
3 2 1
6 2 3
4 8 9
−
5 6 −2
1 −2 −3
3 4 7
⇒
3 − 5 2 − 6 1 − −2
6 − 1 2 − −2 3 − −3
4 − 3 8 − 4 9 − 7
⇒
−2 −4 3
5 4 6
1 4 2

11. TYPES OF MATRIX
iii. Multiplication of method –
Example:-
and
Then,

12. TYPES OF MATRIXLet,
and
Compute AB.
Solution: The size of matrix A is 2x3, and the size of matrix B is 3x3. Since the number of columns of matrix A is equal
to the number of rows of matrix B, the matrix product C = AB is defined. Furthermore, the size of matrix C is 2x3.
Thus,

13. TYPES OF MATRIX
It remains now to determine the entries c11, c12, c13, c21, c22 and c23. We have
So the required product AB is given by

14. ACTION OF MATRIX
Matrix Multiplication in Economics
We gave you an example of how matrix multiplication could be used in math itself, but how about in real life, what
benefit can it provide to us? Well, The basic principle for the example concerns the cost of producing several units of
an item when the cost per unit is known.
{Number of units} * {Cost per unit} = {Total cost}
Example
A company manufactures two products. For $ 1.00 worth of product A, the company spends $ .40 on materials, $.20
on labor, and $.10 on overhead. For $1.00 worth of product B, the company spends $.30 on materials, $.25 on labor,
and $.35 on overhead. Suppose the company wishes to manufacture x1 dollars worth of product A and B. Give a
vector that describes the various costs the company will have to endure?

15. ACTION OF MATRIX
Step 1
.40 .30
A = .20 and B = .25
.10 .35
Step 2
The cost of manufacturing x1 dollars worth of A are given by x1*A and the costs of
manufacturing x2 dollars worth of B are given by x2.B. Hence the total costs for both
products are simply given by their products once again,
.40 .30
[ x1 ] .20 + [ x2 ] .25 = x1*A + x2*B.
.10 .35

16. ACTION OF MATRIX
In geology, matrices are used for taking seismic surveys.
They are used for plotting graphs, statistics and also to do scientific studies in almost different fields.
• Matrices are used in representing the real world data’s like the traits of people’s population, habits, etc.
They are best representation methods for plotting the common survey things.
• Matrices are used in calculating the gross domestic products in economics which eventually helps in
calculating the goods production efficiently.
• Matrices are used in many organizations such as for scientists for recording the data for their experiments.
• In robotics and automation, matrices are the base elements for the robot movements.
The movements of the robots are programmed with the calculation of matrices’ rows and columns.
The inputs for controlling robots are given based on the calculations from matrices.

17. conclution
 Matrices are nothing but the rectangular arrangement of numbers, expressions, symbols which are
arranged in columns and rows.
 The numbers present in the matrix are called as entities or entries.
 A matrix is said to be having ‘m’ number of rows and ‘n’ number of columns.
 Matrices find many applications in scientific fields and apply to practical real life problems as
well, thus making an indispensable concept for solving many practical problems.

18. Thank you!
MATRIX AND IT'S BUSINESS APPLICATION