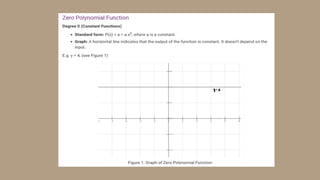
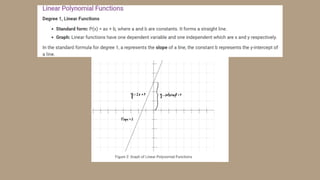
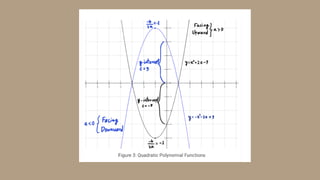
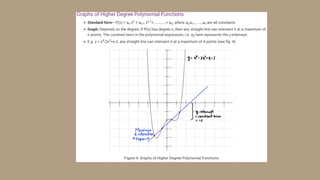
This document discusses polynomial functions including: 1) Identifying polynomials and their degree, evaluating polynomials using synthetic substitution, illustrating polynomial equations, and solving problems involving polynomials. 2) Defining a polynomial function as a function involving only positive integer exponents of a variable and noting the highest power as its degree, with the domain being all real numbers. 3) Providing examples of types of polynomial functions and graphs of polynomial functions, and evaluating polynomials using direct substitution or synthetic substitution.

1. POLYNOMIAL FUNCTIONS

2. Lesson Objectives:
identify polynomials and their degree
evaluate polynomials using synthetic substitution
illustrate polynomials equations and;
solve problems involving polynomials
In this lesson, you will be able to :

3. Pre-assessment
What do 2x³+x+3, 34x²-2x+134, and 34 have in
common?

4. Definition:
A polynomial function is a function that involves only positive integer
exponents of a variable.
The highest power of the variable of P(x) is known as its degree.
The domain of a polynomial is the entire real numbers (R).

5. Examples:

6. Types of Polynomial Functions

7. Graphs of Polynomial Functions

13. Evaluating Polynomial Functions
Direct substitution:
When you evaluate an expression for a given value, you
substitute that given value in the expression, and find its
numerical value.

15. Let's Practice!

16. Evaluating Polynomial Functions
Synthethic Substitution
Steps:
1.Write the coefficients of the polynomial in a row. Make
sure that the polynomial function is arranged in
descending order. You must include a zero coefficient for
missing term of the polynomial.
2.Perform the synthetic division.

17. Evaluating Polynomial Functions
3. Apply the Remainder Theorem which says, “If a
polynomial f(x) is divided by x – c, then the remainder is
f(c).” Simply put, the Remainder Theorem says if you want
to evaluate a polynomial at some value c, then the answer
is the remainder.

19. Let's Practice!