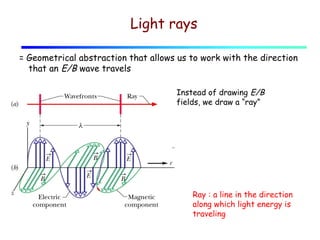
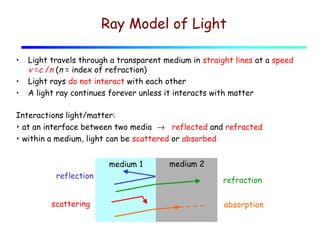
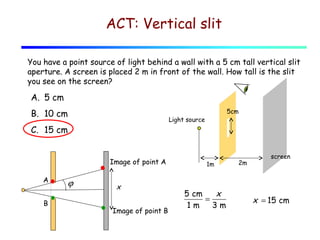
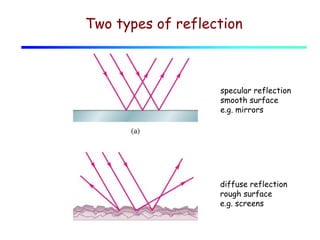
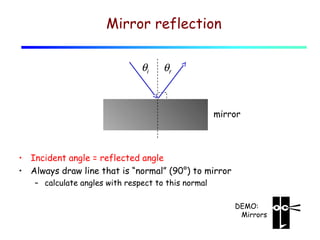
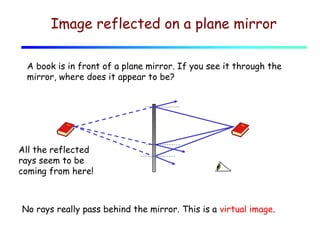
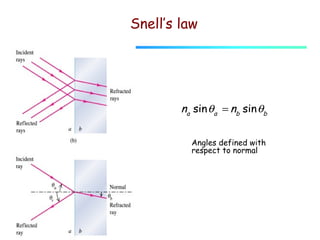
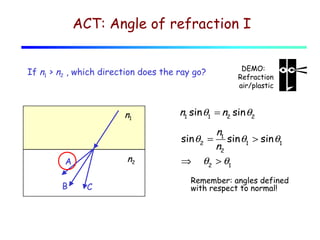
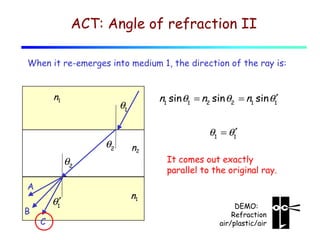
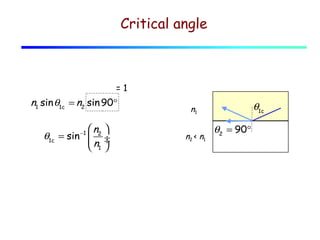
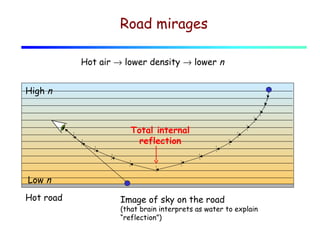
This document provides an introduction to geometric optics and concepts of reflection and refraction of light. It discusses how light rays interact with surfaces and change direction at boundaries between different optical media based on Snell's law. Total internal reflection is described, in which light reflecting back into the original medium if the angle of incidence is greater than the critical angle. Applications like fiber optics and mirages are discussed. A simple model is provided of light propagation through materials involving absorption and re-emission of photons by atoms.

1. Lecture 33
Reflection and refraction.

2. Introduction to geometric optics
Select an object of your choice (table, book, coin,
neighbor’s head). Think about and discuss:
• what it means to “see it”
→ EM waves (light) from lamps hit surface and are reflected.
→ Waves propagate spherically in all directions from object.
→ Your eye is sensitive to light
• how you perceive the position of that object
→ brain “traces back” to where the light comes from.
→ 3D perception comes from brain comparing images from each eye.

3. Light rays
= Geometrical abstraction that allows us to work with the direction
that an E/B wave travels
Instead of drawing E/B
fields, we draw a “ray”
Ray : a line in the direction
along which light energy is
traveling

4. Ray Model of Light
•
•
•
Light travels through a transparent medium in straight lines at a speed
v =c /n (n = index of refraction)
Light rays do not interact with each other
A light ray continues forever unless it interacts with matter
Interactions light/matter:
• at an interface between two media → reflected and refracted
• within a medium, light can be scattered or absorbed
medium 1
reflection
scattering
medium 2
refraction
absorption

5. ACT: Vertical slit
You have a point source of light behind a wall with a 5 cm tall vertical slit
aperture. A screen is placed 2 m in front of the wall. How tall is the slit
you see on the screen?
A. 5 cm
B. 10 cm
Light source
C. 15 cm
Image of point A
A
B
ϕ
5cm
x
Image of point B
1m
5 cm
x
=
1m
3m
2m
screen
x = 15 cm

6. Two types of reflection
specular reflection
smooth surface
e.g. mirrors
diffuse reflection
rough surface
e.g. screens

7. Mirror reflection
θi
θr
mirror
• Incident angle = reflected angle
• Always draw line that is “normal” (90°) to mirror
– calculate angles with respect to this normal
DEMO:
Mirrors

8. Image reflected on a plane mirror
A book is in front of a plane mirror. If you see it through the
mirror, where does it appear to be?
All the reflected
rays seem to be
coming from here!
No rays really pass behind the mirror. This is a virtual image.

9. How to find the image
• Draw two rays (one of them the normal to the surface, it’s a
trivial one)
• Draw reflected rays.
• Extrapolate rays until they intersect.
Plane mirror:
s = -s’
s’
s
s : location of the object
Positive in front of mirror
s’: location of the image
Negative behind mirror

10. EM waves not in vacuum
Phys 221:
E field inside a material is characterized by dielectric
constant κ or the dielectric permittivity ε = κε 0
Similarly:
B field inside a material is characterized by relative
permeability κm or the permeability µ = κ m µ0 (often κ m : 1)
EM wave speed in a dielectric:
v =
1
εµ
=
c
κκ m
c
=
n
n = κκ m
(>1
always )
Refraction index

11. Refraction
Fact: Light changes direction when it crosses a boundary
Reason: Speed of light is different in both media
– At boundary, part of wavefront is in slower media
– Travels shorter distance in ∆t
slower

12. Snell’s law
na sin θa = nb sin θb
Angles defined with
respect to normal

13. ACT: Angle of refraction I
If n1 > n2 , which direction does the ray go?
n1
DEMO:
Refraction
air/plastic
n1 sin θ1 = n2 sin θ2
n1
sin θ1 > sin θ1
n2
θ2 > θ1
sin θ2 =
n2
A
B
C
⇒
Remember: angles defined
with respect to normal!

14. ACT: Angle of refraction II
When it re-emerges into medium 1, the direction of the ray is:
n1
n1 sin θ1 = n2 sin θ2 = n1 sin θ1′
θ1
θ2
θ1 = θ1′
n2
θ2
A
B
θ1′
C
n1
It comes out exactly
parallel to the original ray.
DEMO:
Refraction
air/plastic/air

15. In-class example: Refraction
A ray of light strikes the interface between air and an unknown
substance at an angle θ1 = 75° from the normal to the surface. The
refracted beam makes an angle θ2 = 30° from the normal. What is
the index of refraction of this substance?
A. 2.5
75°
75°
B. 1.9
C. 1.3
30°
air
X
D. 1.0
E. 0.50
Impossible, n ≥ 1
= 1.0
nair sin 75° = nX sin30°
nX =
sin 75°
= 1.9
sin30°

16. Total internal reflection
As light goes to a medium with lower n, the angle from the
normal increases (θ1 < θ2):
θ1
n1
n2 < n1
θ2
θ1
θ2
θ1c
θ1
θ2
If θ1 is large enough, θ2 = 90° !!
Beyond this angle, there is no more refraction, only reflection.
DEMO:
Total internal
reflection

17. Critical angle
=1
n1 sin θ1c = n2 sin 90°
 n2
θ1c = sin 
n
 1
−1

÷
÷

θ1c
n1
n2 < n1
θ2 = 90°

18. Fiber optics
cladding
core
Both cladding and core are glass such that ncore > ncladding
Light internally reflects within the inner glass fiber
– no refracted ray going outside
– minimal light loss
DEMO:
Water tank.
Fiber optics

19. Road mirages
Hot air → lower density → lower n
High n
Total internal
reflection
Low n
Hot road
Image of sky on the road
(that brain interprets as water to explain
“reflection”)

20. Light through matter: a simple model
What does really happen when light travels through matter?
It depends on how you want to think about it.
atom
You can say that the photons occasionally
interact with atoms in a dielectric, being
absorbed and re-emitted, and that this only
appears to slow them down. Here, the
photons travel at “c”.
v=c
v=c
absorb & re-emit
with some phase
delay
Or you can say that the wave that propagates through the solid is a
combination of a photon and virtual excitations of the atoms of the solid.
This wave travels with v < c.

21. What defines a color?
So the atom oscillates with the frequency of the radiation
and then re-emits.
→ Frequency remains the same
→ Wavelength changes
n1
v1
c
λ1 = =
f n1f
n2 < n1
v2
c
λ2 = =
> λ1
f n2f
“Color” correspond to a fixed frequency. The wavelength
depends on the medium.