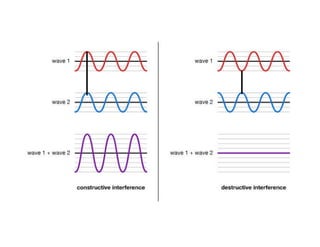
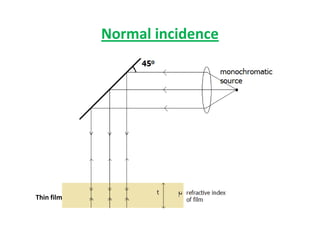
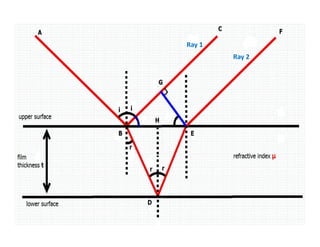
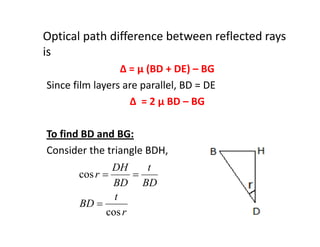
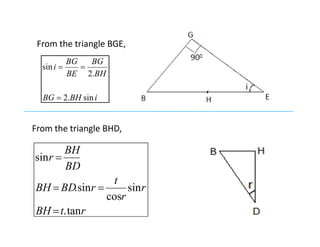
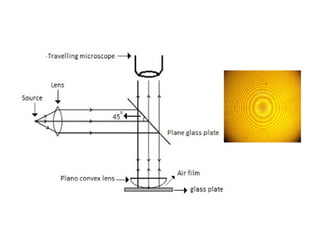
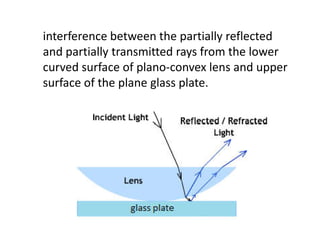
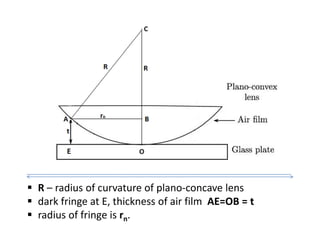
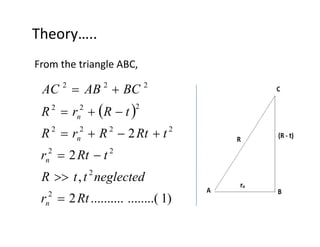
The document discusses thin film interference and Newton's rings, explaining the principles of constructive and destructive interference based on path differences between waves. It highlights the conditions under which these interference patterns occur, utilizing concepts such as coherence, monochromatic light, and optical path differences. Additionally, it describes Newton's study of ring patterns formed by interference of light from a plano-convex lens and a glass plate, along with the mathematical relationships that govern these phenomena.

1. Thin film interference and
Newton's ringNewton's ring
Muhammed Abdurahman K
Physics, M.E.S Ponnani College

2. Interference
• Interference - phenomenon in which two waves superpose
to form a resultant wave of greater, lower, or the same
amplitude
• Principle of superposition:-
when two or more waves of the same type superimposes,
the resultant displacement will be the algebraic sum of the
displacements due to each individual wave
Superposition of two waves with displacement y1 and y2 is
21 yy

y

3. constructive and destructive
• Constructive interference occurs when the wave
amplitudes reinforce each other, building a wave
of even greater amplitude
– Path difference = n.λ with n = 0,1,2,…– Path difference = n.λ with n = 0,1,2,…
• Destructive interference occurs when the wave
amplitudes oppose each other, resulting in waves
of reduced amplitude
– Path difference = (2n+1).λ/2 with n = 0,1,2,…

5. • Coherence - two wave sources are perfectly
coherent, if they have
– constant phase difference
– same frequency,
– same waveform– same waveform
• Monochromatic light –
– wave with single frequency (single colour)

6. Thin film
• Thin film –
– Soap film
– Film of oil spread on water surface
• thickness – few micro meters• thickness – few micro meters
• Waves reflected from upper surface interfere
with waves reflected from lower surface
– Normal incidence
– Oblique incidence

7. Normal incidence
Thin film

8. • Light reflected from lower surface has an optical path
difference of 2μt to interfere with light reflected from
upper surface.
• Also the light reflected from upper surface undergo a• Also the light reflected from upper surface undergo a
path difference of λ/2
• Effective path difference between two rays is,
Δ = 2μt - λ/2

9. • If the path difference is integral multiple of λ,
constructive interference occurs and appears to be
bright.
2μt - λ/2 = n λ, with n = 0,1,2,…..
for bright, 2μt = (n + ½).λ
• If the path difference is odd multiple of λ/2, destructive
interference occurs and appears to be dark.
2μt - λ/2 = (2n + 1) λ/2, with n = 0,1,2,…..
for dark, 2μt = nλ

10. Oblique incidence
• Thin film with uniform thickness ‘t’ and
refractive index μ
• Monochromatic light with wave length λ
• Incident angle - i• Incident angle - i
• Refracted angle - r
• Reflected rays from upper and lower surfaces
are coherent (derived from a single source)
and superimposes to produce interference.

11. Ray 1
Ray 2

12. Optical path difference between reflected rays
is
Δ = μ (BD + DE) – BG
Since film layers are parallel, BD = DE
Δ = 2 μ BD – BG
To find BD and BG:
Consider the triangle BDH,
r
t
BD
BD
t
BD
DH
r
cos
cos



13. iBHBG
BH
BG
BE
BG
i
sin.2
.2
sin


From the triangle BGE,
From the triangle BHD,From the triangle BHD,
rtBH
r
r
t
rBDBH
BD
BH
r
tan.
sin
cos
sin.
sin




14. r
r
tr
r
r
tBG
i
r
r
tBG
ri
r
i
cos
sin
..2sin..
cos
sin
..2
sin.
cos
sin
..2
sin.sin,
sin
sin
2





There fore the path difference, Δ = 2 μ BD – BG
rtr
r
t
r
r
t
r
t
cos..2cos.
cos
..2
sin
cos
..2
cos
..2
2
2






15. Optical path difference between the superimposed
rays is
Δ = 2.μ.t. cos r
Light reflected from upper surface undergo a pathLight reflected from upper surface undergo a path
difference of λ/2
Effective path difference between two rays is,
Δ = 2 μ t cos r - λ/2

16. • If the path difference is integral multiple of λ,
constructive interference occurs and appears to be
bright.
2 μ t cos r - λ/2 = n λ, with n = 0,1,2,…..
for bright, 2 μ t cos r = (n + ½).λ
• If the path difference is odd multiple of λ/2,
destructive interference occurs and appears to be
dark.
2 μ t cos r - λ/2 = (2n + 1) λ/2, with n = 0,1,2,…..
for dark, 2 μ t cosr = nλ

17. Colours of thin film

18. Due to interference…
• Thin film interference depends on
– thickness of film
– angle of incidence (or refraction)
• Observer views different region of film at different
angles, depending on angle and thickness of film a
particular wavelength of white light may satisfy the
condition for constructive or destructive interference.condition for constructive or destructive interference.
• Colour satisfy constructive interference present in that
region, and colour satisfy destructive interference is
absent.
• Different points on the film appear in different colours
depending on angle of reflected light coming to
observers eye from that point.

19. Newton's rings
• In 1717, Sir Isaac Newton studied the rings
pattern generated due to interference of light
• monochromatic and coherent rays i.e. rays of
same frequency and constant phasesame frequency and constant phase
difference
• appears as a series of concentric, alternate
bright and dark rings centred at the point of
contact

21. interference between the partially reflected
and partially transmitted rays from the lower
curved surface of plano-convex lens and upper
surface of the plane glass plate.

22.  R – radius of curvature of plano-concave lens
 dark fringe at E, thickness of air film AE=OB = t
 radius of fringe is rn.

23. Theory…..
From the triangle ABC,
 222
222
tRrR
BCABAC
n 

)1........(..........2
,
2
2
2
2
22
2222
Rtr
neglectedttR
tRtr
tRtRrR
n
n
n





24. Condition for dark fringe is, 2 μ t cosr = nλ
For air film, μ = 1
For normal incidence, r = 0
2 t = nλ ………………(2)
From equations (1)&(2),
RntRD
rDdiameter
Rnr
Rnr
n
nn
n
n
..2..22
2,
..
..2








25. Since thickness of air film at centre is zero, the path
difference will be zero to get a dark spot.
)3.(.......................4
2,
..
2
2
RnD
rDdiameter
Rnr
n
nn
n





For (n+k)th dark ring,   )4.........(...42
RknD kn 
Rk
DD
RkDD
nkn
nkn
..4
...4
22
22







Difference between equations (3)&(4) is
Wavelength of mono-
chromatic light,

26. 9496314879
abdurahman.physics@gmail.com