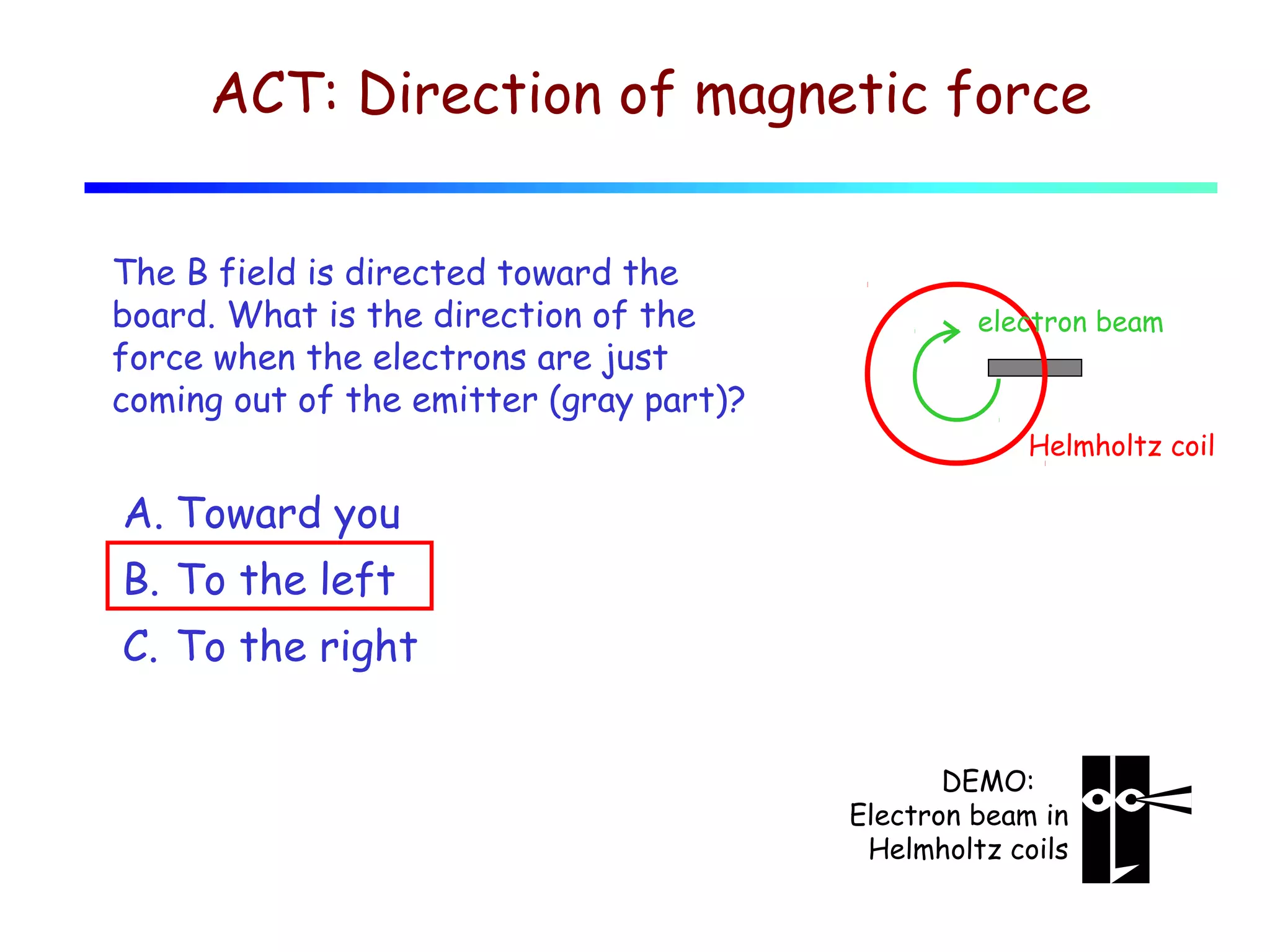
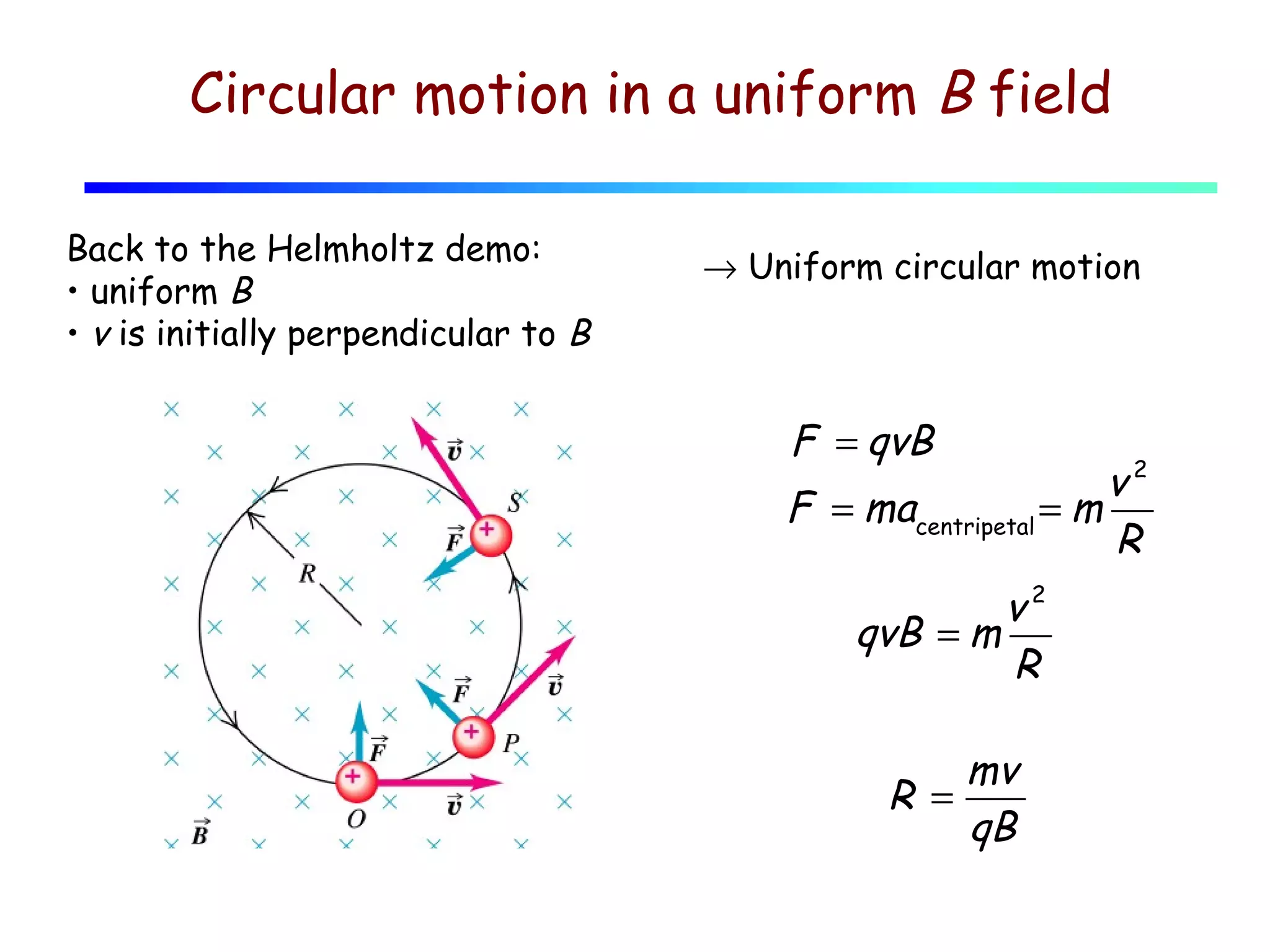
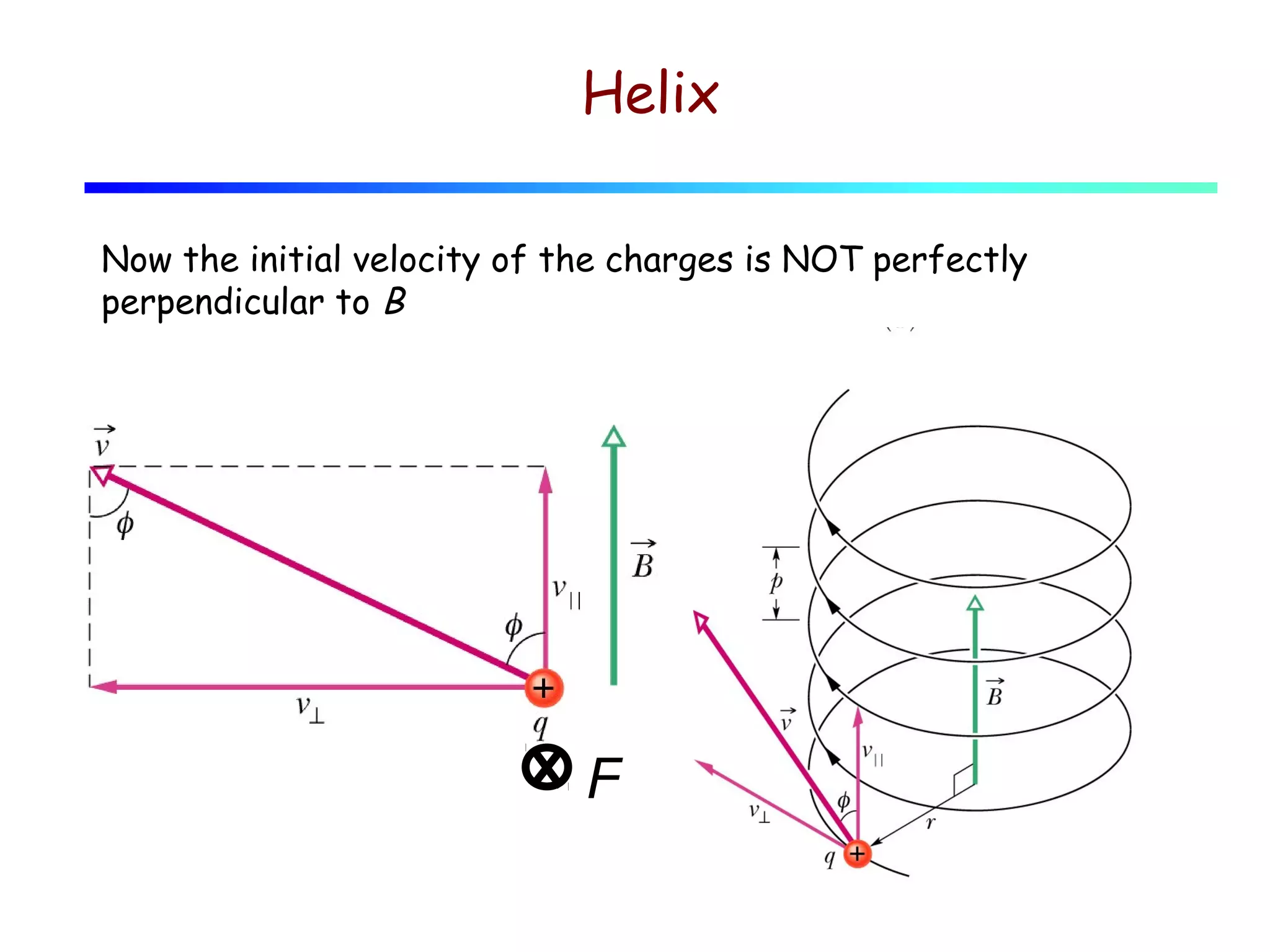
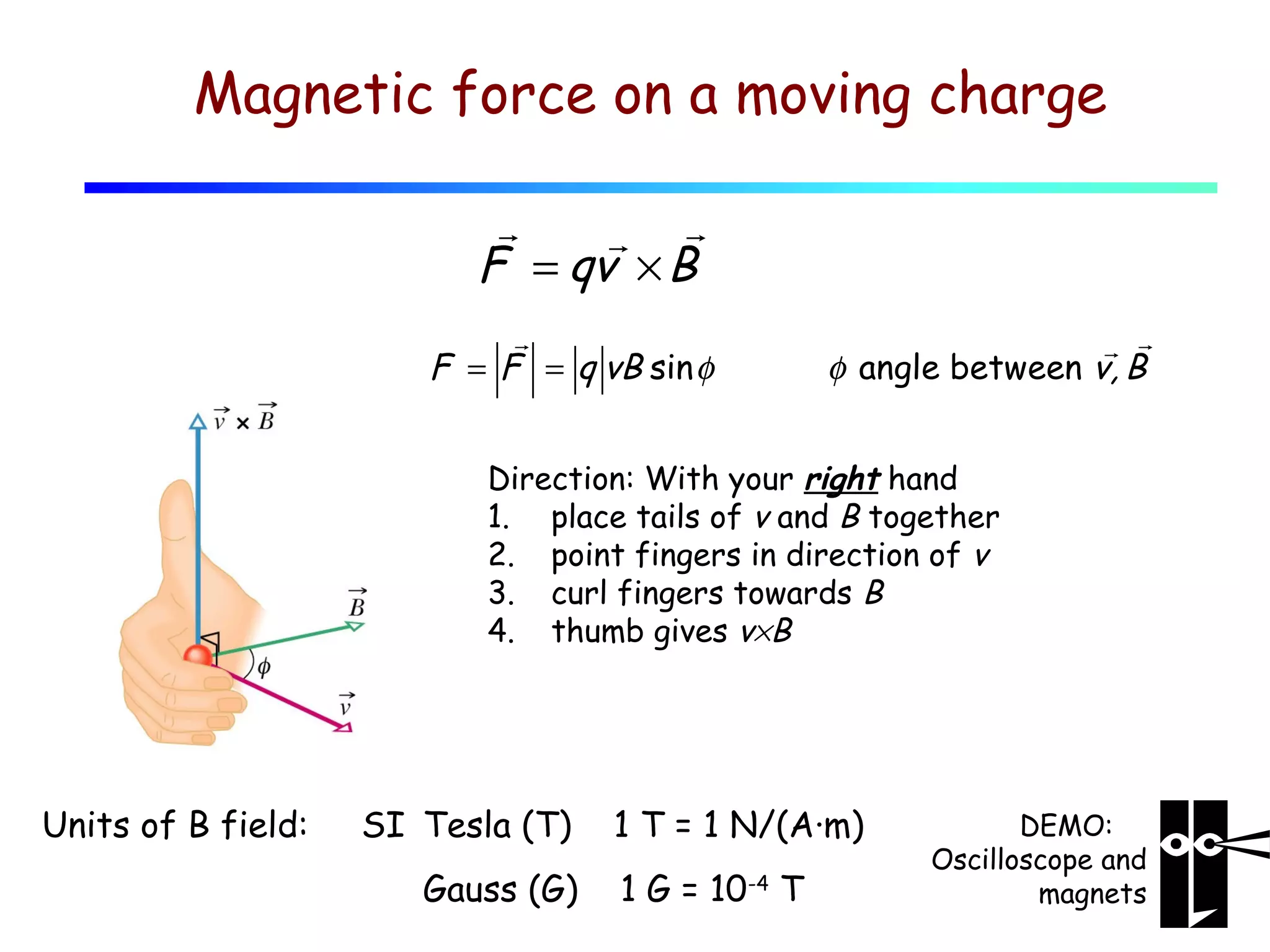
1) The document discusses magnetic fields, field lines, and the forces experienced by moving charges in magnetic fields. 2) It explains that a magnetic field extends through all space and is represented by magnetic field lines. A magnetic dipole field leaves the North pole and enters the South pole. 3) The magnetic force on a moving charge is perpendicular to both the magnetic field and the velocity of the charge, and is given by the equation F=qv×B.

1. Lecture 20
Magnetic fields, field lines,
moving charges.

2. Quick reminder: E field
Phys 221: Electric force between two charges
r
F =
1 q1q2
ˆ
r
4πε 0 r 2
Huge question: How is this force communicated over a distance?
How does charge 2 know about charge 1?
Partial answer: Charge 1 sets up an electric field
If a second charge is placed in electric field
then it experiences a force
r
r
F = qE
Remarkable conceptual leap…
Electric field extends over ALL space
If charge 1 moves, field changes

3. Magnetic field B
Similarly a magnet sets up a magnetic fieldB
In a few weeks time we will show that it is the moving charges
(electrons in atomic orbitals) that create the B-field
For now we will assume we can somehow create a B-field and look at
the force it exerts on charged particles
B-field
• extends to all points in space
• at every point, there is a vector B that has a particular magnitude
and direction
• magnetic field lines: like E-field lines:
• B-field is tangent to them at all points
• magnitude of B-field is indicated by the density of lines

4. Magnetic dipole field
B-field leaves N-pole and go to S-pole
B-field is continuous,
no monopoles
(“magnetic charge”)
– There is nothing special about a “pole”: it’s just where the material ends

5. Build from the basics
• For now, build from basics
– Magnetic force experienced by a single moving charge in a preexisting B-field
• Next week
– How to create a B-field from a moving charge
• Few weeks time
– Interaction between two current loops
• Reason why iron is attracted to magnets

6. ACT: Direction of magnetic force
The B field is directed toward the
board. What is the direction of the
force when the electrons are just
coming out of the emitter (gray part)?
electron beam
Helmholtz coil
A. Toward you
B. To the left
C. To the right
DEMO:
Electron beam in
Helmholtz coils

7. Weird
The magnetic force on a particle is perpendicular to B-field
F
B
e-
Very different to E-field, where
F is parallel to E
r
r
Felectric = qE
v
The motion is circular: F changed
direction as v changed direction
Magnetic force is also
perpendicular to v
Also, magnetic force is observed to be
• proportional to the charge
• flip direction if charge of opposite sign is
used
F
B
v
e-

8. Magnetic force on a moving charge
r
r r
F = qv × B
r
F = F = q vB sin φ
r r
φ angle between v, B
Direction: With your right hand
1. place tails of v and B together
2. point fingers in direction of v
3. curl fingers towards B
4. thumb gives v×B
Units of B field:
SI Tesla (T)
Gauss (G)
1 T = 1 N/(A·m)
1 G = 10-4 T
DEMO:
Oscilloscope and
magnets

9. ACT: Magnetic force
What is the direction of the magnetic field if this is the force it
produces on the moving negative charge?
A.
B.
C.
+x
−x
Other
r
F
r
B

10. Noteworthy
r
r r
F = qv × B
Hmm. Then what if I look
at this from a different
reference frame?
• No force on a stationary charge
• No force on a charge that moves parallel to the B field
• This force is always perpendicular to v
⇒ magnetic field never changes the speed (magnitude)
of a charge!
⇒ magnetic field never changes the kinetic energy of a
particle
⇒ magnetic field does no work!

11. Lorentz force
A charge feels both electric and magnetic forces.
r r r
r
F = q E +v × B
(
)
Lorentz force

12. In-class example: Lorentz force
A positive charge q with velocity v as shown enters a region with electric and
magnetic fields as in the figure (magnitudes are shown). What is the net
force on the charge? (Ignore gravity)
A. 0
B. −vB i + qE0 j
C. −vB k + qE0 j
D. vB i + qE0 j
−
−
−
−
−
y
v
E0
B0
z
+
+
+
+
+
E. qE0 j
B and v are antiparallel: vxB = 0
x

13. Circular motion in a uniform B field
Back to the Helmholtz demo:
• uniform B
• v is initially perpendicular to B
→ Uniform circular motion
F = qvB
v2
F = macentripetal = m
R
v2
qvB = m
R
R =
mv
qB

14. Helix
Now the initial velocity of the charges is NOT perfectly
perpendicular to B
F

15. Magnetic flux
How many magnetic field lines go through a given surface?
Line density is proportional to the magnitude of the magnetic field:
Φ = BAeffective
r r
A
= BA cos θ = B ×
For uniform B and
flat surfaces only
In general (for any field and surface):
r r
Φ = ∫B ×
da
Units : Weber
1 Wb = 1 Tm2
Convention: For closed surfaces, vector A points out.

16. Gauss’s law for magnetic fields
B-field lines are always continuous: no beginning or end.
For any closed surface,
# of lines entering the surface = # of lines leaving the surface
Φ closed surface
For E-fields: Φ closed surface
r r
=Ñ × =0
∫ B da
q
= enclosed
ε0
Electric charge
(“electric monopoles”)