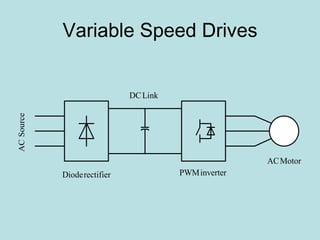
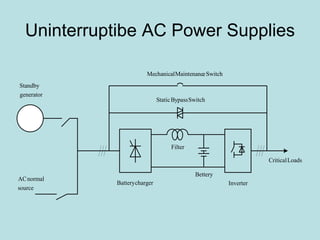
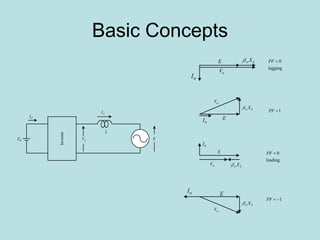
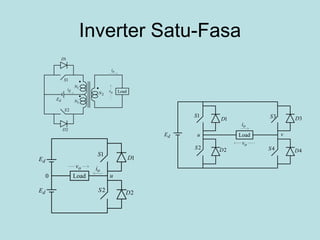
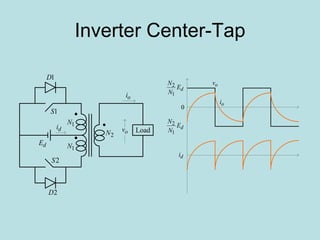
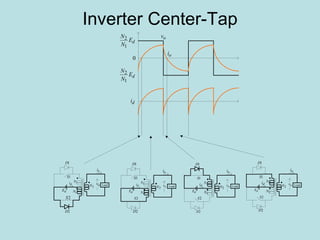
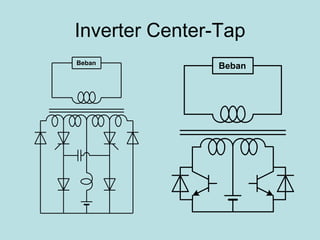
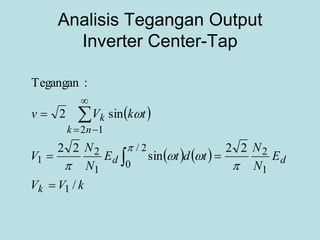
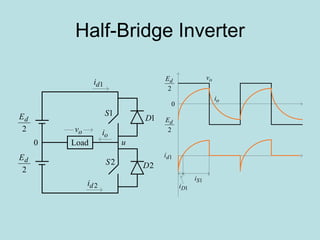
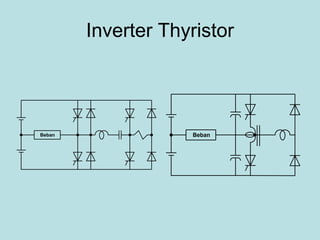
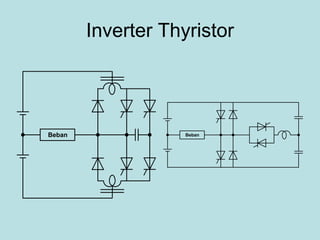
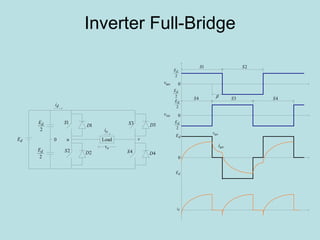
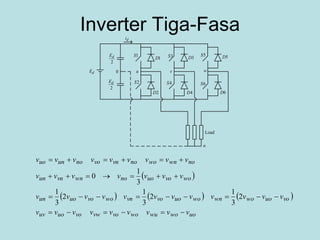
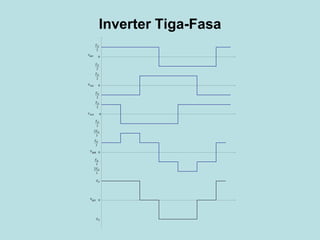
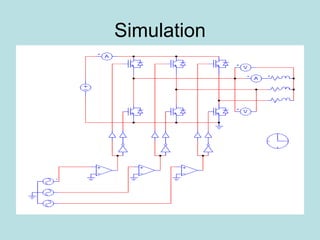
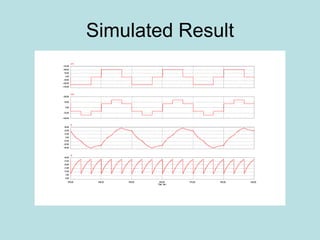
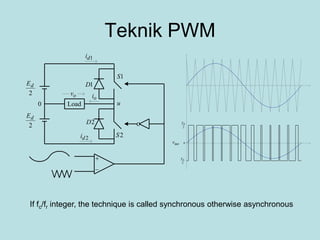
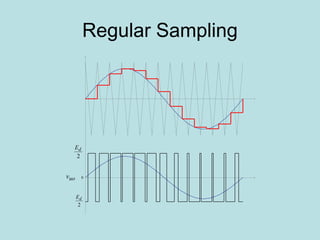
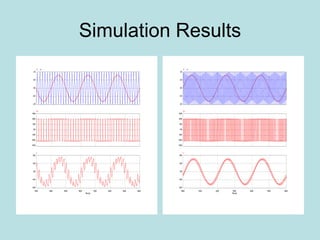
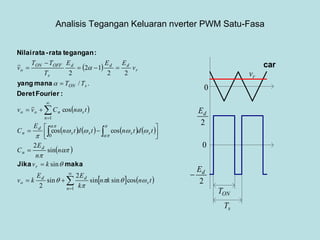
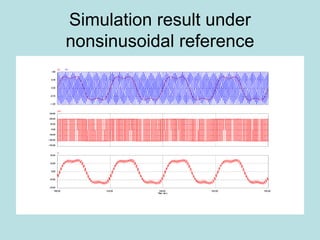
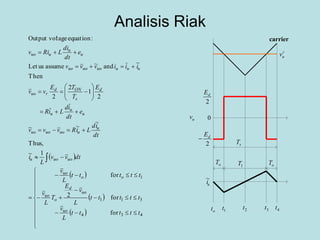
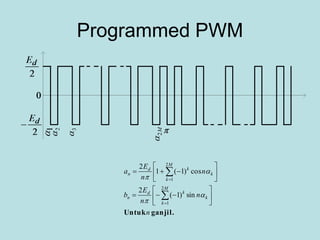
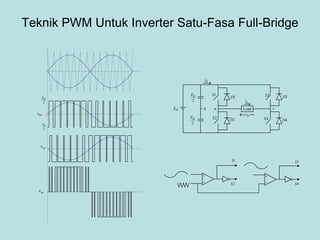
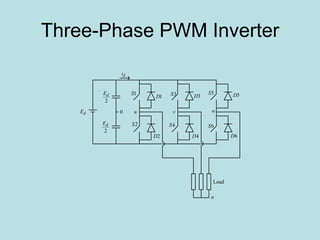
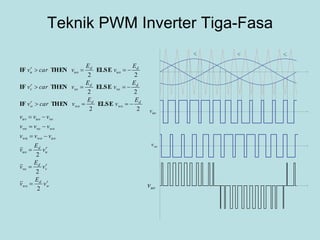
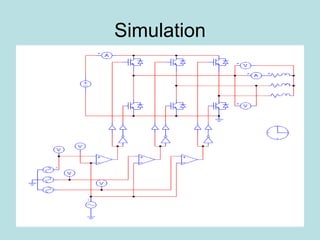
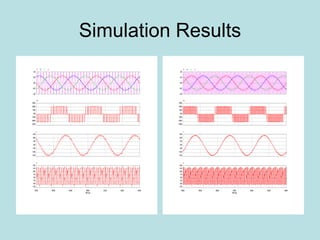
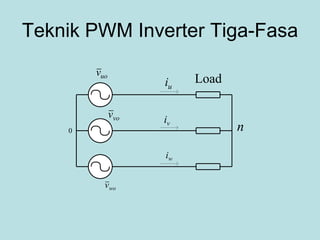
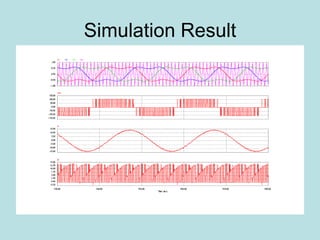
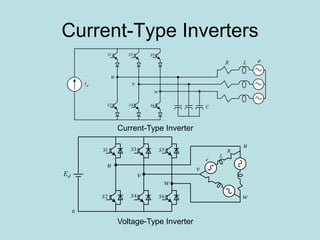
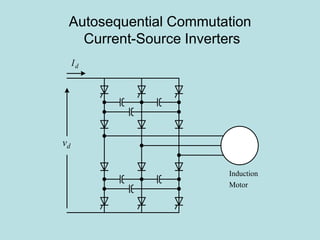
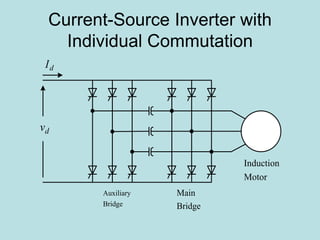
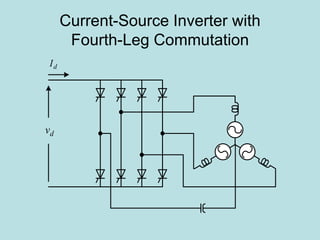
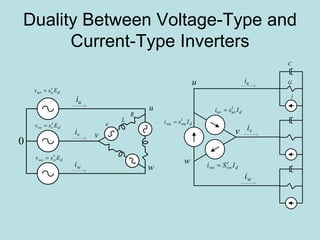
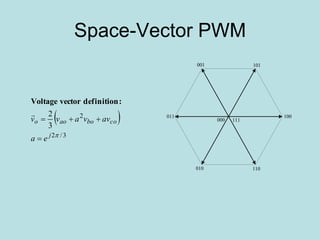
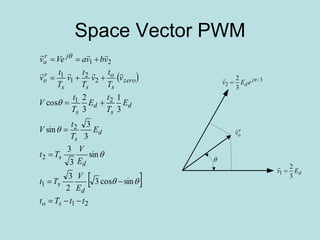
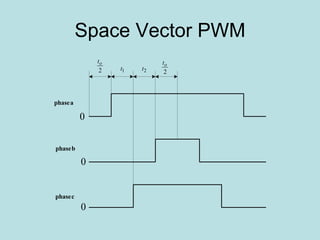
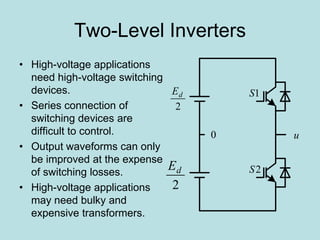
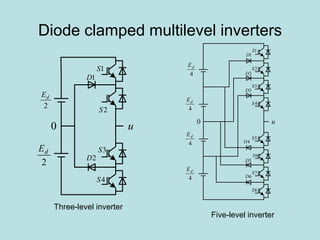
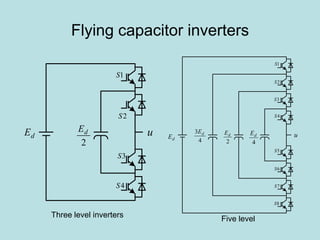
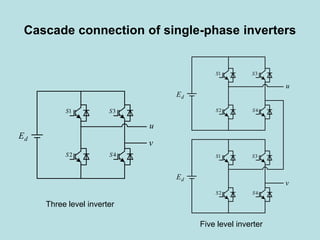
Inverter (Konverter DC – AC) are used for various applications such as AC motor control, UPS systems, active power filters, and flexible AC transmission systems. There are several types of inverters classified by number of phases, DC source, commutation method, output wave shaping technique, and number of output voltage levels. Basic inverter topologies include single phase, half bridge, full bridge, and three phase inverters. Pulse width modulation techniques are used to generate quasi-sinusoidal output voltage waveforms from the inverters. Simulation results show that higher switching frequencies produce more sinusoidal output currents.

1. Inverter (Konverter DC – AC)
Pekik Argo Dahono

2. Penggunaan Inverter
• Pengendalian motor ac
• UPS
• Catu daya ac
• Ballast elektronik
• Microwave heating
• Static VAR generators
• FACTS (Flexible AC Transmission System)
• Filter daya aktif
• Penyearah

3. Variable Speed Drives
SourceAC
rectifierDiode inverterPWM
LinkDC
MotorAC

4. Uninterruptibe AC Power Supplies
chargerBattery
Bettery
Inverter
Filter
SwitchBypassStatic
SwitcheMaintenancMechanical
LoadsCritical
source
normalAC
generator
Standby

5. Basic Concepts
oV E
L
oI
dE
dI
Inverter
oV
Lo XjI
E
E
E
Lo XjI
Lo XjI
oV
oV
E Lo XjI
oV
lagging
0PF
1PF
leading
0PF
1PF
oI
oI
oI
oI

6. Properties of Ideal Inverters
• DC input is free of ripple
• AC output is sinusoidal or has a
controllable waveshape

7. Klasifikasi Inverter
1) Menurut jumlah fasa
- satu-fasa
- banyak fasa
2) Menurut sumber dc:
- sumber tegangan
- sumber arus
3) Menurut metoda komutasi:
- komutasi paksa
- komutasi natural
4) Menurut metoda pengaturan gelombang ac:
- gelombang persegi
- pulse amplitude modulation (PAM)
- pulse width modulation (PWM)
5) Menurut jumlah level gelombang keluaran:
- dua level
- banyak level

8. Inverter Satu-Fasa
dE


1S
1D
2S
2D
ov Load
oi
1N
1N
2N
di
dE
1S
1D
2S 2D
dE
Load u0
ov
oi
dE
1S
1D
2S 2D
Load
3S 3D
4S 4D
u v
ov
oi

9. Inverter Center-Tap
dE


1S
1D
2S
2D
ov Load
oi
1N
1N
2N
di
dE
N
N
1
2
dE
N
N
1
2
0
ov
oi
di

10. Inverter Center-Tap
dE
N
N
1
2
dE
N
N
1
2
0
ov
oi
di
dE


1S
1D
2S
2D
ov Load
oi
1N
1N
2Ndi
dE


1S
1D
2S
2D
ov Load
oi
1N
1N
2Ndi
dE


1S
1D
2S
2D
ov Load
oi
1N
1N
2Ndi
dE


1S
1D
2S
2D
ov Load
oi
1N
1N
2Ndi

11. Inverter Center-Tap
BebanBeban

12. Analisis Tegangan Output
Inverter Center-Tap
 
   
kVV
E
N
N
tdtE
N
N
V
tkVv
k
dd
nk
k
/
22
sin
22
sin2
:Tegangan
1
1
22/
0
1
2
1
12













13. Inverter Center-Tap
• Sederhana
• Komponen minimum
• Harus pakai trafo
• Cocok untuk daya rendah (< 1 kW)
• Cocok untuk tegangan dc yang rendah
• Pengaturan tegangan dilakukan dengan
menggunakan trafo ferroresonance.

14. Half-Bridge Inverter
1S
1D
2S 2D
2
dE
Load u0
ov
oi
2
dE
1di
2di
2
dE
0
ov
oi
2
dE
1Si
1Di
1di

15. Analisis Tegangan Output
Inverter Half-Bridge
 
   
kVV
Etdt
E
V
tkVv
k
d
d
nk
ko
/
2
sin
2
sin2
:Tegangan
1
2/
01
12













16. Inverter Thyristor
Beban Beban

17. Inverter Thyristor
Beban Beban

18. Inverter Full-Bridge
2
dE
2
dE
0
2
dE
2
dE
0
0
dE
dE
uov
vov
uvv
uvi

1S 2S
4S 3S 4S
di
1S
1D
2S 2D
Load
3S 3D
4S 4D
u v
ov
oi
dE
2
dE
2
dE
0
di

19. Inverter Full-Bridge
 
     
 
 
 
 2/7cos
7
22
2/5cos
5
22
2/3cos
3
22
2/cos
22
2/cos
22
sin
22
sin2
7
5
3
1
2/
2/
12















d
d
d
d
ddk
nk
ko
EV
EV
EV
EV
kE
k
tdtkEV
tkVv











20. Inverter Tiga-Fasa
 
     
uowowuwovovwvououv
vouowownwouovovnwovououn
wovouonownvnun
nownwonovnvonounuo
vvvvvvvvv
vvvvvvvvvvvv
vvvvvvv
vvvvvvvvv




2
3
1
2
3
1
2
3
1
3
1
0
1S
1D
2S
2D
udE
2
dE
2
dE
0
di
3S 3D
4S
4D
v
5S 5D
6S
6D
w
n
Load

21. Inverter Tiga-Fasa
2
dE
2
dE
0
0
0
0
0
2
dE
2
dE
2
dE
2
dE
3
2 dE
3
dE
3
dE
3
2 dE
dE
dE
uov
vov
wov
unv
uvv

22. Inverter Tiga-Fasa
 
 
dll
nk
nk
kphun
phkph
dph
nk
kphuo
EV
tkVv
kVV
EV
tkVv




6
:fasaantarTegangan
sin2
netral-ke-fasaTegangan
/
2
sin2
nol-ke-fasaTegangan
1,
3
12
,
1,,
1,
12
,













23. Simulation

24. Simulated Result

25. Teknik PWM
1. Sampling Based PWM:
• Natural sampling (Carrier Based)
• Regular sampling
2. Programmed PWM:
• Eliminated Harmonics
• Minimum Harmonics

26. Teknik PWM
1S
2
dE
Load0
ov
oi
2
dE
1di
2di
1D
2S
2D
u


o 2
dE
0
2
dE
uov
If fc/fr integer, the technique is called synchronous otherwise asynchronous

27. Regular Sampling
2
dE
0
2
dE
uov

28. Simulation

29. Simulation Results

30. Analisis Tegangan Keluaran nverter PWM Satu-Fasa
 
 
       
 
   












 





1
0
1
cossinsin
2
sin
2
sin
sin
2
coscos
cos
./
22
12
2
n
s
dd
o
r
d
n
ssss
d
n
n
snoo
sON
r
ddd
s
OFFON
o
tnkn
k
EE
kv
kv
n
n
E
C
tdtntdtn
E
C
tnCvv
TT
v
EEE
T
TT
v














makaJika
:FourierDeret
manayang
:teganganrata-rataNilai
0
0
2
dE
2
dE

rv
car
ONT
sT

31. Simulation result under
nonsinusoidal reference

32. Analisis Tegangan keluaran
• Maximum peak output voltage is Ed/2. This
value is less than the fundamental
component of square-wave output voltage.
• The output current waveform is almost
sinusoidal when the switching frequency is
high.
• Because the switching frequency is high,
the switching losses are also high.

33. Analisis Riak
0
2
dE

2
dE
r
uv
carrier
ot 1t 2t 3t 4t
sT
1ToT oT
ui
~
uv
 
 
 
 






























434
311
1
for
for2
for
1~
Thus,
~
~~
2
1
2
2
Then
~
and~assumeusLet
:equationtageOutput vol
ttttt
L
v
ttttt
L
v
E
T
L
v
ttttt
L
v
dtvv
L
i
dt
id
LiRvvv
e
dt
id
LiR
E
T
TE
vv
iiivvv
e
dt
di
LRiv
uo
uo
d
o
uo
oo
uo
uouou
u
uuououo
u
u
u
d
s
ONd
ruo
uuuuououo
u
u
uuo

34. Analisis Riak












2
0
2
,
22
1
~
2
1~
~1~
sin
2
1
2
1
2
1
2
12
dII
dti
T
I
kv
v
T
T
v
T
T
uavu
Tt
t u
s
u
r
u
r
s
r
u
s
o
so
o
:rippleofvalueRMS
:rippleofvaluesquareMean

35. Programmed PWM
ganjil.Untukn
n
n
E
b
n
n
E
a
M
k
k
kd
n
M
k
k
kd
n


















2
1
2
1
sin)1(
2
cos)1(1
2





36. Teknik PWM Untuk Inverter Satu-Fasa Full-Bridge
2
dE
2
dE
uov
vov
uvv
1S
1D
2S 2D
Load
3S 3D
4S 4D
u v
ov
oi
dE
2
dE
2
dE
0
di


o


o
1S
2S
3S
4S

37. Three-Phase PWM Inverter
1S
1D
2S
2D
udE
2
dE
2
dE
0
di
3S 3D
4S
4D
v
5S 5D
6S
6D
w
n
Load

38. Teknik PWM Inverter Tiga-Fasa
r
uv r
vv r
wv
uov
vov
uvv
r
w
d
wo
r
v
d
vo
r
u
d
uo
uowowu
wovovw
vououv
d
wo
d
wo
r
w
d
vo
d
vo
r
v
d
uo
d
uo
r
u
v
E
v
v
E
v
v
E
v
vvv
vvv
vvv
E
v
E
vcarv
E
v
E
vcarv
E
v
E
vcarv
2
2
2
22
22
22









ELSETHENIF
ELSETHENIF
ELSETHENIF

39. Simulation

40. Simulation Results

41. Teknik PWM Inverter Tiga-Fasa
n
Load
0
uov
vov
wov
wi
vi
ui

42. Teknik PWM Inverter Tiga-Fasa
 
 
PWMvectorSpace-
PWMousDiscontinu
-
:popularmostThe













3sin
4
3sin
6
sin
sin
sin
3
2
3
2
k
s
k
s
skv
skv
skv
o
o
o
r
w
o
r
v
o
r
u

43. Simulation Result

44. Switching Function Concept
 
 
 
functionswitchingphase-to-phaseis
ELSETHENIF
ELSETHENIF
ELSETHENIF
otherwisethen
signalONanreceivesdeviceswitchinguppertheIF
uv
dwuduwuGwGwu
dvwdwvwGvGvw
duvdvuvGuGuv
dwwGdvvGduuG
ww
r
w
vv
r
v
uu
r
u
s
EsEssvvv
EsEssvvv
EsEssvvv
EsvEsvEsv
sscarv
sscarv
sscarv
ss








01
01
01
.01

45. Current-Type Inverters
R L e
C
1S
u
2S
3S
v
4S 6S
w
5S
dI
0
u
1S
2S
u
v
w
R
L
e
3S
v
4S
5S
6S
w
dE
Current-Type Inverter
Voltage-Type Inverter

46. Autosequential Commutation
Current-Source Inverters
Motor
Induction
dI
dv

47. Current-Source Inverter with
Individual Commutation
dI
dv
Bridge
Auxiliary
Bridge
Main
Motor
Induction

48. Current-Source Inverter with
Fourth-Leg Commutation
dI
dv

49. Duality Between Voltage-Type and
Current-Type Inverters
0
d
v
uuo Esv 
d
v
vvo Esv 
d
v
wwo Esv 
ui
vi
wi
u
v
w
R
L
e
u
v
w
C
G
j
d
i
uvuv Isi 
d
i
vwvw ISi 
d
i
wuwu Isi 
ui
vi
wi

50. Duality Between Voltage-Type and
Current-Type Inverters
r
uvi r
vwi r
wui
0
1
i
uvs
0
1
1
i
vs
i
vws 0
1
r
uv r
vv r
wv
0
1
v
us
0
1
1
v
uvs
v
vs
0
1

51. Current-Type Inverters
.continuitycurrentsorceensuretodevices
switchinglowerandupperofpaironeON-turnthenzeroareandallIF
signal.ONanreceivesS6norS5neitherIFand
signal,ONanreceivesS6THENIFsignal,ONanreceivesS5THENIF
signal.ONanreceivesS4norS3neitherIFand
signal,ONanreceivesS4THENIFsignal,ONanreceivesS3THENIF
signal.ONanreceivesS2norS1neitherIFand
signal,ONanreceivesS2THENIFsignal,ONanreceivesS1THENIF
ELSETHENIF
ELSETHENIF
ELSETHENIF
i
w
i
v
i
u
i
w
i
w
i
w
i
v
i
v
i
v
i
u
i
u
i
u
i
wu
i
vw
i
w
i
vw
i
uv
i
v
i
uv
i
wu
i
u
i
wu
i
wu
r
wu
i
vw
i
vw
r
vw
i
uv
i
uv
r
uv
sss
s
ss
s
ss
s
ss
sssssssss
sscari
sscari
sscari
,,
0
11
0
11
0
11
01
01
01











52. Current-Type Inverters
• At present, voltage-type inverters are more popular than
current-type inverters.
• Current-type inverters are commonly used as PWM
rectifiers.
• Advances on superconductor will increase the use of
current-type inverters.
• At present, several manufacturers introduce reverse-
blocking devices on one module.
• Current-type inverters are introduced for medium voltage
ac drives because the input and output currents are
almost sinusoidal, inherently four-quadrants, and short-
circuit proof.

53. Space-Vector PWM
 
3/2
2
3
2
j
coboaoo
ea
avvavv



:definitionvectorVoltage
100011
101001
010 110
111000

54. Space Vector PWM
 
 
21
1
2
2
21
2
2
1
1
21
sincos3
2
3
sin
3
3
3
3
sin
3
1
3
2
cos
ttTt
E
V
Tt
E
V
Tt
E
T
t
V
E
T
t
E
T
t
V
v
T
t
v
T
t
v
T
t
v
vbvaVev
so
d
s
d
s
d
s
d
s
d
s
zero
s
o
ss
r
o
jr
o














dEv
3
2
1 

3/
2
3
2 j
deEv 

r
ov



55. Space Vector PWM
aphase
bphase
cphase
2
ot
1t 2t 2
ot
0
0
0

56. Two-Level Inverters
• High-voltage applications
need high-voltage switching
devices.
• Series connection of
switching devices are
difficult to control.
• Output waveforms can only
be improved at the expense
of switching losses.
• High-voltage applications
may need bulky and
expensive transformers.
2
dE
2
dE
u0
1S
2S

57. Diode clamped multilevel inverters
2
dE
2
dE
u0
1S
2S
1D
2D
3S
4S
0
1D
u
1S
2S
3S
4S
4
dE
2D
3D
4D
5D
6D
5S
6S
7S
8S
4
dE
4
dE
4
dE
Three-level inverter
Five-level inverter

58. Flying capacitor inverters
2
dE u
1S
2S
3S
4S
dE
Three level inverters Five level
2
dE u
1S
2S
3S
4S
dE
4
3 dE
4
dE
5S
6S
7S
8S

59. Cascade connection of single-phase inverters
u
1S
2S
v
3S
4S
dE
1S
2S
v
3S
4S
dE
u
1S
2S
3S
4S
dE
Three level inverter
Five level inverter