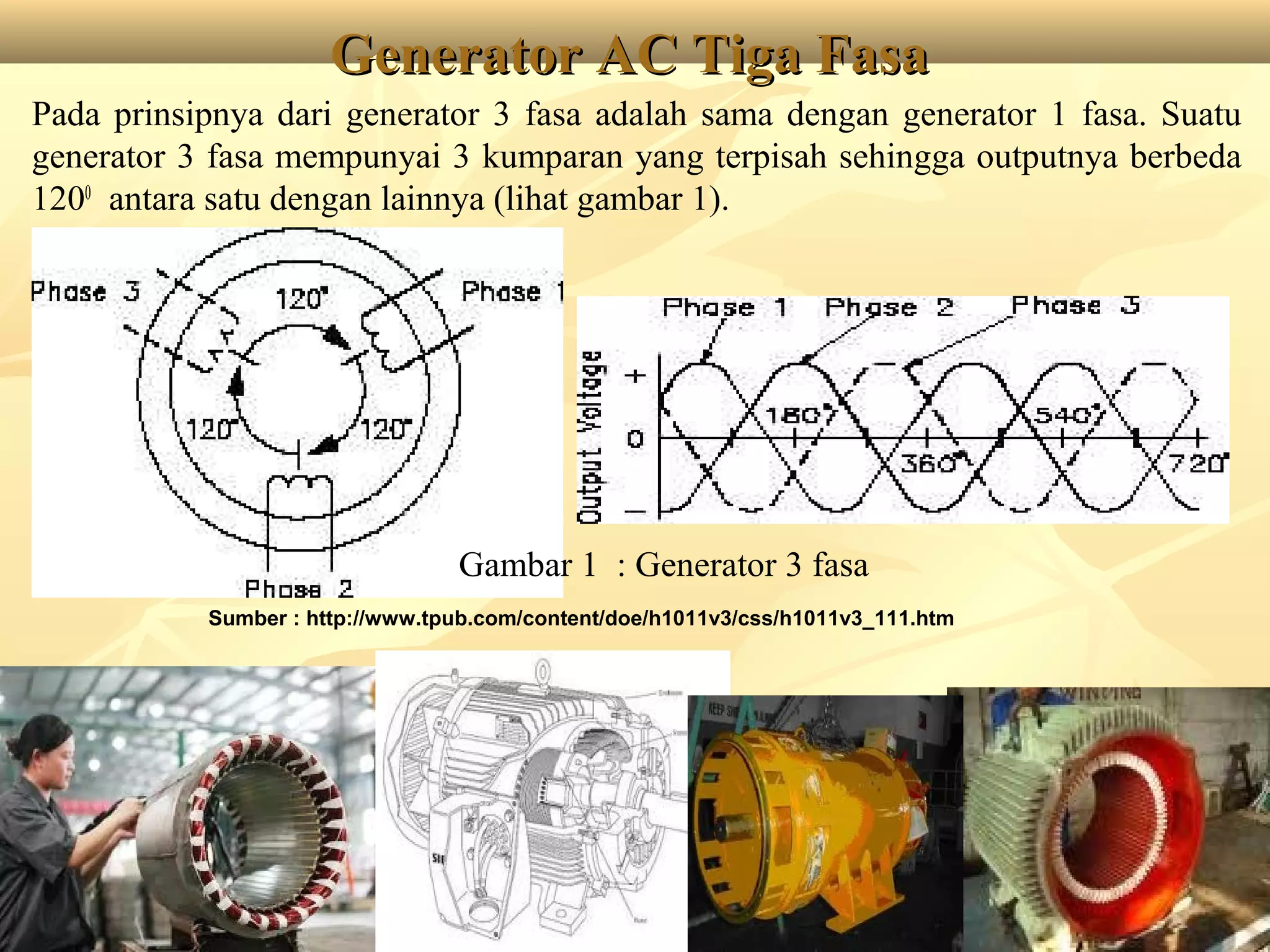
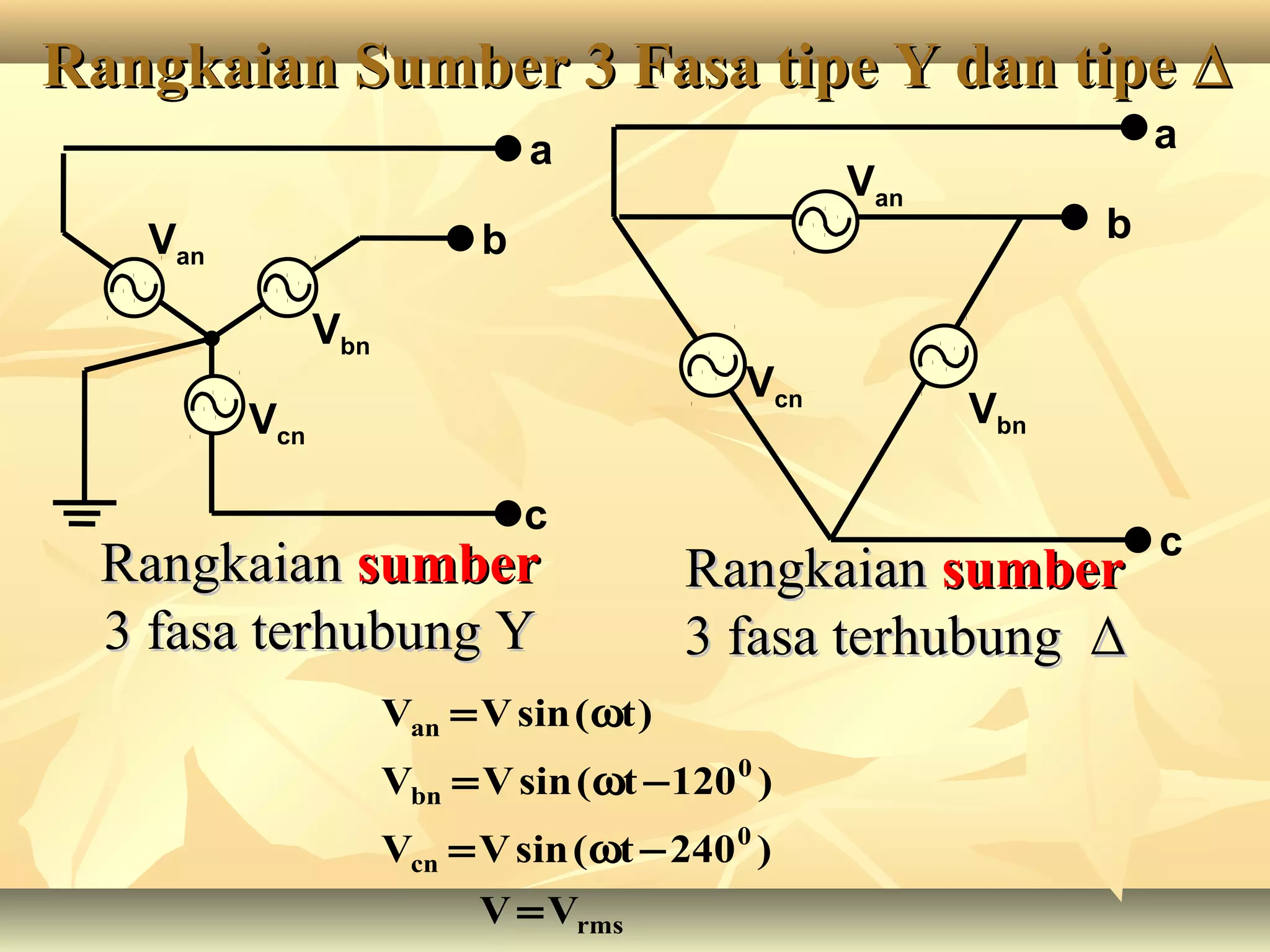
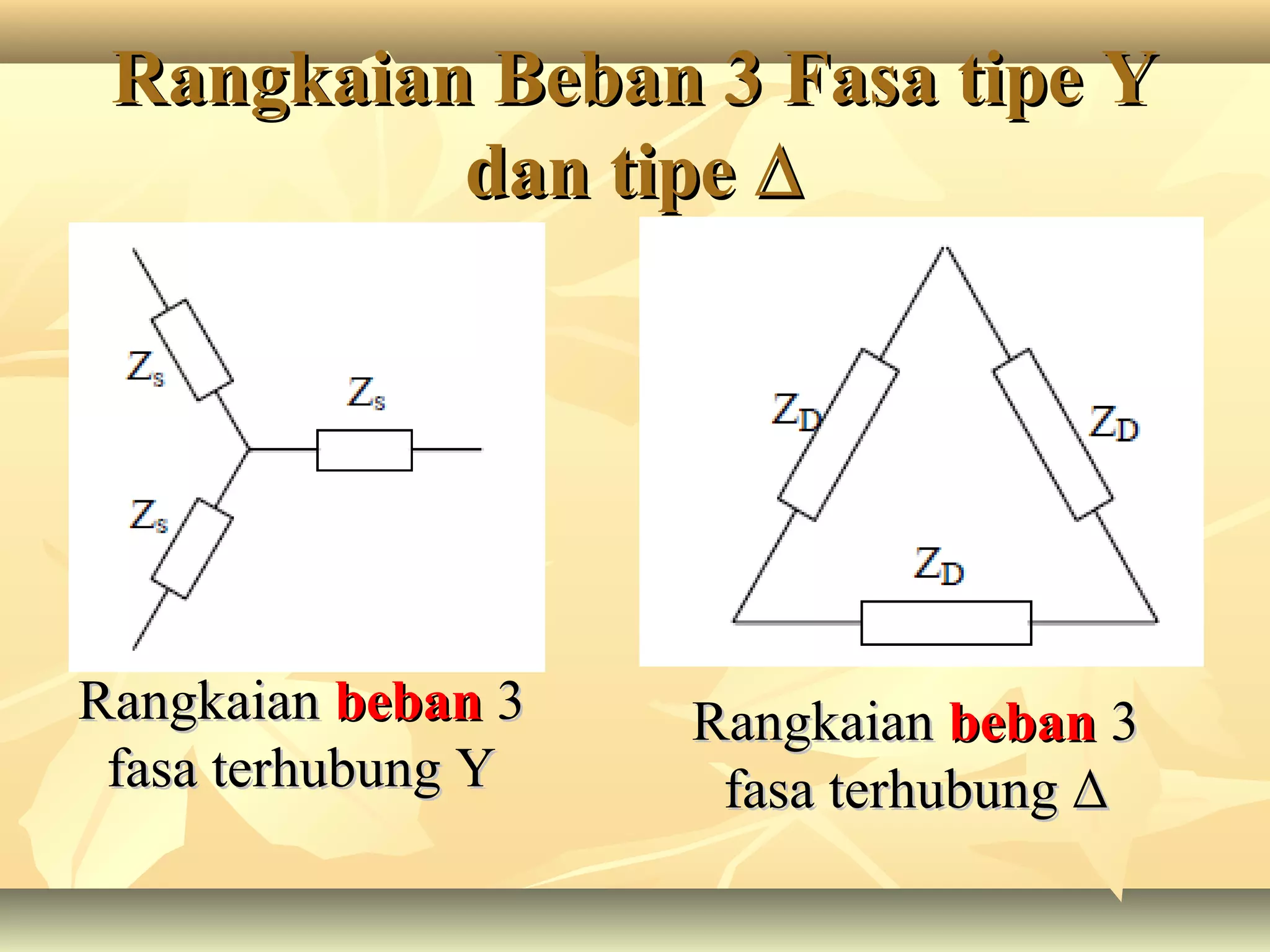
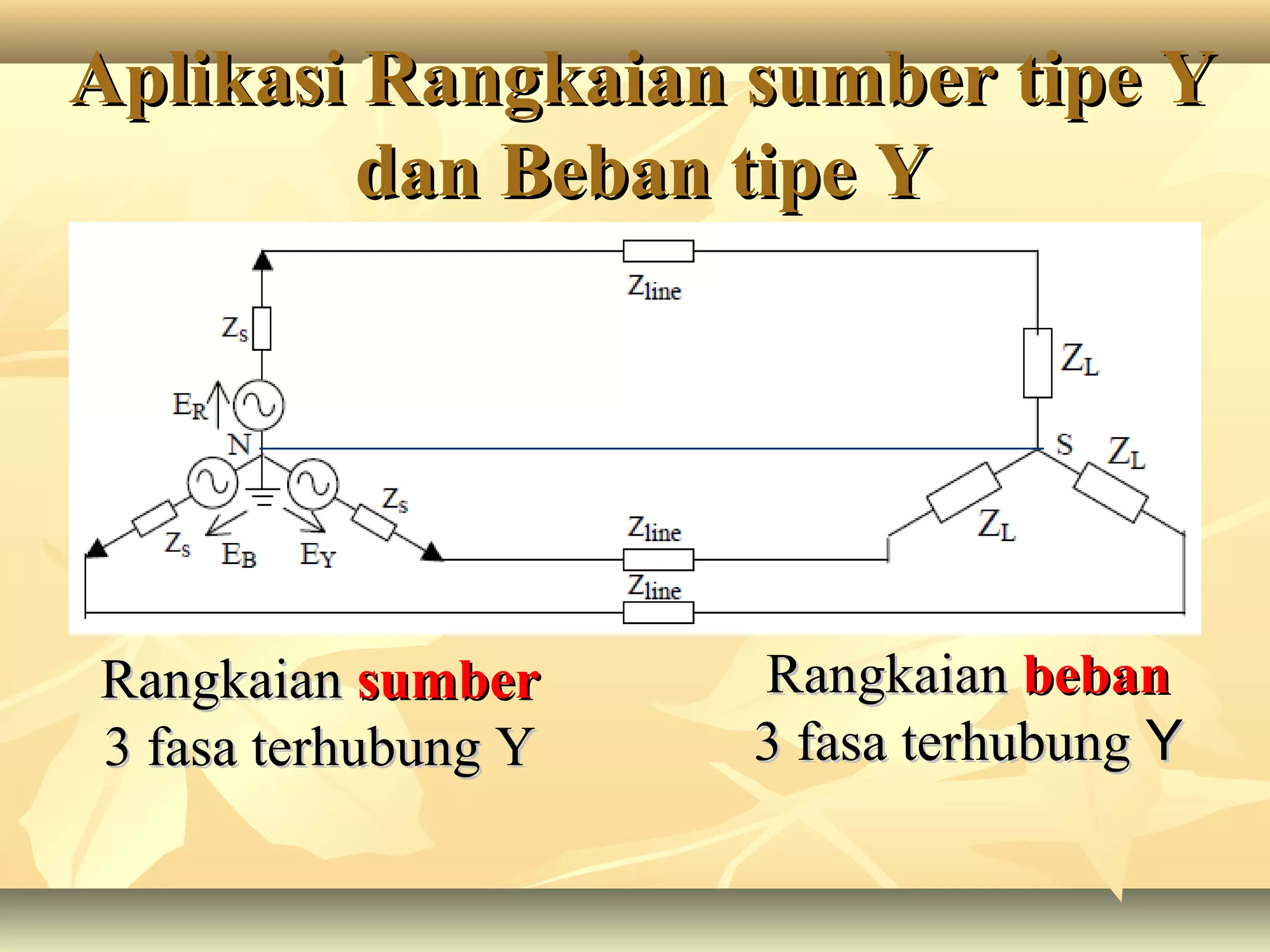
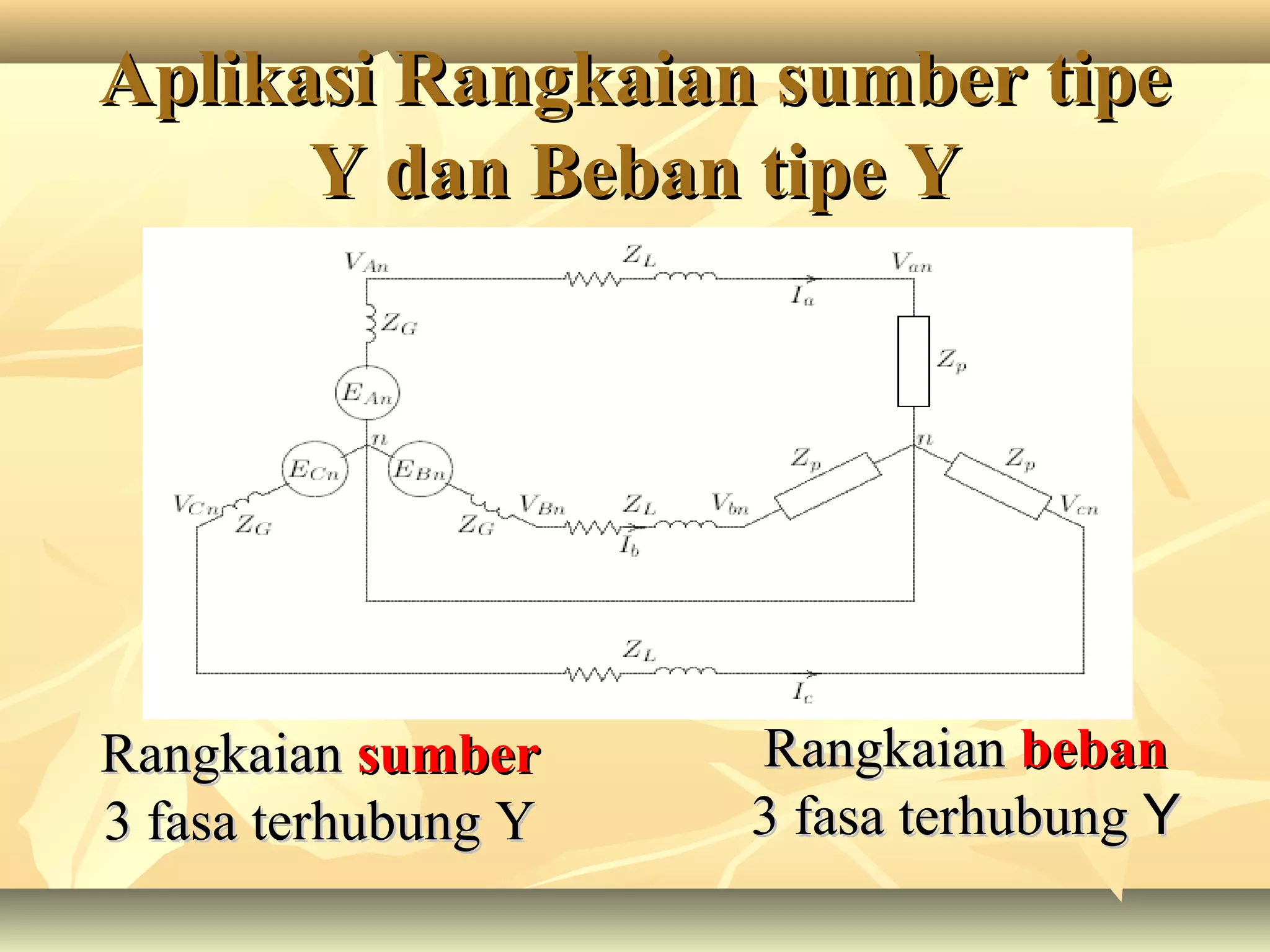
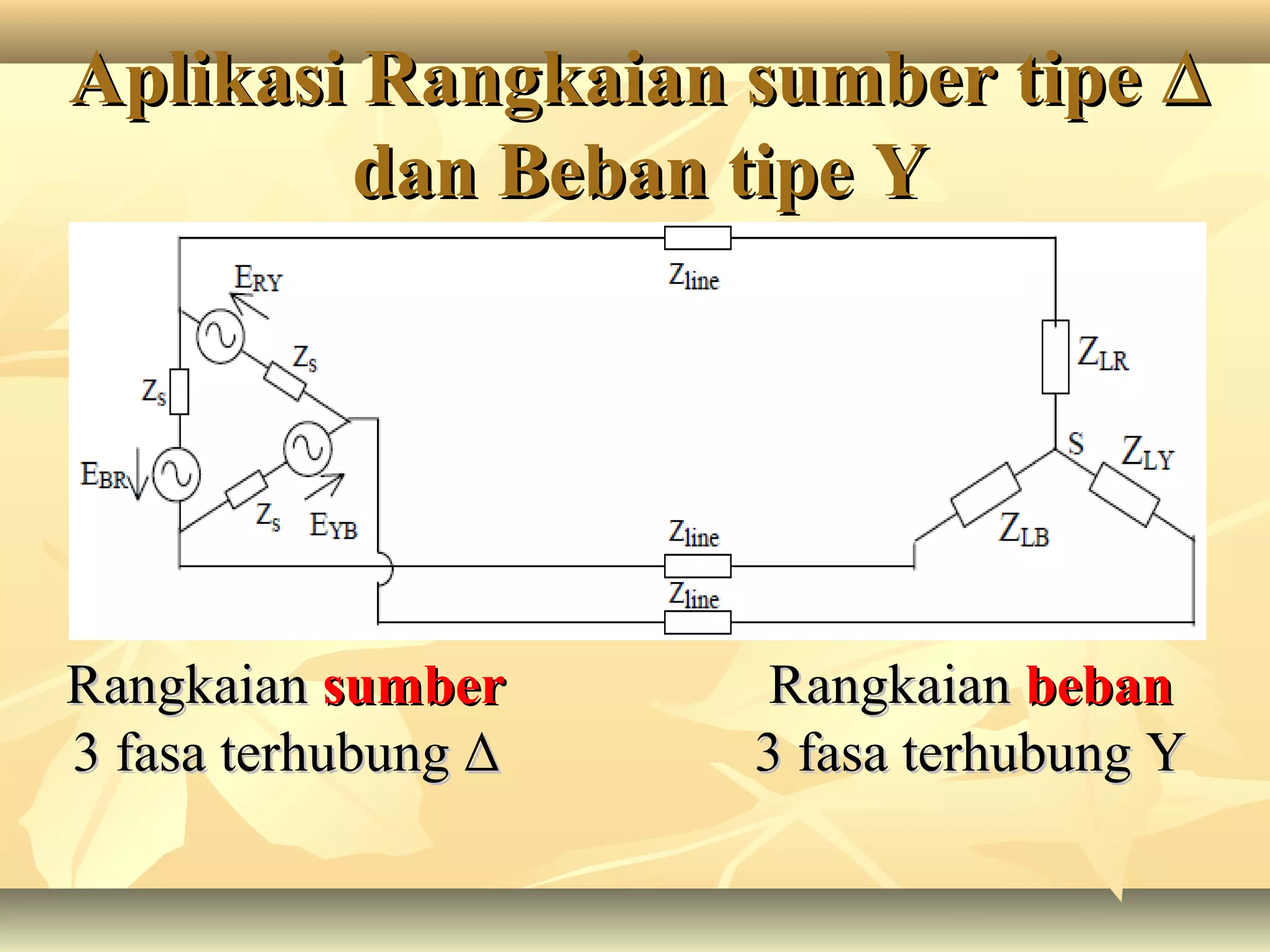
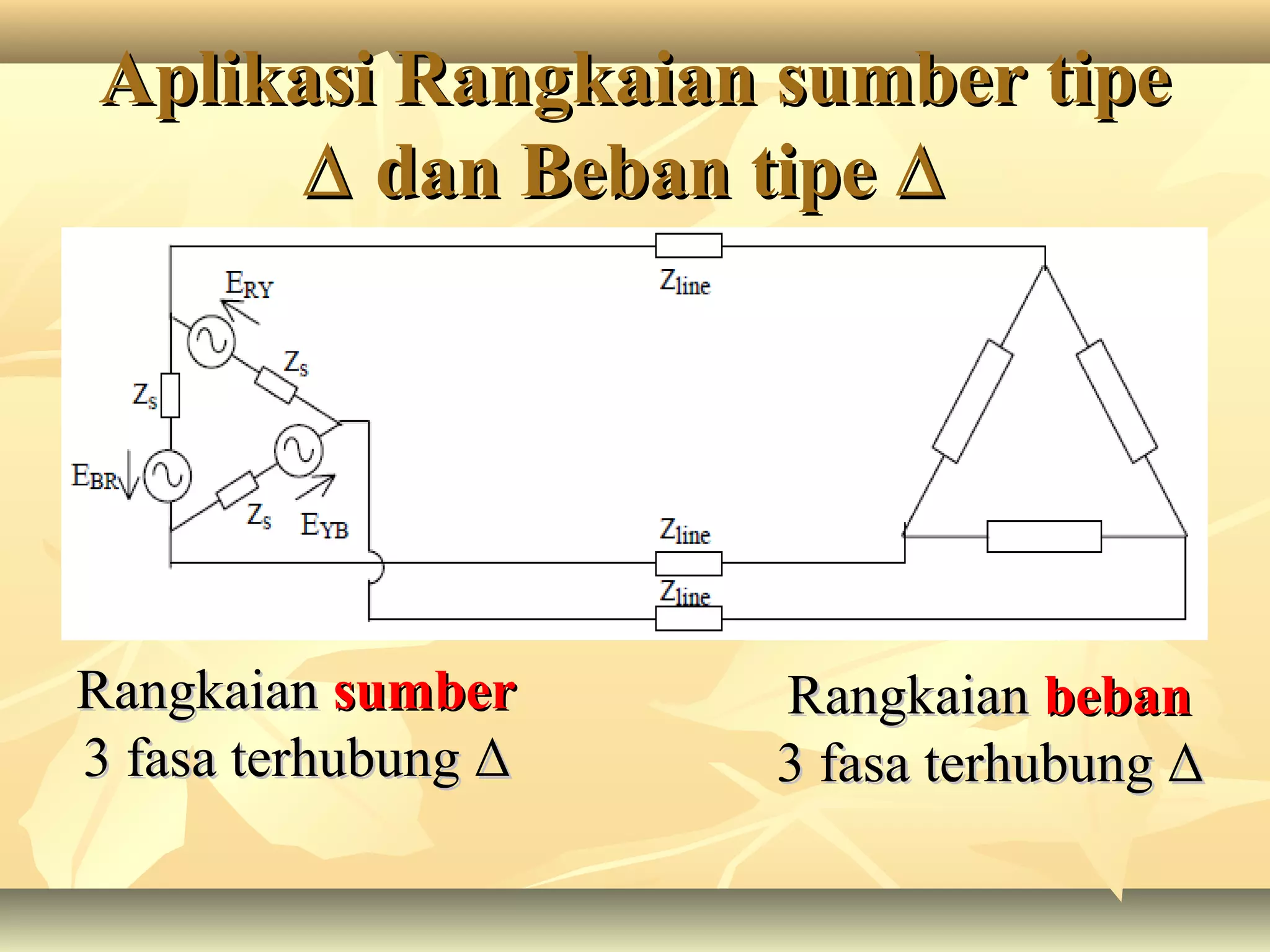
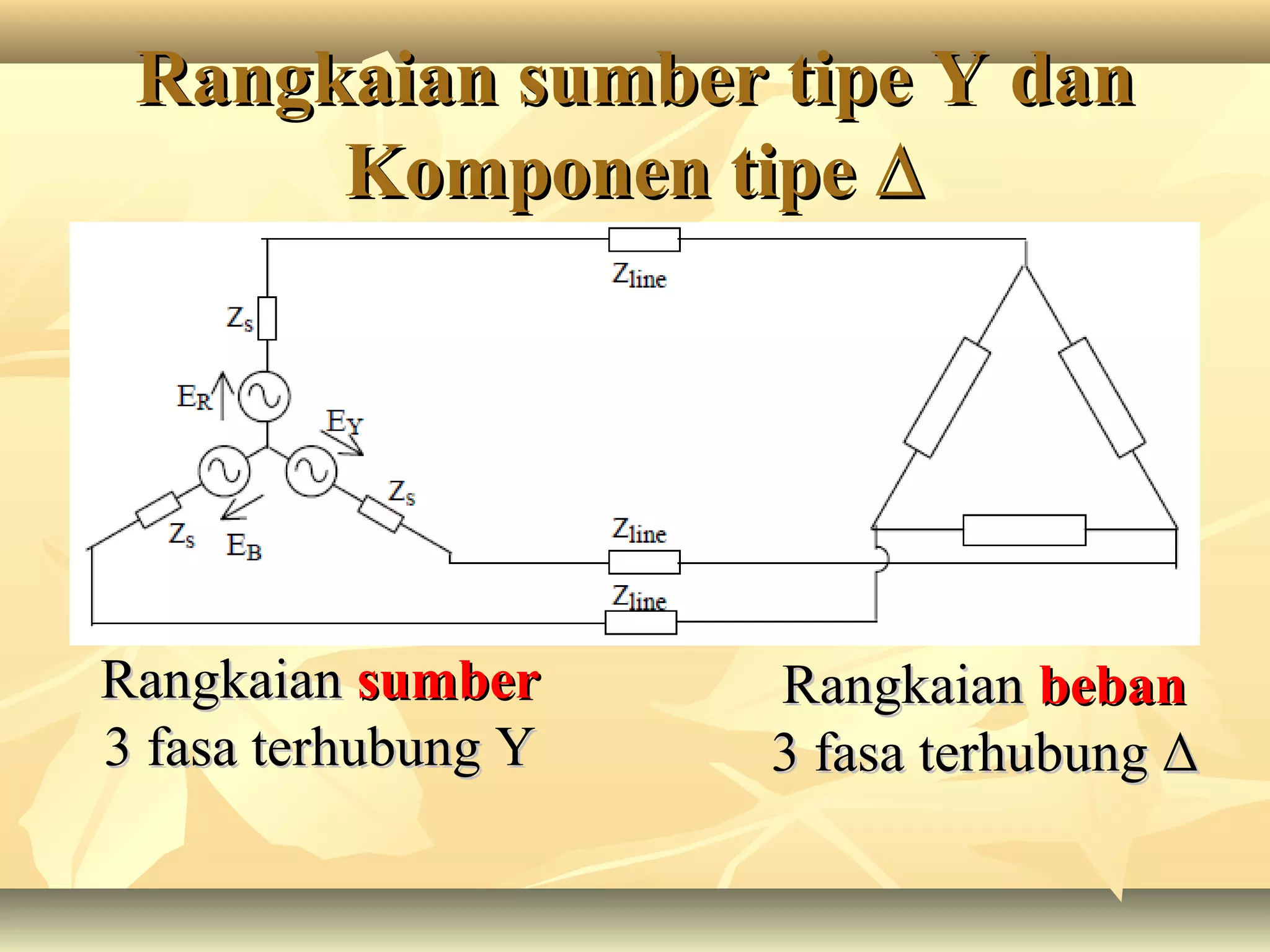
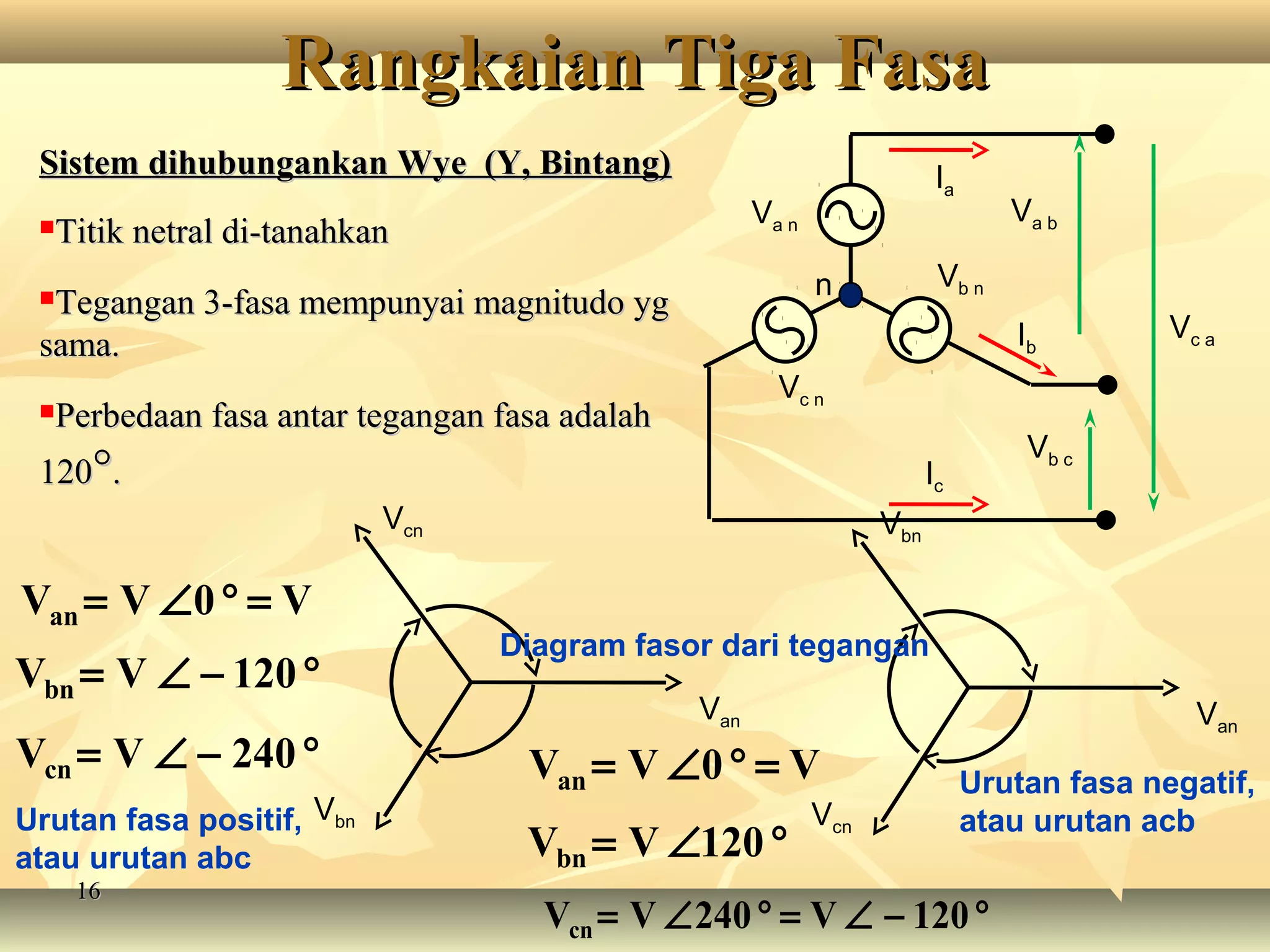
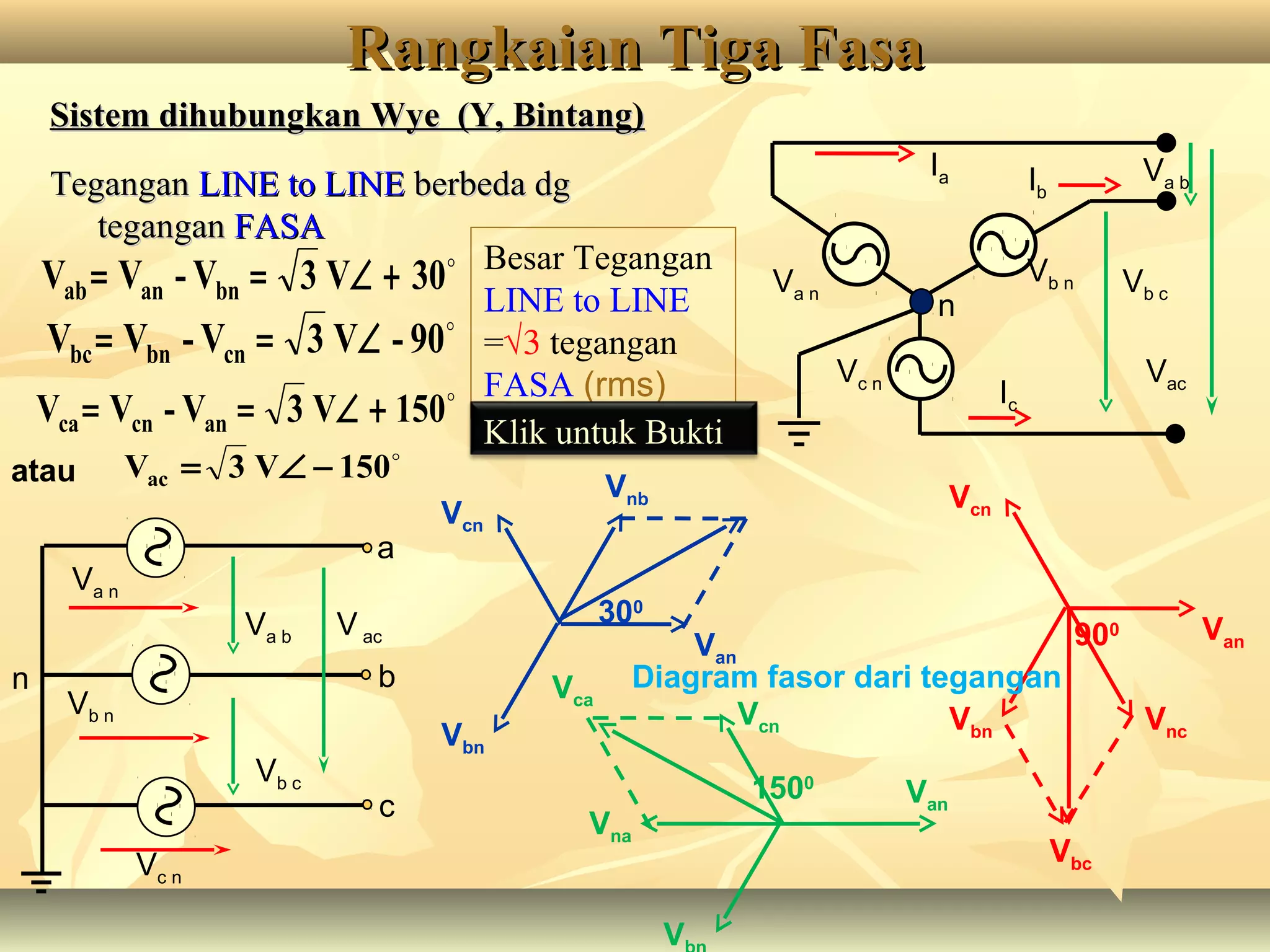
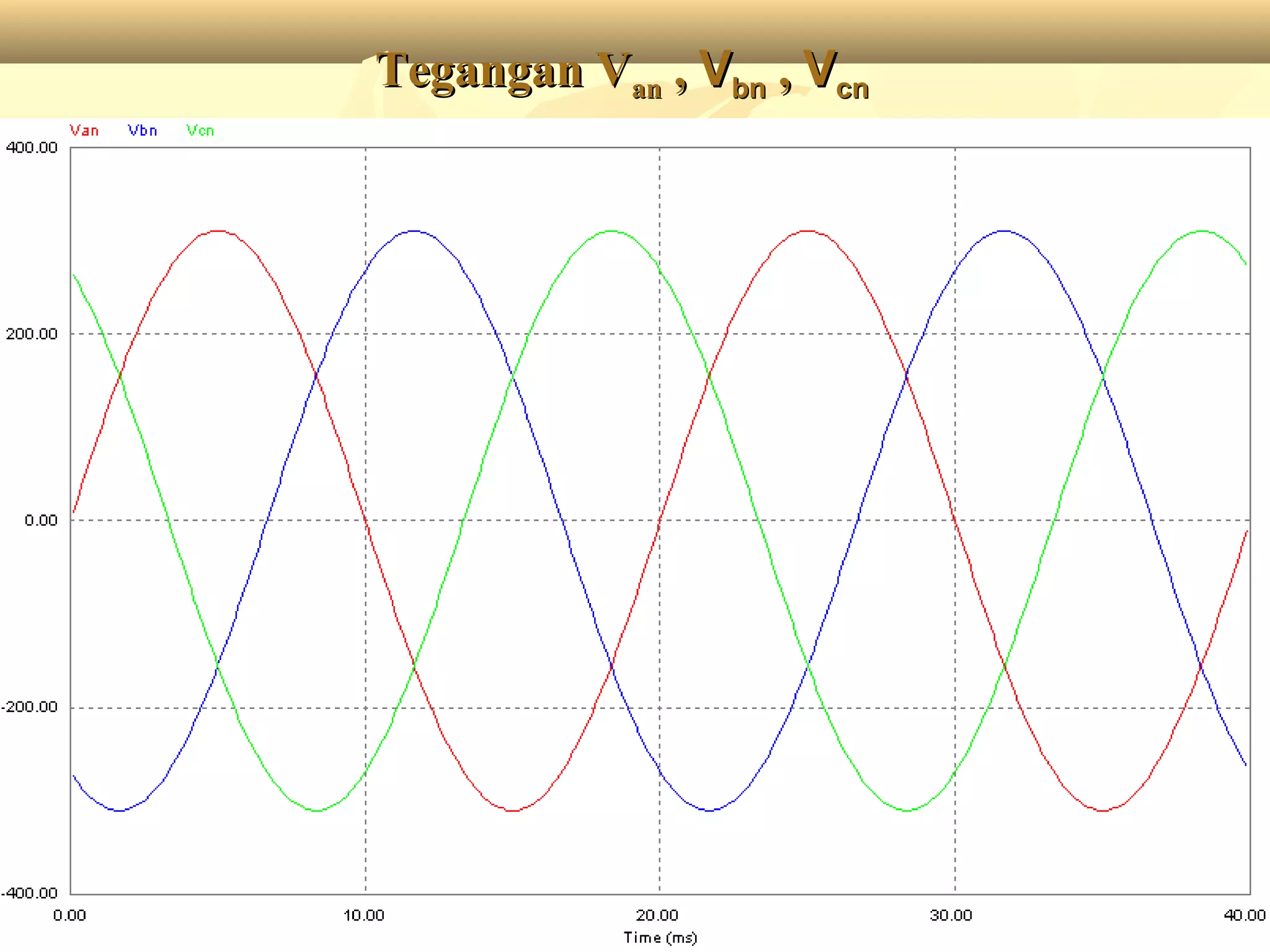
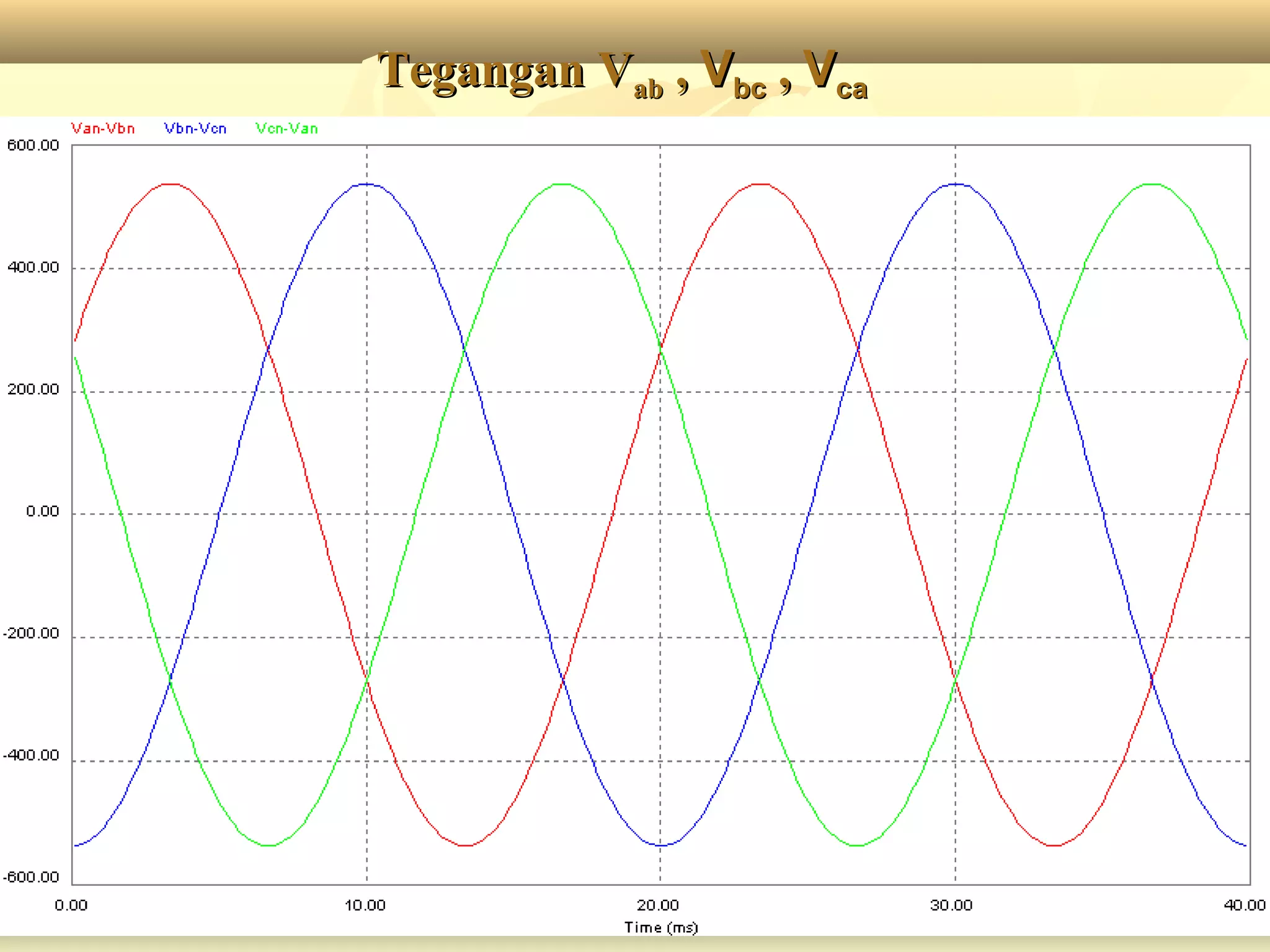
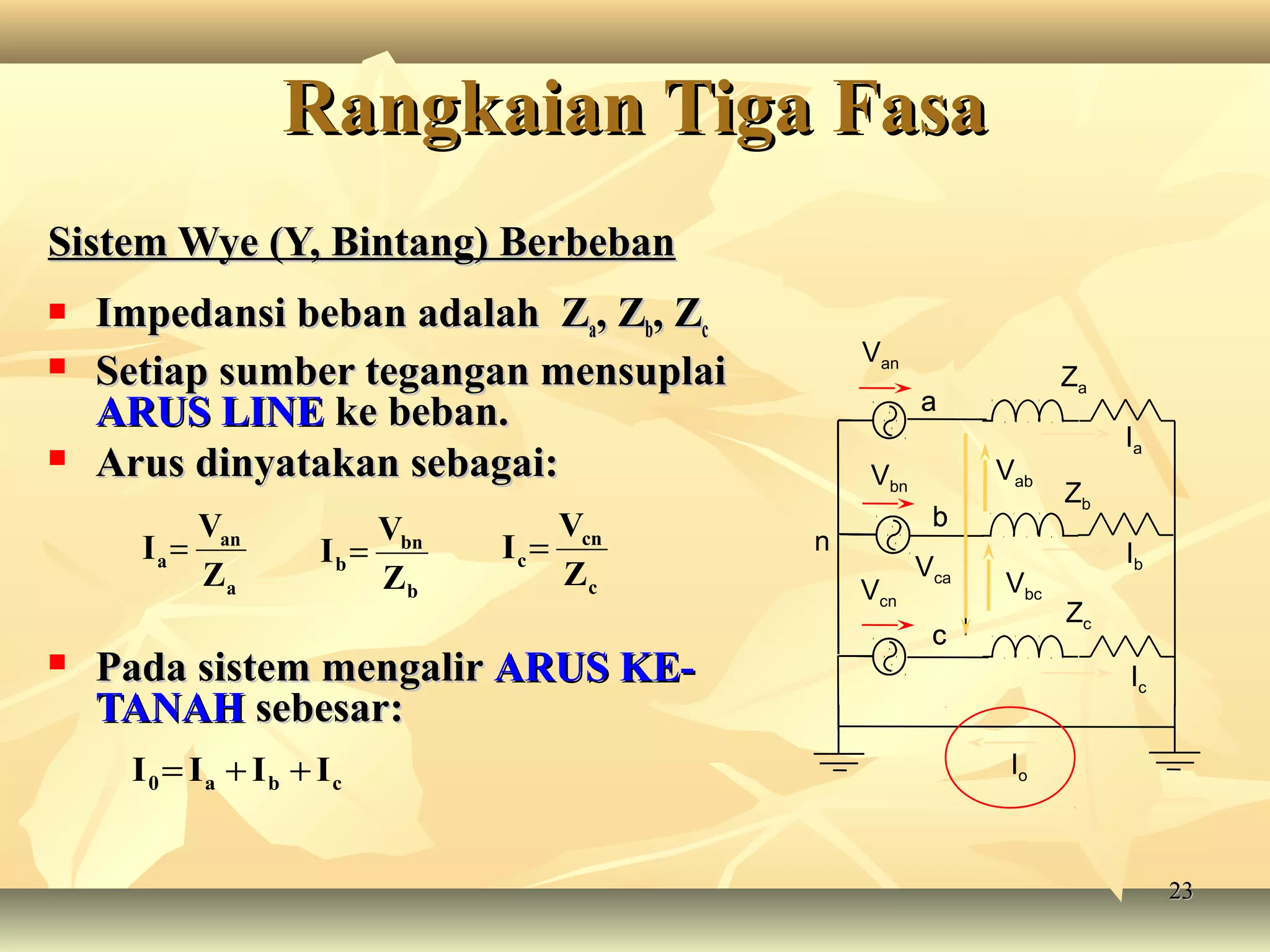
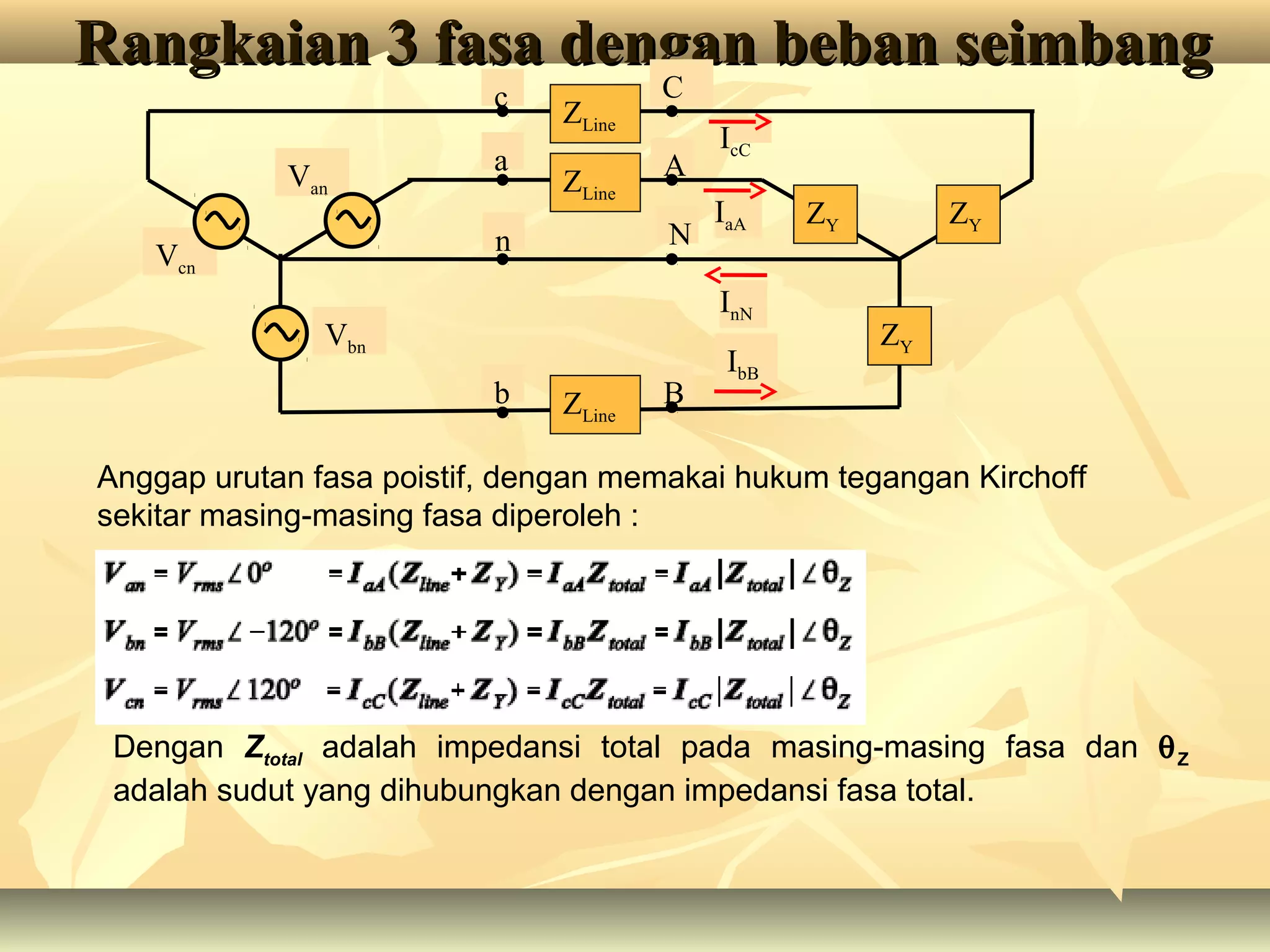
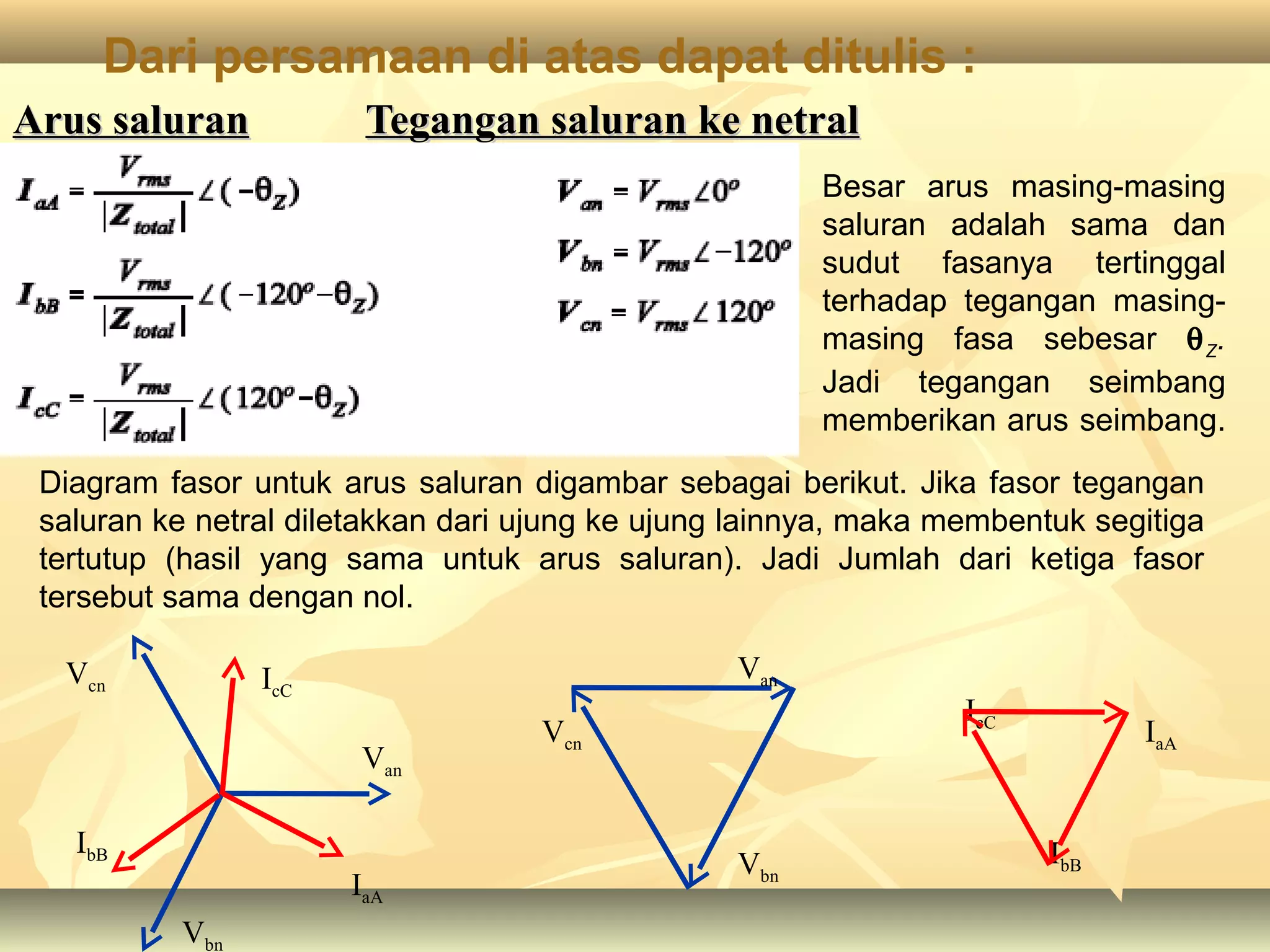
Dokumen tersebut membahas tentang rangkaian listrik tiga fasa, mulai dari penjelasan tentang generator tiga fasa, rangkaian sumber tiga fasa tipe Y dan Δ, rangkaian beban tiga fasa tipe Y dan Δ, aplikasi rangkaian sumber dan beban tiga fasa, serta penjelasan tentang tegangan fasa dan line to line pada sistem tiga fasa.

![Rangkaian sumber 1 fasaRangkaian sumber 1 fasa
Tinjau rangkaian sumber satu fasa sebagai berikut :
n
Vbn = 100∠-1200
V-rms
Vab
b
aa
-
+
Van = 100 ∠ 00
V-rms
VVabab = V= Vanan + V+ Vnbnb = VVabab – VVbnbn
= 100 ∠ 00
- 100∠-1200
= 100 (1 - 1∠-120o
)
=100 (1- (cos120o
– j sin 120o
))
= 100 (1 - (-1/2) + j (√3/2 ) )
= 100 (3/2) + j (√3/2 ))
Vab = 100[(3/2)2
+ (√3/2)2
]1/2
∠tan-1
{(√3/2)/(3/2)}
= 100[9/4 + 3/4]1/2
∠ tan-1
{1/√3}
= 100 √3∠ 30o
Vab
Vbn
Vnb
Van
Secara diagram fasor dapat dilihat pada
gambar disamping](https://image.slidesharecdn.com/rl-rangkaian3fasa-140601163602-phpapp01/75/RL-RANGKAIAN-3-FASA-2-2048.jpg)

![Three-phase electric powerThree-phase electric power
Three-phase electric powerThree-phase electric power is a common method ofis a common method of
alternating currentalternating current electric powerelectric power generationgeneration,,
transmissiontransmission, and, and distributiondistribution..[1][1]
It is a type ofIt is a type of
polyphase systempolyphase system and is the most common method usedand is the most common method used
byby gridsgrids worldwide to transfer power. It is also used toworldwide to transfer power. It is also used to
power largepower large motorsmotors and other large loads. Aand other large loads. A three-phasethree-phase
system is generally more economical than otherssystem is generally more economical than others
because it uses less conductor material to transmitbecause it uses less conductor material to transmit
electric power than equivalentelectric power than equivalent single-phasesingle-phase or two-or two-
phase systems at the same voltage.phase systems at the same voltage.[2][2]
The three-phaseThe three-phase
system was introduced and patented by Nikola Tesla insystem was introduced and patented by Nikola Tesla in
the years from 1887 to 1888.the years from 1887 to 1888.
http://en.wikipedia.org/wiki/Three-phase_electric_power](https://image.slidesharecdn.com/rl-rangkaian3fasa-140601163602-phpapp01/75/RL-RANGKAIAN-3-FASA-5-2048.jpg)