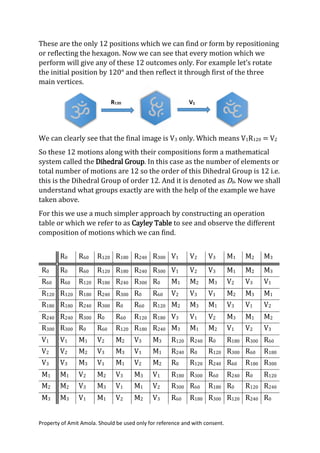
The document discusses groups in abstract algebra, focusing on dihedral groups and permutation groups. It explains the properties that define a group, such as closure, the existence of an identity element, and the presence of inverses, using examples like the dihedral group of a hexagon and symmetric groups of permutations. It also touches on notable terms in group theory, such as order of a group and subgroup, and highlights the significance of dihedral and symmetric groups in symmetry and permutations.








![Property of Amit Amola. Should be used only for reference and with consent.
Now let’s talk about inverse of these elements. Let’s find inverse of element
c.
c= (
1 2 3
3 1 2
) c-1= (
1 2 3
2 3 1
)
Thus, the inverse of an element is obtained by reading from the bottom
entry to the top entry rather than from top to bottom: if 1 appears beneath
3 in c then 3 appears beneath 1 in c-1.
So this was about symmetric group S3. Let’s talk little more about
Symmetric groups in general.
Symmetric Groups (Sn)
Let A= {1, 2, 3, …, n}. The set of all permutations of A is called the
symmetric group of degree n and is denoted by Sn. Elements of Sn have the
form
є= [
1 2
є(1) є(2)
… … … …
𝑛
є(n)]
It is easy to compute the order of Sn. There are n choices of є(1). Once є(1)
has been determined, there are (n-1) possibilities for є(2)[since є is one-to-
one, we must have є(1)≠ є(2)]. After choosing є(2), there are exactly (n-2)
possibilities for є(3). Continuing along in this fashion, we see that Sn must
have n(n-1)…3.2.1= n! elements.
Now, since S1 = {(1)} then S1 with respect to composition is commutative.
Similarly, since
[
1 2
1 2
] [
1 2
2 1
]= [
1 2
2 1
] [
1 2
1 2
]
then S2 = {[
1 2
1 2
] [
1 2
2 1
]}is also Abelian.
Unfortunately, this is not true anymore for |S| > 2.
We will now prove that Sn is not abelian when n≥3.](https://image.slidesharecdn.com/algebraarticle-150905062111-lva1-app6891/85/Introduction-to-Groups-and-Permutation-Groups-10-320.jpg)










