This document provides an overview of Unit II - Complex Integration from the Engineering Mathematics-IV course at RAI University, Ahmedabad. It covers key topics such as: 1) Complex line integrals and Cauchy's integral theorem which states that the integral of an analytic function around a closed curve is zero. 2) Cauchy's integral formula which can be used to evaluate integrals and find derivatives of analytic functions. 3) Taylor and Laurent series expansions of functions, including their regions of convergence. 4) The residue theorem which can be used to evaluate real integrals involving trigonometric or rational functions.

1. Complex Integration
Course- B.Tech
Semester-IV
Subject- ENGINEERING MATHEMATICS-IV
Unit- II
RAI UNIVERSITY, AHMEDABAD

2. Unit-II Complex Integration
Content
Definition of the complex line integral, Problem based on complex line integral, Cauchy’s
integral theorem(without proof), Cauchy’s integral formula for derivatives of analytic function,
problem based on Cauchy’s integral theorem & Cauchy’s integral formula, Expansion of
function in Power Series, Taylor’s series and Laurent’s series, singularities, Residue, find the
Residue of the function, Cauchy’s Residue theorem(Without proof) , Evaluation of real
integrals of the type ∫ (cos θ , sin θ) and ∫ ( )

3. Unit-II Complex Integration
1.1 Introduction—Complex variable techniques have been used in a wide variety of areas of
engineering. This has been particularly true in areas such as electromagnetic field theory, fluid
dynamics, aerodynamics and elasticity. With the rapid developments in computer technology
and the consequential use of sophisticated algorithms for analysis and design in engineering
there has been, in recent years, less emphasis on the use of complex variable techniques and a
shift towards numerical techniques applied directly to the underlying full partial differential
equations model of the situation. However it is useful to have an analytical solution, possibly
for an idealized model in order to develop a better understanding of the solution and to develop
confidence in numerical estimates for the solution of more sophisticated models.
1.2 Applications— The design of aerofoil sections for aircraft is an area where the theory was
developed using complex variable techniques. Throughout engineering, transforms defined as
complex one form or another play a major role in analysis and design. The use of complex
variable techniques allows us to develop criteria for the stability of systems.
1.3 Complex line integral—If ( ) is a single-valued, continuous function in some region R in
the complex plane then we define the integral of ( ) along a path C in R as shown in figure—
( ) = ( + )( + )
( ) = ( − ) + ( + )
Example— Obtain the complex integral ∫ where C is the straight line path from
= + to = + as shown in figure—
Solution— for the straight line path C—
= , =
= ( + )( + )

4. Unit-II Complex Integration
= ( + )( + ) = (1 + ) = 2
2
= 8
Example—
Obtain the complex integral ∫ z dz where C is the part of the unit circle going anticlockwise
from the point z = 1 to z = i as shown in igure—
Solution— we know that—
= , for unit circle C in first quadrant, = 1, 0 ≤ ≤
Hence—
z dz = = = =
3
=
cos 3 + sin 3
3
= −
1
3
(1 + )
Example— Obtain the complex integral ∫ dz where C is a unit circle.
Solution— we know that— z = re , Since, C is a unit circle, so = 1 and 0 ≤ ≤ 2
Hence,
1
z
dz =
1
e
ie θ
dθ = i dθ = 2 i

5. Unit-II Complex Integration
Exercises
1. Obtain the integral ∫ z dz along the straight − line path from z = 2 + 2i to z = 5 + 2i.
(a) from = 2 + 2 to = 5 + 2
(b) from = 5 + 2 to = 5 + 5
(c) from = 2 + 2 to = 5 + 5
2. Find ∫ (z + z)dz where C is the part of the unit circle going anti − clockwise from the
point z = 1 to the point z = i.
3. Find ∫ ( ) , where C is the circle | – 1 − | = 1 and ( ) = 1/( − 1 – ).
(a) ( ) = 1/ , = 1
(b) ( ) = 1/( − 1) , = 1
(c) ( ) = 1/( − 1 – ), = 1 +
1.4 The Cauchy’s integral theorem— If a function ( ) is analytic and its derivative ( )
continuous at each point inside and on a closed curve C then—
( ) =
Let a region R bounded by a simple closed curve C, Let ( ) = + , = +
Hence—
( ) = ( − ) + ( + )
Since, ( ) is continuous in region R, by using Green’s theorem—
( ) = − − + −
Again, as ( ) is a analytic function in the region R, from C-R equations—
= and = −
Hence—
( ) = 0

6. Unit-II Complex Integration
1.4 The Cauchy’s integral formula— If ( ) is analytic within and on a closed curve C
having a point within the curve C then—
( ) =
1
2
( )
−
Or
( )
−
= 2 ( )
1.5 The Cauchy’s integral formula for derivatives of analytic function— If a function ( )
is analytic in a region R, then its derivative at any point = of R is also analytic in R and it is
given by—
( ) =
1
2
( )
( − )
Similarly—
′′( ) =
2!
2
( )
( − )
′′′( ) =
3!
2
( )
( − )
Hence—
( ) =
!
2
( )
( − )
Example— Find ∮ where the contour C contains the point = and exclude
the point = − .
Solution—∮ = ∮
Now, from the question contour C include the point = and exclude the
point = − . Hence, ( ) = will be analytic function within C.
Therefore, by using Cauchy’s integral formula—
sinh
+
2
=
( )
−
2
= 2
2
= 2
ℎ
2
2
+
2
= 2 = 2 sin = 2

7. Unit-II Complex Integration
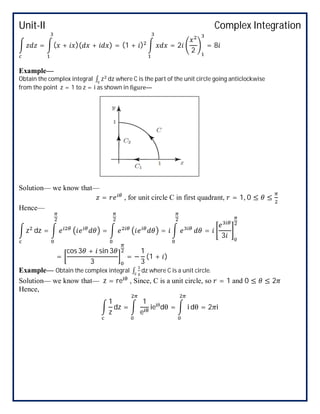
Example— Find ∮ ( )( )
where the contour C: | | = .
Solution— to evaluate ∮ ( )( )
Poles are given by (3 + 1)( − 3) = 0 ⇒ = 0, − , 3
The poles = 0 and = − lies within the contour C: | | = 1 and the pole = 3 lies outside
the contour C: | | = 1.
Hence ( ) = is analytic within C. therefore—
(3 + 1)( − 3)
=
( )
(3 + 1)
=
( )
− 3
( )
(3 + 1)
= ∮
( )
− ∮
( )
= 2 (0) − 2 [by Cauchy’s integral formula]
= 2 − =
Example— Find ∮ ( )
where the contour C: | − | = .
Solution— here, ( − 3) = 0 ⇒ = 3 (Pole of order 3)
Again, C: | − 2| = 1 , the point = 3 lies on C.
Hence, ( ) = is analytic in C. therefore by Cauchy’s integral formula—
( − 3)
=
2
2!
(3) =
1.6 Taylor’s Theorem for Complex Variables— Let ( ) be analytic on the region
| − | < . Then –
( ) =
( )
!
( − )
The right-hand side is the Taylor series for ( ) at = , and its radius of convergence is
| − | < .
Example— Expand in powers of ( − ).
Solution— let ( ) = log .
( ) = , ( ) = , ( ) =
∴ ( ) =
(−1) ( − 1)!
, = 1,2,3 …
From Taylor’s series—
( ) =
( )
!
( − )

8. Unit-II Complex Integration
From the question ( ) = log and = 1, hence—
log =
(1)
!
( − 1)
log = (1) +
(1)
!
( − 1)
log = log 1 +
(−1) ( − 1)!
!
( − 1)
log =
(−1)
( − 1)
For the region of convergence—
As = 0 is a singular point. ∴ R = | − | [ is a singular point ]
R = |1 − 0| = 1
Hence region of convergence is | − 1| < 1.
Example— Expand ( ) = ( )
.
Solution— we know that = ∑ , | | < 1
On differentiating—
1
1 −
=
1
(1 − )
= = ( + 1)
Region of convergence is | | < 1.
Example— Expand ( ) = .
Solution— given that ( ) = sin
( ) =
√
By using binomial theorem—
( ) =
1
√1 −
= 1 +
1
2
+
3
8
+
5
16
+ ⋯
On integrating—
sin = +
1
6
+
3
40
+
5
112
+ ⋯
Region of convergence—
For principle value of sin , Re{sin } < .

9. Unit-II Complex Integration
1.7 Laurent’s Theorem for Complex Variables— If ( ) is analytic in the annular region R
given by R < |z − z | < R , then ( ) can be represented by the convergent series—
( ) = A ( − )
Where
A = ∮
( )
( )
dz, n = 0, ±1, ±2, ±3 …
Where C is any positively oriented simple closed contour lying in region R given by –
| − | = R and R < < R .
Example— Find all possible expansions of ( ) = about = .
Solution— here, = − is a singular point and = 0 is a regular point.
∴ R = |z − a| = |0 − (−i)| = 1
Hence, there exists a Taylor series of ( ) in | | < 1 about = 0 and a Laurent series in the
annulus 1 < | | < ∞
Taylor’s series (| | < 1)
1
+
=
1
(1 − )
=
−
(1 − )
= − (1 − )
= − [1 + − − + + ⋯ ]
= − + + + − + ⋯
Laurent’s series ( < | | < ∞) ⇒ | |
< 1
Hence,
1
+
=
1
1 +
=
1
1 + =
1
1 − −
1
+ ⋯
1
+
=
1
− −
1
+ ⋯ , (1 < | | < ∞)
Example— Expand
( )
about = for the regions
(1) < | | < 1 (2) < | | < 2 (3) | | =
Solution—
Let ( ) =
( )
= ( )( )
[Singular points are = 0,1,2]
∴ ( ) = −
( )
+
( )
(1) for < | | < 1
( ) =
1
2
−
1
( − 1)
+
1
2( − 2)
=
1
2
+ (1 − ) −
1
4
1 −
2
( ) =
1
2
+ (1 + + + + ⋯ ) −
1
4
1 +
2
+
4
+
8
+ ⋯
( ) =
1
2
+
3
4
+
7
8
+
15
16
+
31
32
+ ⋯

10. Unit-II Complex Integration
(2) for 1 < | | < 2
( ) =
1
2
−
1
( − 1)
+
1
2( − 2)
=
1
2
−
1
1 −
1
−
1
4
1 −
2
( ) =
1
2
−
1
1 +
1
+
1
+
1
+ ⋯ −
1
4
(1 +
2
+
4
+
8
+ ⋯ )
( ) = −
1
2
−
1
−
1
−
1
− ⋯ −
1
4
(1 +
2
+
4
+
8
+ ⋯ )
(3) for | | > 2
( ) =
1
2
−
1
( − 1)
+
1
2( − 2)
=
1
2
−
1
1 −
1
+
1
2
1 −
2
( ) =
1
2
−
1
1 +
1
+
1
+
1
+ ⋯ +
1
2
1 +
2
+
4
+
8
+ ⋯
( ) = −
1
2
−
1
−
1
−
1
− ⋯ +
1
2
+
1
+
2
+
4
+ ⋯ =
1
+
3
+
7
+ ⋯
1.7 Residue Theory—
1.7.1 Residue—Residue of an analytic function ( ) at an isolated singular point = is
the coefficient says of ( − ) in the Laurent series expansion of ( ) about . It is
denoted by =
Res
=
( ).
From Laurent series—
=
Res
=
( ) =
1
2
( )
1.7.2 Calculation of residues—
1. at simple pole— Residue of an analytic function ( ) at an isolated singular
point of order ( = 1) is given by—
=
lim
→
( − ) ( )
2. at multiple pole— Residue of an analytic function ( ) at an isolated singular
point of order ( = > 1) is given by—
=
1
( − 1)!
lim
→
d
dz
[( − ) ( )]
3. at an essential singularity— Residue of an analytic function ( ) at an
essential singularity = can be evaluated in following steps—
Step-I Rewrite ( ) in terms of ( − ) by using Laurent series
and Taylors series.
Step-II required value of residue is the coefficient of
( )
in the
power series.

11. Unit-II Complex Integration
1.7.3 Cauchy’s Residue Theorem— If ( ) is an analytic function within and on a simple
closed path C except at a finite number of singular points , , , … , inside C, then—
( ) = 2 ( + + + ⋯ + )
Example— Determine the residues at the poles of ( )( )
.
Solution— let ( ) = ( )( )
=
( )
( )( )( )
Hence poles are given by—
= −4, −2 and 4
Now,
Residue at = −4
=
→ −4
( + 4)
( )
( )( )( )
=
→ −4
( )
( )( )
=
Residue at = −2
=
→ −2
( + 2)
( )
( )( )( )
=
→ −2
( )
( )( )
=
Residue at = 4
=
→ 4
( − 4)
( )
( )( )( )
=
→ 4
( )
( )( )
=
Example— Evaluate = ∮ , where C is a circle | | = .
Solution— given that I = ∮ sin
Here, = 0 is an essential singular point lying within the contour C: | | = .
Now,
= 1 + + + + ⋯
= 1 − + − + ⋯
= 1 − + − + ⋯
and sin = − + − ⋯
sin = − + − ⋯
Hence, = 1 − + − + ⋯ − + − ⋯
= − + ⋯
Therefore residue= the coefficient of in the expansion of = 1
Thus, I = ∮ sin = 2π

12. Unit-II Complex Integration
1.8 Evaluation of real definite integral of rational function of and -
By integration around a unit circle—
Let I = ∫ F(cos θ, sin θ)dθ
We know that—
cos = , sin = and = ⇒ =
Hence, I = ∫ F(cos θ, sin θ)dθ = ∮ ( )
Let ( ) =
( )
which is analytic in region of unit circle.
Therefore by using Cauchy’s residue theorem—
I = F(cos θ, sin θ)dθ = 2πi Res H(z)
Where the summation is taken for all poles of ( ) which are within the unit circle
C:| | = 1.
Example— Evaluate I = ∫ , |p| < 1.
Solution— let = and by putting = and sin =
Hence, I = ∫ = ∮
= − ∮ ( )
Where C:| | = 1
This has simple poles at = and = .
Again, as | | < 1, so the pole = lies inside and = outside the contour C.
Therefore, residue is given by—
=
Res
=
( ) =
lim
→
( − ) ( )( )
= ( )
=
=
Hence,
I = ∫ , |p| < 1
= − (2 )
=

13. Unit-II Complex Integration
1.9 Evaluation of improper real integral (of first kind) of rational function—
By integration around a semi-circle—
( ) = 2 (residues of ( )at all the poles of ( )in the upper half circle)
Example— Evaluate I = ∫ ( )
Solution— = ∫ ( )
= ∫ ( )
For poles—
( + 9) = 0 ⇒ = ±3 (Poles of order 2)
Here only = 3 lies on upper half plane.
Hence,
=
Res
z → 3
( − 3 )
( )
=
Res
→ 3 ( )
=
Res
→ 3 ( )
=
Res
→ 3
( ) ( )
( )
=
Res
→ 3 ( )
= 0
Therefore—
I = ∫ ( )
= 2 ( ) = 0

14. Unit-II Complex Integration
References—
1. Internet—
1.1 mathworld.wolfram.com
1.2 www.math.com
1.3 www.grc.nasa.gov
1.4 en.wikipedia.org/wiki/Conformal_map
1.5 http://www.webmath.com/
1.6 http://www.personal.soton.ac.uk/
1.7 http://www.math.columbia.edu/
2. Journals/Paper/notes—
2.1 Complex variables and applications-Xiaokui Yang-Department of Mathematics, Northwestern University
2.2 Conformal Mapping and its Applications-Suman Ganguli-Department of Physics, University of Tennessee, Knoxville, TN 37996-
November 20, 2008
2.3 Conformal Mapping and its Applications-Ali H. M. Murid-Department of Mathematical Sciences-Faculty of Science-University
Technology Malaysia -81310-UTM Johor Bahru, Malaysia-September 29, 2012
2.4 HELM (VERSION 1: March 18, 2004): Workbook Level 2, 26.4: Basic Complex Integration
3. Books—
3.1 Higher Engineering Mathematics-Dr. B.S. Grewal- 42nd edition-Khanna Publishers-page no 639-672
3.2 Higher Engineering Mathematics- B V RAMANA- Nineteenth reprint-McGraw Hill education (India) Private limited- page no 22.1-25.26
3.3 Complex analysis and numerical techniques-volume-IV-Dr. Shailesh S. Patel, Dr. Narendra B. Desai- Atul Prakashan
3.4 A Text Book of Engineering Mathematics- N.P. Bali, Dr. Manish Goyal- Laxmi Publications(P) Limited- page no 1033-1100