The document provides an extensive overview of integral calculus, emphasizing the integration process as the reverse of differentiation, and introducing key concepts such as indefinite and definite integrals, properties, and methods of integration. It details various integration techniques, including polynomial division and partial fraction expansion, along with numerous example problems demonstrating the application of these methods. Additionally, the document lists several standard integrals and antiderivatives for common functions.

1. Integral Calculus
The integral of a function 𝑓(𝑥) with respect to 𝑥 is written as 𝑓(𝑥)𝑑𝑥
The integration is defined as the reverse process of differentiation and is
sometimes termed as anti-derivative.
This means that if
𝑑
𝑑𝑥
𝑔 𝑥 = 𝑓(𝑥) then 𝑓(𝑥)𝑑𝑥 = 𝑔 𝑥 + 𝑐 ,
where c, called the constant of integration, is really necessary.
Thus if g 𝑥 is differential function of 𝑥 such that
𝑑
𝑑𝑥
𝑔 𝑥 = 𝑓(𝑥)
then g 𝑥 is called anti-derivative or primitive or an indefinite integral
or simply an integral of 𝑓 (𝑥).

2. Integration is like filling a water can from a tap.
The input (before integration) is the flow rate from the tap.
Integrating the flow (adding up all the little bits of water) gives us the volume of
water in the can.

4. Suppose the can already has water in it , let it be "𝑐" value, which gives us to
always add " + 𝑐 ".
The integral of the flow rate 2𝑥 tells us the volume of water 2𝑥 𝑑𝑥 = 𝑥2 + 𝑐
And the slope of the volume increase 𝑥2 + 𝑐 gives us back the flow rate
𝑑
𝑑𝑥
(𝑥2 + 𝑐) = 2𝑥

5. Definite Integral
Indefinite Integral

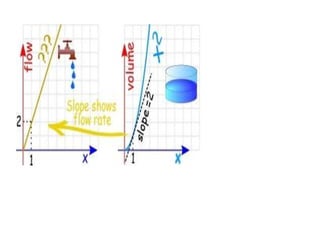
6. Properties of the Indefinite Integral
If a is some constant, then 𝑎𝑓(𝑥)𝑑𝑥 = 𝑎 𝑓(𝑥)𝑑𝑥,
i.e. the constant coefficient can be carried outside the integral sign.
For functions 𝑓 𝑥 𝑎𝑛𝑑 𝑔 𝑥 ,
[𝑓(𝑥) ± 𝑔(𝑥)]𝑑𝑥 = 𝑓(𝑥)𝑑𝑥 ± 𝑔(𝑥)𝑑𝑥,
i.e. the indefinite integral of the sum (difference) equals to the sum (difference) of
the integrals.

7. 𝒂𝒅𝒙 = 𝒂𝒙 + 𝑪
𝒙𝒅𝒙 =
𝒙𝟐
𝟐
+ 𝑪
𝒙𝟐
𝒅𝒙 =
𝒙𝟑
𝟑
+ 𝑪 𝑥𝑛
𝑑𝑥 =
𝑥𝑛+1
𝑛+1
+ 𝐶
𝟏
𝒙
𝒅𝒙 = 𝒍𝒐𝒈|𝒙| + 𝑪 𝑒𝑥
𝑑𝑥 = 𝑒𝑥
+ 𝐶
𝒂𝒙
𝒅𝒙 =
𝒂𝒙
𝒍𝒐𝒈𝒂
+ 𝑪 𝑠𝑖𝑛𝑥𝑑𝑥 = −𝑐𝑜𝑠𝑥 + 𝐶
𝒄𝒐𝒔𝒙𝒅𝒙 = 𝒔𝒊𝒏𝒙 + 𝑪 𝑡𝑎𝑛𝑥𝑑𝑥 = −𝑙𝑜𝑔|𝑐𝑜𝑠𝑥| + 𝐶
𝒄𝒐𝒕𝒙𝒅𝒙 = 𝒍𝒐𝒈|𝒔𝒊𝒏𝒙| + 𝑪 𝑠𝑒𝑐𝑥 𝑑𝑥 = 𝑙𝑜𝑔 ∣ 𝑡𝑎𝑛
𝑥
2
+
𝜋
4
∣ +𝐶 = 𝑙𝑜𝑔|𝑠𝑒𝑐𝑥 + 𝑡𝑎𝑛𝑥| + 𝐶
𝒄𝒐𝒔𝒆𝒄𝒙 𝒅𝒙 = 𝒍𝒐𝒈 ∣ 𝐭𝐚𝐧
𝒙
𝟐
∣ +𝑪 = −𝒍𝒐𝒈|𝒄𝒐𝒔𝒆𝒄𝒙 + 𝒄𝒐𝒕𝒙| + 𝑪 sec2
𝑥 𝑑𝑥 = 𝑡𝑎𝑛𝑥 + 𝐶
𝒄𝒐𝒔𝒆𝒄𝟐
𝒙 𝒅𝒙 = −𝒄𝒐𝒕𝒙 + 𝑪 𝑠𝑒𝑐𝑥 𝑡𝑎𝑛𝑥𝑑𝑥 = 𝑠𝑒𝑐𝑥 + 𝐶
𝒄𝒐𝒔𝒆𝒄𝒙 𝒄𝒐𝒕𝒙 𝒅𝒙 = −𝒄𝒐𝒔𝒆𝒄𝒙 + 𝑪 𝑑𝑥
1+𝑥2 = tan−1
𝑥 + 𝐶 = 𝑎𝑟𝑐𝑡𝑎𝑛𝑥 + 𝐶
𝒅𝒙
𝒂𝟐+𝒙𝟐 =
𝟏
𝒂
𝐭𝐚𝐧−𝟏 𝒙
𝒂
+ 𝑪 =
𝟏
𝒂
𝐚𝐫𝐜𝐭𝐚𝐧
𝒙
𝒂
+ 𝑪 𝑑𝑥
1−𝑥2 =
1
2
𝑙𝑜𝑔 ∣
1+𝑥
1−𝑥
∣ +𝐶
𝒅𝒙
𝒂𝟐−𝒙𝟐 =
𝟏
𝟐𝒂
𝒍𝒐𝒈 ∣
𝒂+𝒙
𝒂−𝒙
∣ +𝑪
𝑑𝑥
1−𝑥2
= sin−1
𝑥 + 𝐶 = 𝑎𝑟𝑐𝑠𝑖𝑛𝑥 + 𝐶
𝒅𝒙
𝒂𝟐−𝒙𝟐
= 𝐬𝐢𝐧−𝟏 𝒙
𝒂
+ 𝑪 = 𝐚𝐫𝐜𝐬𝐢𝐧
𝒙
𝒂
+ 𝑪
𝑑𝑥
𝑥2±𝑎2
= 𝑙𝑜𝑔 ∣ 𝑥 + 𝑥2 ± 𝑎2 ∣ +𝐶
𝒅𝒙
𝒙 𝒙𝟐−𝟏
= 𝐬𝐞𝐜−𝟏
𝒙 + 𝑪 = 𝒂𝒓𝒄𝒔𝒆𝒄|𝒙| + 𝑪 𝑠𝑖𝑛ℎ𝑥𝑑𝑥 = 𝑐𝑜𝑠ℎ𝑥 + 𝐶
𝒄𝒐𝒔𝒉𝒙𝒅𝒙 = 𝒔𝒊𝒏𝒉𝒙 + 𝑪 𝑠𝑒𝑐ℎ2𝑥𝑑𝑥 = 𝑡𝑎𝑛ℎ𝑥 + 𝐶
𝒄𝒐𝒔𝒆𝒄𝒉𝟐𝒙𝒅𝒙 = −𝒄𝒐𝒕𝒉𝒙 + 𝑪 𝑠𝑒𝑐ℎ𝑥𝑡𝑎𝑛ℎ𝑥𝑑𝑥 = −𝑠𝑒𝑐ℎ𝑥 + 𝐶
𝒄𝒐𝒔𝒆𝒄𝒉𝒙𝒄𝒐𝒕𝒉𝒙𝒅𝒙 = −𝒄𝒐𝒔𝒆𝒄𝒉𝒙 + 𝑪 𝑡𝑎𝑛ℎ𝑥𝑑𝑥 = 𝑙𝑛𝑐𝑜𝑠ℎ𝑥 + 𝐶

8. 1
𝑥𝑛 𝑑𝑥 =
1
−𝑛+1 𝑥−𝑛+1 + 𝐶
𝑎𝑥 ± 𝑏 𝑛𝑑𝑥 =
𝑎𝑥±𝑏 𝑛+1
𝑎 𝑛+1
𝑑𝑥
𝑎𝑥± 𝑏
=
1
𝑎
log 𝑎𝑥 ± 𝑏 + 𝐶
sin 𝑎𝑥 ± 𝑏 𝑑𝑥 = −
cos 𝑎𝑥±𝑏
𝑎
+ 𝐶
cos 𝑎𝑥 ± 𝑏 𝑑𝑥 =
sin 𝑎𝑥±𝑏
𝑎
+ 𝐶
𝑒𝑎𝑥±𝑏
𝑑𝑥 =
𝑒𝑎𝑥±𝑏
𝑎
+ 𝐶
𝑑𝑥
𝑎𝑥±𝑏 𝑛 =
1
𝑎 −𝑛+1 𝑎𝑥±𝑏 −𝑛+1 + 𝐶

9. Methods of integration
Method 1. Integrals of functions of the form
(i) 𝒇 𝒙
𝒏
𝒇′ 𝒙 𝒅𝒙 =
𝒇 𝒙
𝒏+𝟏
𝒏+𝟏
+ 𝑪
(OR)
Put 𝑡 = 𝑓(𝑥) , 𝑑𝑡 = 𝑓’(𝑥) 𝑑𝑥 and 𝑡𝑛 𝑑𝑡 =
𝑡𝑛+1
𝑛+1
+ 𝐶
(ii)
𝒇′ 𝒙 𝒅𝒙
𝒇 𝒙
𝒏 = −
𝟏
𝒇 𝒙
𝒏−𝟏 + 𝑪
(OR)
Put 𝑡 = 𝑓(𝑥) , 𝑑𝑡 = 𝑓’(𝑥) 𝑑𝑥 and
𝑑𝑡
𝑡𝑛 = −
1
𝑡𝑛−1 + 𝐶
Note : when 𝑛 = −1 𝑖𝑛 𝑖 𝑂𝑅 𝑛 = 1 𝑖𝑛 (𝑖𝑖) ,
𝑓′ 𝑥
𝑓 𝑥
𝑑𝑥 = 𝑙𝑜𝑔 𝑓 𝑥 + 𝐶
Problem 1: Find 𝐜𝐨𝐬𝟑 𝒙 𝒔𝒊𝒏𝒙 𝒅𝒙
Solution:
Here we take t = 𝑓 𝑥 = 𝑐𝑜𝑠𝑥 , dt = 𝑓′
𝑥 = 𝑠𝑖𝑛𝑥
cos3
𝑥 𝑠𝑖𝑛𝑥 𝑑𝑥 = 𝑓 𝑥
3
𝑓′
𝑥 𝑑𝑥 =
𝑓 𝑥
3+1
3+1
+ 𝐶 =
𝑓 𝑥
4
4
+ 𝐶

10. Problem 2: Find 𝐭𝐚𝐧 𝒙 𝐬𝐞𝐜𝟐
𝒙 𝒅𝒙
Solution:
Here we take 𝑡 = 𝑡𝑎𝑛𝑥 ⟹ 𝑑𝑡 = sec2 𝑥 𝑑𝑥
𝑡𝑎𝑛𝑥𝑠𝑒𝑐2
𝑥𝑑𝑥 = 𝑡 𝑑𝑡 =
𝑡2
2
+ 𝐶
=
𝑡𝑎𝑛𝑥 2
2
+ 𝐶
Problem 3: Find 𝒄𝒐𝒔𝟐𝒙𝒔𝒊𝒏𝟐𝒙𝒅𝒙
Solution:
Here we take 𝑡 = 𝑠𝑖𝑛2𝑥 ⇒ 𝑑𝑡 = 𝑐𝑜𝑠2𝑥 2 𝑑𝑥 ⇒ 𝑐𝑜𝑠2𝑥 𝑑𝑥 =
𝑑𝑡
2
𝑐𝑜𝑠2𝑥𝑠𝑖𝑛2𝑥𝑑𝑥 = 𝑡
𝑑𝑡
2
=
1
2
𝑡𝑑𝑡 =
1
2
.
𝑡2
2
=
𝑡2
4
=
𝑠𝑖𝑛2𝑥 2
4
+ 𝐶
Problem 4: Find
𝟐𝒙
𝒙𝟐−𝟒
𝟐 𝒅𝒙
Solution:
Here we take 𝑡 = 𝑥2
− 4 ⇒ 𝑑𝑡 = 2𝑥 𝑑𝑥
2𝑥
𝑥2−4 2 𝑑𝑥 =
𝑑𝑡
𝑡2 = −
1
𝑡
+ 𝐶 = −
1
𝑥2−4
+ 𝐶

11. Problem 5: Evaluate
𝒄𝒐𝒔𝜽
𝐬𝐢𝐧𝟑 𝜽
𝒅𝜽
Solution:
Here we take 𝑡 = 𝑠𝑖𝑛𝜃 ⟹ 𝑑𝑡 = 𝑐𝑜𝑠𝜃 𝑑𝜃
𝑐𝑜𝑠𝜃
sin3 𝜃
𝑑𝜃 =
𝑑𝑡
𝑡3 = −
1
𝑡2 + 𝐶 = −
1
sin2 𝜃
+ 𝐶
Problem 6: Evaluate
𝒙𝟑
𝟒+𝒙𝟐
𝒅𝒙
Solution:
Here we take 𝑡 = 4 + 𝑥2
⟹ 𝑑𝑡 = 2𝑥 𝑑𝑥 ⇒ 𝑥𝑑𝑥 =
𝑑𝑡
2
And 𝑥2
= 𝑡 − 4
𝑥3𝑑𝑥
4+𝑥2
=
𝑥2.𝑥𝑑𝑥
4+𝑥2
=
𝑡−4
𝑑𝑡
2
𝑡
=
1
2
𝑡−4
𝑡
1
2
𝑑𝑡 =
1
2
𝑡 − 4 𝑡−
1
2𝑑𝑡

12. =
1
2
(𝑡1𝑡−
1
2 − 4𝑡−
1
2)𝑑𝑡 =
1
2
𝑡1−
1
2 𝑑𝑡 − 4 𝑡−
1
2 𝑑𝑡
=
1
2
𝑡
1
2𝑑𝑡 − 4 𝑡−
1
2 𝑑𝑡
=
1
2
𝑡
1
2
+1
1
2
+1
− 4
𝑡
−
1
2
+1
−
1
2
+1
=
1
2
𝑡
3
2
3
2
− 4
𝑡
1
2
1
2
=
1
2
2
3
𝑡
3
2 − 4
2
1
𝑡
1
2
=
1
3
𝑡
3
2 − 4 𝑡
1
2 =
1
3
4 + 𝑥2
3
2 − 4 4 + 𝑥2
1
2

13. Method 2 -Integration of rational algebraic functions
Type I. If the degree of the numerator is equal or greater than the degree of the
denominator, divide the numerator by the denominator and then integrate.
(i.e) Polynomial Division: Divide the denominator into the numerator (if needed) to
write the integrand as a polynomial plus a proper rational function.
Type II. Partial Fraction Expansion: Expand the proper rational function using
partial fractions. (If the denominator can be resolved into rational factors)
Type III. Completing the Square: If any terms involve quadratics, eliminate the
linear term if needed by completing the square. (denominator is of second degree
and does not resolve into rational factors)
Type IV. Term by Term Integration: Use elementary integral formulas and
substitution.

14. Type – I(Method 2) –Polynomial Division: The degree of
the numerator is equal or greater than the degree of the
denominator-Integration of the form
𝒂𝟏𝒙𝟑+𝒃𝟏𝒙𝟐+𝒄𝟏𝒙+𝒅𝟏
𝒂𝟐𝒙𝟐+𝒃𝟐𝒙+𝒄𝟐
𝒅𝒙
Problem 1: Evaluate
𝒙𝟐𝟒
𝒙𝟏𝟎+𝟏
𝒅𝒙
Solution:
𝑥14
− 𝑥4
𝑥10
+ 1 𝑥24
𝑥24
+ 𝑥14
(−) (−)
----------------------
− 𝑥14
−𝑥14
− 𝑥4
(+) (+)
---------------------------------
𝑥4

15. Hence
𝑥24
𝑥10+1
= 𝑥14 − 𝑥4 +
𝑥4
𝑥10+1
𝑥24 𝑑𝑥
𝑥10+1
= 𝑥14
− 𝑥4
+
𝑥4
𝑥10+1
𝑑𝑥
= 𝑥14
𝑑𝑥 − 𝑥4
𝑑𝑥 +
𝑥4
𝑥10+1
𝑑𝑥 ------ (1)
Consider
𝑥4
𝑥10+1
𝑑𝑥 =
𝑥4
𝑥2.5+1
𝑑𝑥 =
𝑥4 𝑑𝑥
𝑥5 2 +1
----- (2)
Put 𝑥5
= 𝑡 ⇒ 5 𝑥4
𝑑𝑥 = 𝑑𝑡 ⇒ 𝑥4
𝑑𝑥 =
𝑑𝑡
5
(2)⇒
𝑥4
𝑥10+1
𝑑𝑥 =
𝑑𝑡
5
𝑡2+1
=
1
5
𝑑𝑡
𝑡2+1
=
1
5
tan−1 𝑡 =
1
5
𝑡𝑎𝑛−1(𝑥5) ---- (3)
Using (3) in (1)
𝑥4
𝑥10+1
𝑑𝑥 = 𝑥14𝑑𝑥 − 𝑥4𝑑𝑥 +
𝑥4
𝑥10+1
𝑑𝑥
=
𝑥15
15
−
𝑥5
5
+
1
5
tan−1
𝑥5
+ 𝐶

16. Type II (Method 2). Evaluate Integral by using partial fraction method
If the denominator can be resolved into rational factors, the method of partial
fraction is to be used
Type 1.
𝒅𝒙
𝒂𝟏𝒙+𝒃𝟏 𝒂𝟐𝒙+𝒃𝟐
Step 1. Take
𝟏
𝒂𝟏𝒙+𝒃𝟏 𝒂𝟐𝒙+𝒃𝟐
=
𝑨
𝒂𝟏𝒙+𝒃𝟏
+
𝑩
𝒂𝟐𝒙+𝒃𝟐
Step 2. Find the value of A and B from step 1
Step 3. Substitute the value of A and B and then integrate
Type 2.
𝒅𝒙
𝒂𝟏𝒙+𝒃𝟏
𝟐 𝒂𝟐𝒙+𝒃𝟐
Step 1. Take
𝟏
𝒂𝟏𝒙+𝒃𝟏
𝟐 𝒂𝟐𝒙+𝒃𝟐
=
𝑨
𝒂𝟏𝒙+𝒃𝟏
+
𝑩
𝒂𝟏𝒙+𝒃𝟏
𝟐 +
𝑪
𝒂𝟐𝒙+𝒃𝟐
Step 2. Find the value of A,B and C from step 1
Step 3. Substitute the value of A,B and C and then integrate
Type 3.
𝒅𝒙
(𝒂𝟏𝒙+𝒃𝟏)(𝒂𝟐𝒙𝟐+𝒃𝟐𝒙+𝒄𝟐 )
Step 1. Take
𝟏
𝒂𝟏𝒙+𝒃𝟏 𝒂𝟐𝒙𝟐+𝒃𝟐𝒙+𝒄𝟐
=
𝑨
𝒂𝟏𝒙+𝒃𝟏
+
𝑩𝒙+𝒄
𝒂𝟐𝒙𝟐+𝒃𝟐𝒙+𝒄𝟐
Step 2. Find the value of A,B and C from step 1
Step 3. Substitute the value of A,B and C and then integrate

17. Problem 1: Evaluate
𝟏+𝟔𝒙
𝟒𝒙−𝟑 𝟐𝒙+𝟓
𝒅𝒙
Solution:
Consider
1+6𝑥
4𝑥−3 2𝑥+5
=
𝐴
4𝑥−3
+
𝐵
2𝑥+5
------ (1)
1 + 6𝑥 = 𝐴 2𝑥 + 5 + 𝐵(4𝑥 − 3) ------- (2)
Put 𝑥 = −
5
2
in (2)
⟹ 1 + 6𝑥 = 𝐴 2𝑥 + 5 + 𝐵(4𝑥 − 3)
⇒ 1 + 6 −
5
2
= 𝐴 2 −
5
2
+ 5 + 𝐵 4 −
5
2
− 3
⇒ 1 − 3 −5 = 𝐴 −5 + 5 + 𝐵 2 −5 − 3
⇒ 1 + 15 = 𝐴 0 + 𝐵 −10 − 3
⇒ 16 = −13𝐵
⇒ 𝐵 = −
16
13
Put 𝑥 =
3
4
in (2)
⇒ 1 + 6
3
4
= 𝐴 2
3
4
+ 5 + 𝐵 4
3
4
− 3
⇒ 1 + 3
3
2
= 𝐴
3
2
+ 5 + 𝐵 3 − 3
⇒ 1 +
9
2
=
𝐴 3+10
2
+ 𝐵 0
⇒
2+9
2
= 𝐴
13
2
⇒ 11 = 𝐴 13
⇒ 𝐴 =
11
13

18. (1) ⇒
1+6𝑥
4𝑥−3 2𝑥+5
=
𝐴
4𝑥−3
+
𝐵
2𝑥+5
=
11
13
4𝑥−3
+
−
16
13
2𝑥+5
=
11
13
1
4𝑥−3
−
16
13
1
2𝑥+5
1+6𝑥 𝑑𝑥
4𝑥−3 2𝑥+5
=
11
13
1
4𝑥−3
𝑑𝑥 −
16
13
1
2𝑥+5
𝑑𝑥
=
11
13
𝑑𝑥
4𝑥−3
−
16
13
𝑑𝑥
2𝑥+5
=
11
13
1
4
log 4𝑥 − 3 −
16
13
1
2
log 2𝑥 + 5 + 𝐶 , ∵
𝑑𝑥
𝑎𝑥±𝑏
=
1
𝑎
log 𝑎𝑥 ± 𝑏
=
11
52
log 4𝑥 − 3 −
16
26
log 2𝑥 + 5 + 𝐶
Problem 2: Evaluate
𝒙𝒅𝒙
𝒙−𝟏 𝟐 𝒙+𝟐
Solution:
Consider
𝑥
𝑥−1 2 𝑥+2
=
𝐴
𝑥−1
+
𝐵
𝑥−1 2 +
𝐶
𝑥+2
------(1)
⇒ 𝑥 = 𝐴 𝑥 − 1 𝑥 + 2 + 𝐵 𝑥 + 2 + 𝐶 𝑥 − 1 2
------(2)
Put 𝑥 = 1 in (2)
⇒ 1 = 𝐴 1 − 1 1 + 2 + 𝐵 1 + 2 + 𝐶 1 − 1 2
⇒ 1 = 𝐴 0 + 𝐵 3 + 𝐶(0)
⇒ 1 = 3𝐵 ⇒ 𝐵 =
1
3
Put 𝑥 = −2 in (2)
⇒ −2 = 𝐴 −2 − 1 −2 + 2 + 𝐵 −2 + 2 + 𝐶 −2 − 1 2
⇒ −2 = 𝐴 0 + 𝐵 0 + 𝐶 −3 2
⇒ −2 = 9𝐶 ⇒ 𝐶 = −
2
9
Put 𝑥 = 0 in (2)
⇒ 0 = 𝐴 0 − 1 0 + 2 + 𝐵 0 + 2 + 𝐶 0 − 1 2
⇒ 0 = −2𝐴 + 2𝐵 + 𝐶 ------- (3)

19. Put 𝐵 =
1
3
& 𝐶 = −
2
9
in (3)
⇒ 0 = −2𝐴 + 2
1
3
−
2
9
⇒ −2𝐴 +
2
3
−
2
9
= 0 ⇒ −2𝐴 =
2
9
−
2
3
= 2
1
9
−
1
3
=
2 1−3
9
=
2 −2
9
= −
4
9
⇒ 𝐴 =
2
9
(1) ⇒
𝑥
𝑥−1 2 𝑥+2
=
𝐴
𝑥−1
+
𝐵
𝑥−1 2 +
𝐶
𝑥+2
= −
2
9
1
𝑥−1
+
1
3
1
𝑥−1 2 −
2
9
1
𝑥+2
∴
𝑥 𝑑𝑥
𝑥−1 2 𝑥+2
=
2
9
𝑑𝑥
𝑥−1
+
1
3
𝑑𝑥
𝑥−1 2 −
2
9
𝑑𝑥
𝑥+2
=
2
9
log 𝑥 − 1 +
1
3
−
1
𝑥−1 −1 −
2
9
log 𝑥 + 2 + 𝐶 ,
(∵
𝑑𝑥
𝑎𝑥± 𝑏
=
1
𝑎
log 𝑎𝑥 ± 𝑏 + 𝐶 &
𝑑𝑥
𝑎𝑥±𝑏 𝑛 =
1
𝑎 −𝑛+1 𝑎𝑥±𝑏 −𝑛+1 + 𝐶 )
=
2
9
log 𝑥 − 1 −
1
3
𝑥 − 1 −
2
9
log 𝑥 + 2 + 𝐶
=
2
9
log 𝑥 − 1 + log 𝑥 + 2 −
1
3
𝑥 − 1 + 𝐶
=
2
9
log 𝑥 − 1 𝑥 + 2 −
𝑥−1
3
+ 𝐶

20. Problem 3: Evaluate
𝟏𝟎 𝒅𝒙
(𝒙−𝟏)(𝒙𝟐+𝟗)
Solution:
Consider
10
(𝑥−1)(𝑥2+9)
=
𝐴
𝑥−1
+
𝐵𝑥+𝐶
𝑥2+9
----- (1)
⇒ 10 = 𝐴 𝑥2
+ 9 + (𝑥 − 1)(𝐵𝑥 + 𝐶) ------ (2)
Put 𝑥 = 1 in (2)
⇒ 10 = 𝐴 12
+ 9 + (1 − 1)(𝐵 1 + 𝐶)
⇒ 10 = 𝐴 1 + 9 + (𝐵 + 𝐶)(0)
⇒ 10 = 𝐴 10 ⇒ 𝐴 =
10
10
= 1
Put 𝑥 = 0 in (2)
⇒ 10 = 𝐴 0 + 9 + 0 − 1 𝐵 0 + 𝐶
⇒ 9𝐴 − 𝐶 = 10 ----- (3)
Put 𝐴 = 1 in (3), 9 1 − 𝐶 = 10 ⇒ −𝐶 = 10 − 9 = 1 ⇒ 𝐶 = −1
Put 𝑥 = −1 in (2)
⇒ 10 = 𝐴 −1 2
+ 9 + (−1 − 1)(𝐵 −1 + 𝐶)
⇒ 10 = 𝐴 1 + 9 + (−2)(−𝐵 + 𝐶)
⇒ 10 = 10𝐴 − 2(−𝐵 + 𝐶) ----- (4)
Put 𝐴 = 1, 𝐶 = −1 in (4), ⇒ 10 = 10 1 − 2(−𝐵 − 1)
⇒ 10 = 10 + 2𝐵 + 2 ⇒ 2𝐵 = 10 − 10 − 2 = −2 ⇒ 𝐵 = −1
(1) ⇒
10
(𝑥−1)(𝑥2+9)
=
1
𝑥−1
+
−𝑥−1
𝑥2+9

21. 10 𝑑𝑥
(𝑥−1)(𝑥2+9)
=
𝑑𝑥
𝑥−1
+
−𝑥−1
𝑥2+9
𝑑𝑥
=
𝑑𝑥
𝑥−1
−
𝑥
𝑥2+9
𝑑𝑥 −
1
𝑥2+9
𝑑𝑥 ------ (5)
Consider
𝑥
𝑥2+9
𝑑𝑥
Here we take 𝑥2
+ 9 = 𝑡 ⇒ 2𝑥 𝑑𝑥 = 𝑑𝑡 ⇒ 𝑥𝑑𝑥 =
𝑑𝑡
2
𝑥
𝑥2+9
𝑑𝑥 =
𝑑𝑡
2𝑡
=
1
2
𝑑𝑡
𝑡
=
1
2
log 𝑡 =
1
2
log(𝑥2
+ 9) ---- (6)
Using (6) in (5)
10 𝑑𝑥
(𝑥−1)(𝑥2+9)
= log 𝑥 − 1 −
1
2
log 𝑥2
+ 9 −
1
3
tan−1 𝑥
3
+ 𝐶
(∵
𝑑𝑥
𝑎𝑥± 𝑏
=
1
𝑎
log 𝑎𝑥 ± 𝑏 + 𝐶 &
𝑑𝑥
𝑎2+𝑥2
=
1
𝑎
tan−1 𝑥
𝑎
+ 𝐶 )

22. Problem 4: Evaluate 𝟎
𝝅
𝟐
𝒄𝒐𝒔𝒙𝒔𝒊𝒏𝒙 𝒅𝒙
𝐜𝐨𝐬𝟐 𝒙+𝟑𝒄𝒐𝒔𝒙+𝟐
Solution:
Consider
𝑐𝑜𝑠𝑥 𝑠𝑖𝑛𝑥 𝑑𝑥
cos2 𝑥+3 cos 𝑥+2
Here we take cos 𝑥 = 𝑡 ⟹ −𝑠𝑖𝑛𝑥 𝑑𝑥 = 𝑑𝑡 ⇒ 𝑠𝑖𝑛𝑥 𝑑𝑥 = −𝑑𝑡
𝑐𝑜𝑠𝑥 𝑠𝑖𝑛𝑥 𝑑𝑥
cos2 𝑥+3 cos 𝑥+2
=
𝑡(−𝑑𝑡)
𝑡2+3𝑡+2
= −
𝑡𝑑𝑡
(𝑡+2)(𝑡+1)
------- (1)
Consider
𝑡
(𝑡+2)(𝑡+1)
=
𝐴
𝑡+2
+
𝐵
𝑡+1
------- (2)
𝑡 = 𝐴 𝑡 + 1 + 𝐵(𝑡 + 2) ------- (3)
Put 𝑡 = −1 in (3)
−1 = 𝐴 −1 + 1 + 𝐵 −1 + 2
⇒ −1 = 𝐴 0 + 𝐵(1)
⇒ 𝐵 = −1
Put 𝑡 = −2 in (3)
−2 = 𝐴(−2 + 1) + 𝐵(−2 + 2)
⇒ −2 = 𝐴 −1 + 𝐵 0
⇒ −𝐴 = −2 ⇒ 𝐴 = 2
(2) ⇒
𝑡
(𝑡+2)(𝑡+1)
=
2
𝑡+2
+
(−1)
𝑡+1
=
2
𝑡+2
−
1
𝑡+1
(1) ⇒
𝑐𝑜𝑠𝑥 𝑠𝑖𝑛𝑥 𝑑𝑥
cos2 𝑥+3 cos 𝑥+2
= −
𝑡𝑑𝑡
𝑡+2 𝑡+1
= −
2 𝑑𝑡
𝑡+2
−
𝑑𝑡
𝑡+1

23. = −
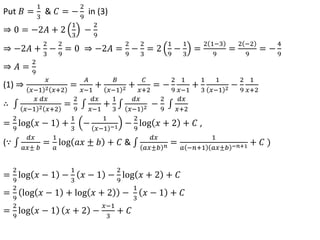
2 𝑑𝑡
𝑡+2
−
𝑑𝑡
𝑡+1
= −2
𝑑𝑡
𝑡+2
+
𝑑𝑡
𝑡+1
= −2 log 𝑡 + 2 + log(𝑡 + 1)
= −2 log 𝑐𝑜𝑠𝑥 + 2 + log(𝑐𝑜𝑠𝑥 + 1)
0
𝜋
2
𝑐𝑜𝑠𝑥 𝑠𝑖𝑛𝑥 𝑑𝑥
cos2 𝑥+3 cos 𝑥+2
= ]
−2 log 𝑐𝑜𝑠𝑥 + 2 + log 𝑐𝑜𝑠𝑥 + 1 0
𝜋
2
= −2 log cos
𝜋
2
+ 2 + log(cos
𝜋
2
+ 1) - (−2 log 𝑐𝑜𝑠0 + 2 + log 𝑐𝑜𝑠0 + 1 )
= −2𝑙𝑜𝑔2 + 𝑙𝑜𝑔1 + 2𝑙𝑜𝑔3 − 𝑙𝑜𝑔2 = −3𝑙𝑜𝑔2 + 2𝑙𝑜𝑔3
= log 2−3
+ 𝑙𝑜𝑔32
= log
1
23 + 𝑙𝑜𝑔9 = log
1
8
+ 𝑙𝑜𝑔9 = 𝑙𝑜𝑔1 − 𝑙𝑜𝑔8 + 𝑙𝑜𝑔9 = 𝑙𝑜𝑔9 − 𝑙𝑜𝑔8 = log
9
8
Problem 5: Evaluate
𝐬𝐞𝐜𝟐 𝒙 𝒅𝒙
𝐭𝐚𝐧𝟐 𝒙+𝟑𝒕𝒂𝒏𝒙+𝟐
Solution:
Here we take 𝑡𝑎𝑛𝑥 = 𝑡 ⇒ sec2
𝑥 𝑑𝑥 = 𝑑𝑡
sec2 𝑥 𝑑𝑥
tan2 𝑥+3𝑡𝑎𝑛𝑥+2
=
𝑑𝑡
𝑡2+3𝑡+2
=
𝑑𝑡
(𝑡+2)(𝑡+1)
------- (1)
Consider
1
(𝑡+2)(𝑡+1)
=
𝐴
𝑡+2
+
𝐵
𝑡+1
----- (2)
⇒ 1 = 𝐴 𝑡 + 1 + 𝐵(𝑡 + 2) ------ (3)
Put 𝑡 = −1 in (3)
1 = 𝐴 −1 + 1 + 𝐵(−1 + 2)
1 = 𝐴 0 + 𝐵 1 ⇒ 𝐵 = 1
Put 𝑡 = −2 in (3)
1 = 𝐴 −2 + 1 + 𝐵(−2 + 2)
1 = 𝐴 −1 + 𝐵 0 ⇒ 𝐴 = −1
(2) ⇒
1
(𝑡+2)(𝑡+1)
=
−1
𝑡+2
+
1
𝑡+1

24. (1) ⇒
sec2 𝑥 𝑑𝑥
tan2 𝑥+3𝑡𝑎𝑛𝑥+2
=
𝑑𝑡
(𝑡+2)(𝑡+1)
=
−𝑑𝑡
𝑡+2
+
𝑑𝑡
𝑡+1
= −
𝑑𝑡
𝑡+2
+
𝑑𝑡
𝑡+1
= − log 𝑡 + 2 + log 𝑡 + 1 + 𝐶
= − log 𝑡𝑎𝑛𝑥 + 2 + log 𝑡𝑎𝑛𝑥 + 1 + 𝐶

25. Type III.(Method 2)- Completing the Square: If any terms involve quadratics,
eliminate the linear term if needed by completing the square. (denominator is
of second degree and does not resolve into rational factors)
- Integration of the form
𝒅𝒙
𝒂𝒙𝟐+𝒃𝒙+𝒄
If the denominator is of second degree and does not resolve into rational factors.
Then change the denominator into complete square form, the integral reduces to
one of the following three forms
1.
𝑑𝑥
𝑥2+𝑎2 =
1
𝑎
tan−1 𝑥
𝑎
2.
𝑑𝑥
𝑥2−𝑎2 =
1
2𝑎
log
𝑥−𝑎
𝑥+𝑎
3.
𝑑𝑥
𝑎2−𝑥2 =
1
2𝑎
log
𝑎+𝑥
𝑎−𝑥

26. Producer to form completing the square:
Suppose given quadratic polynomial is 𝑎𝑥2
± 𝑏𝑥 + 𝑐
Step1: Take the coefficient ′𝑎′ of 𝑥2 outside → 𝑎 𝑥2 ±
𝑏
𝑎
𝑥 +
𝑐
𝑎
Step 2: multiply the numerator and denominator of the coefficient
𝑏
𝑎
of 𝑥 by ′2′
→ 𝑎 𝑥2
±
2𝑏
2𝑎
𝑥 +
𝑐
𝑎
= 𝑎 𝑥2
± 2𝑥
𝑏
2𝑎
+
𝑐
𝑎
Step 3:
Considering 𝑥 = 𝐴 &
𝑏
2𝑎
= 𝐵
Now 𝑎 𝑥2
± 2𝑥
𝑏
2𝑎
+
𝑐
𝑎
= 𝑎 𝐴2
± 2𝐴𝐵 +
𝑐
𝑎
= 𝑎 𝐴2 ± 2𝐴𝐵 + 𝐵2 − 𝐵2 +
𝑐
𝑎
( ∵by adding & subtracting 𝐵2 =
𝑏
2𝑎
2
)
Step 4:
𝑎 𝐴2
± 2𝐴𝐵 + 𝐵2
− 𝐵2
+
𝑐
𝑎
= 𝑎 [ 𝐴 ± 𝐵 2
−𝐵2
+
𝑐
𝑎
]
= 𝑎[ 𝐴 ± 𝐵 2
+
𝑐
𝑎
− 𝐵2
] , where 𝐴 = 𝑥 , 𝐵 =
𝑏
2𝑎

27. Note:
If the given polynomial is 𝑥2
± 𝑏𝑥 + 𝑐
1. Divide the coefficient 𝑏 of 𝑥 by 2 →
𝑏
2
2. Then write 𝑥 ±
𝑏
2
2
+ 𝑐 −
𝑏
2
2
Problem 1: Evaluate
𝒅𝒙
𝒙𝟐+𝟐𝒙+𝟓
Solution:
𝑑𝑥
𝑥2+2𝑥+5
=
𝑑𝑥
𝑥+1 2−12+5
=
𝑑𝑥
𝑥+1 2 −1+5
=
𝑑𝑥
𝑥+1 2+4
=
𝑑𝑥
𝑥+1 2+22 =
1
2
tan−1
(
𝑥+1
2
)
∵
𝑑𝑥
𝑥2+𝑎2 =
1
𝑎
tan−1 𝑥
𝑎
, ℎ𝑒𝑟𝑒 𝑥 → 𝑥 + 1 , 𝑎 → 2

28. Problem 2: Evaluate
𝒅𝒙
𝟒𝒙𝟐−𝟒𝒙+𝟐
Solution:
𝑑𝑥
4𝑥2−4𝑥+2
=
𝑑𝑥
4(𝑥2−𝑥+
2
4
)
=
1
4
𝑑𝑥
𝑥2 −𝑥+
1
2
=
1
4
𝑑𝑥
𝑥−
1
2
2
+
1
2
−
1
2
2
=
1
4
𝑑𝑥
𝑥−
1
2
2
+
1
2
−
1
4
=
1
4
𝑑𝑥
𝑥−
1
2
2
+
1
4
=
1
4
𝑑𝑥
𝑥−
1
2
2
+
1
2
2 =
1
4
[
1
1
2
tan−1
(
𝑥−
1
2
1
2
)]
=
1
4
[ 2 tan−1
((
2𝑥−1
2
)(
2
1
)) =
1
2
tan−1
(2𝑥 − 1)
∵
𝑑𝑥
𝑥2+𝑎2 =
1
𝑎
tan−1 𝑥
𝑎
, ℎ𝑒𝑟𝑒 𝑥 → 𝑥 −
1
2
, 𝑎 →
1
2
Problem 3: Evaluate
𝒅𝒙
𝒙𝟐+𝟖𝒙−𝟕
Solution:
𝑑𝑥
𝑥2+8𝑥−7
=
𝑑𝑥
𝑥+
8
2
2
−7−
8
2
2
=
𝑑𝑥
𝑥+4 2−7− 4 2
=
𝑑𝑥
𝑥+4 2−7−16
=
𝑑𝑥
𝑥+4 2−23

29. =
𝑑𝑥
𝑥+4 2− 23
2
=
1
2 23
log
𝑥+4− 23
𝑥+4+ 23
∵
𝑑𝑥
𝑥2−𝑎2 =
1
2𝑎
log
𝑥−𝑎
𝑥+𝑎
, ℎ𝑒𝑟𝑒 𝑥 → 𝑥 + 4 , 𝑎 → 23
Problem 4 : Evaluate
𝒅𝒙
𝟏−𝟔𝒙−𝟗𝒙𝟐
Solution:
𝑑𝑥
1−6𝑥−9𝑥2 =
𝑑𝑥
9(
1
9
−
6
9
𝑥−𝑥2)
=
1
9
𝑑𝑥
(
1
9
−(
2
3
𝑥+𝑥2)
=
1
9
𝑑𝑥
(
1
9
−(𝑥2+
2
3
𝑥)
=
1
9
𝑑𝑥
1
9
− 𝑥+
2
3
2
2
−
2
3
2
2 =
1
9
𝑑𝑥
1
9
− 𝑥+
2
3 2
2
+
2
3 2
2 =
1
9
𝑑𝑥
1
9
− 𝑥+
1
3
2
+
1
9
=
1
9
𝑑𝑥
2
9
− 𝑥+
1
3
2 =
1
9
𝑑𝑥
2
9
2
− 𝑥+
1
3
2
=
1
9
.
1
2.
2
9
log
2
9
+𝑥+
1
3
2
9
− 𝑥+
1
3
=
1
9
.
1
2.
2
3
log
(
2
3
+𝑥+
1
3
)
(
2
3
−𝑥−
1
3
)
=
1
6 2
log
2+3𝑥+1
2 −3𝑥−1
∵
𝑑𝑥
𝑎2−𝑥2 =
1
2𝑎
log
𝑎+𝑥
𝑎−𝑥
, ℎ𝑒𝑟𝑒 𝑥 → 𝑥 +
1
3
, 𝑎 →
2
9

30. Type IV-(Method 2). Integration of the form
𝒑𝒙+𝒒 𝒅𝒙
𝒂𝒙𝟐+𝒃𝒙+𝒄
Step 1.Put 𝑝𝑥 + 𝑞 = 𝐴
𝑑
𝑑𝑥
𝑎𝑥2 + 𝑏𝑥 + 𝑐 + 𝐵
Step 2. Find the value of A and B
Step 3. Then given integral becomes
𝑝𝑥+𝑞 𝑑𝑥
𝑎𝑥2+𝑏𝑥+𝑐
= 𝐴 log(𝑎𝑥2 + 𝑏𝑥 + 𝑐) +
𝐵
𝑑𝑥
𝑎𝑥2+𝑏𝑥+𝑐
Step 4. Substitute the values of A and B and use method 2(Type III) to solve 2nd
integration.

31. Problem 1 : Evaluate
𝟐𝒙+𝟑
𝒙𝟐+𝒙+𝟏
𝒅𝒙
Solution:
Let 2𝑥 + 3 = 𝐴
𝑑
𝑑𝑥
𝑥2
+ 𝑥 + 1 + 𝐵
⇒ 2𝑥 + 3 = 𝐴 2𝑥 + 1 + 𝐵
⇒ 2𝑥 + 3 = 2𝐴𝑥 + (𝐴 + 𝐵)
Comparing the coefficients of 𝑥 and constant terms on both sides
⇒ 𝐴 = 1 & 𝐴 + 𝐵 = 3
𝑃𝑢𝑡 𝐴 = 1 𝑖𝑛 𝐴 + 𝐵 = 3 ⇒ 1 + 𝐵 = 3 ⇒ 𝐵 = 3 − 1 = 2
2𝑥+3
𝑥2+𝑥+1
𝑑𝑥 = 𝐴 log 𝑥2
+ 𝑥 + 1 + 𝐵
𝑑𝑥
𝑥2+𝑥+1
= 1 . log 𝑥2
+ 𝑥 + 1 + 2
𝑑𝑥
𝑥2+𝑥+1
= log 𝑥2
+ 𝑥 + 1 + 2
𝑑𝑥
𝑥+
1
2
2
+1−
1
2
2
= log 𝑥2
+ 𝑥 + 1 + 2
𝑑𝑥
𝑥+
1
2
2
+1−
1
4
= log 𝑥2
+ 𝑥 + 1 + 2
𝑑𝑥
𝑥+
1
2
2
+
4−1
4
= log 𝑥2
+ 𝑥 + 1 + 2
𝑑𝑥
𝑥+
1
2
2
+
3
4
= log 𝑥2
+ 𝑥 + 1 + 2
𝑑𝑥
𝑥+
1
2
2
+
3
4
2

32. = log 𝑥2 + 𝑥 + 1 + 2
𝑑𝑥
𝑥+
1
2
2
+
3
4
2
= log 𝑥2
+ 𝑥 + 1 + 2
1
3
4
tan−1
𝑥+
1
2
3
4
∵
𝑑𝑥
𝑥2+𝑎2 =
1
𝑎
tan−1 𝑥
𝑎
, ℎ𝑒𝑟𝑒 𝑥 → 𝑥 +
1
2
, 𝑎 →
3
4
= log 𝑥2
+ 𝑥 + 1 + 2
1
3
2
tan−1
𝑥+
1
2
3
2
= log 𝑥2
+ 𝑥 + 1 + 2
2
3
tan−1
2𝑥+1
2
3
2
= log 𝑥2
+ 𝑥 + 1 +
4
3
tan−1 2𝑥+1
3

33. Problem 2: Evaluate 𝒙𝟐 + 𝟏 +
𝟏
𝒙𝟐+𝟏
𝒅𝒙
Solution:
𝑥2 + 1 +
1
𝑥2+1
𝑑𝑥 = 𝑥2𝑑𝑥 + 1. 𝑑𝑥 +
𝑑𝑥
1+𝑥2
=
𝑥3
3
+ 𝑥 + tan−1 𝑥
∵
𝑑𝑥
𝑎2+𝑥2 =
1
𝑎
tan−1 𝑥
𝑎
, ℎ𝑒𝑟𝑒 𝑎 → 1

34. Integration of irrational functions
Method 4. (Type I)-Integration of the form
𝒅𝒙
𝒂𝒙𝟐+𝒃𝒙+𝒄
Change the denominator into complete square form, the integral reduces to one of the following
three forms
1.
𝑑𝑥
𝑎2−𝑥2
= sin−1 𝑥
𝑎
2.
𝑑𝑥
𝑎2+𝑥2
= sinh−1
(
𝑥
𝑎
)
3.
𝑑𝑥
𝑥2−𝑎2
= cosh−1 𝑥
𝑎
Problem 1: Evaluate
𝒅𝒙
𝟐𝒙𝟐+𝟑𝒙+𝟒
Solution:
𝑑𝑥
2𝑥2+3𝑥+4
=
𝑑𝑥
2 𝑥2+
3
2
𝑥+
4
2
=
1
2
𝑑𝑥
𝑥+
3
2
2
2
+2−
3
2
2
2
=
1
2
𝑑𝑥
𝑥+
3
4
2
+2−
3
4
2
=
1
2
𝑑𝑥
𝑥+
3
4
2
+2−
9
16

35. =
1
2
𝑑𝑥
𝑥+
3
4
2
+
32−9
16
=
1
2
𝑑𝑥
𝑥+
3
4
2
+
23
16
=
1
2
𝑑𝑥
𝑥+
3
4
2
+
23
16
2
=
1
2
𝑑𝑥
𝑥+
3
4
2
+
23
4
2
=
1
2
𝑆𝑖𝑛ℎ−1
𝑥+
3
4
23
4
∵
𝑑𝑥
𝑥2+𝑎2
= 𝑆𝑖𝑛ℎ −1 𝑥
𝑎
, ℎ𝑒𝑟𝑒 𝑥 → 𝑥 +
3
4
, 𝑎 →
23
4
=
1
2
𝑆𝑖𝑛ℎ−1
4𝑥+3
4
23
4
=
1
2
𝑆𝑖𝑛ℎ−1 4𝑥+3
23

36. Problem 2: Evaluate
𝒅𝒙
𝟐−𝟑𝒙+𝒙𝟐
Solution:
𝑑𝑥
2−3𝑥+𝑥2
=
𝑑𝑥
𝑥2−3𝑥+2
=
𝑑𝑥
𝑥−
3
2
2
+2−
3
2
2
=
𝑑𝑥
𝑥−
3
2
2
+2 −
9
4
=
𝑑𝑥
𝑥−
3
2
2
+
8−9
4
=
𝑑𝑥
𝑥−
3
2
2
−
1
4
=
𝑑𝑥
𝑥−
3
2
2
−
1
2
2
= 𝐶𝑜𝑠ℎ−1
𝑥−
3
2
1
2
= 𝐶𝑜𝑠ℎ−1
2𝑥−3
2
1
2
= 𝐶𝑜𝑠ℎ−1 2𝑥−3
1
= 𝐶𝑜𝑠ℎ−1
2𝑥 − 3

37. Method 4.(Type II)- Integration of the form
(𝒑𝒙+𝒒)𝒅𝒙
𝒂𝒙𝟐+𝒃𝒙+𝒄
Step 1.Put 𝑝𝑥 + 𝑞 = 𝐴
𝑑
𝑑𝑥
𝑎𝑥2
+ 𝑏𝑥 + 𝑐 + 𝐵
Step 2. Find the value of A and B
Step 3. Then given integral becomes
𝑝𝑥+𝑞 𝑑𝑥
𝑎𝑥2+𝑏𝑥+𝑐
=
𝐴 𝑎𝑥2 + 𝑏𝑥 + 𝑐 + 𝐵
𝒅𝒙
𝒂𝒙𝟐+𝒃𝒙+𝒄
Step 4. Substitute the values of A and B and use method 4(Type I) to solve 2nd integration
Problem 1: Evaluate
𝒙+𝟏 𝒅𝒙
𝒙𝟐−𝒙+𝟏
Solution:
Let 𝑥 + 1 = 𝐴
𝑑
𝑑𝑥
𝑥2
− 𝑥 + 1 + 𝐵
= 𝐴 2𝑥 − 1 + 𝐵
𝑥 + 1 = 2𝐴𝑥 − 𝐴 + 𝐵
Comparing the coefficients of 𝑥 and constant terms on both sides
2𝐴 = 1 ⇒ 𝐴 =
1
2
−𝐴 + 𝐵 = 1
−
1
2
+ 𝐵 = 1 ⇒ 𝐵 = 1 +
1
2
=
3
2

38. 𝑥+1 𝑑𝑥
𝑥2−𝑥+1
= 𝐴 𝑥2 − 𝑥 + 1 + 𝐵
𝑑𝑥
𝑥2−𝑥+1
=
1
2
𝑥2 − 𝑥 + 1 +
3
2
𝑑𝑥
𝑥2−𝑥+1
=
1
2
𝑥2 − 𝑥 + 1 +
3
2
𝑑𝑥
𝑥−
1
2
2
+1−
1
2
2
=
1
2
𝑥2 − 𝑥 + 1 +
3
2
𝑑𝑥
𝑥−
1
2
2
+1−
1
4
=
1
2
𝑥2 − 𝑥 + 1 +
3
2
𝑑𝑥
𝑥−
1
2
2
+
4−1
4
=
1
2
𝑥2 − 𝑥 + 1 +
3
2
𝑑𝑥
𝑥−
1
2
2
+
3
4
=
1
2
𝑥2 − 𝑥 + 1 +
3
2
𝑑𝑥
𝑥−
1
2
2
+
3
4
2
=
1
2
𝑥2 − 𝑥 + 1 +
3
2
𝑑𝑥
𝑥−
1
2
2
+
3
2
2
=
1
2
𝑥2 − 𝑥 + 1 +
3
2
𝑆𝑖𝑛ℎ−1
𝑥−
1
2
3
2
∵
𝑑𝑥
𝑥2+𝑎2
= 𝑆𝑖𝑛ℎ−1 𝑥
𝑎
, ℎ𝑒𝑟𝑒 𝑥 → 𝑥 −
1
2
, 𝑎 →
3
2
=
1
2
𝑥2 − 𝑥 + 1 +
3
2
𝑆𝑖𝑛ℎ−1
2𝑥−1
2
3
2
=
1
2
𝑥2 − 𝑥 + 1 +
3
2
𝑆𝑖𝑛ℎ−1 2𝑥−1
3

39. Problem 2: Evaluate
𝒙 𝒅𝒙
𝒙𝟐+𝒙+𝟏
Solution:
Let 𝑥 = 𝐴
𝑑
𝑑𝑥
𝑥2
+ 𝑥 + 1 + 𝐵
= 𝐴 2𝑥 + 1 + 𝐵
𝑥 = 2𝐴𝑥 + 𝐴 + 𝐵
Comparing the coefficients of 𝑥 and constant terms on both sides
2𝐴 = 1 ⇒ 𝐴 =
1
2
𝐴 + 𝐵 = 1
1
2
+ 𝐵 = 1 ⇒ 𝐵 = 1 −
1
2
=
1
2
𝑥𝑑𝑥
𝑥2+𝑥+1
= 𝐴 𝑥2 + 𝑥 + 1 + 𝐵
𝑑𝑥
𝑥2+𝑥+1
=
1
2
𝑥2 + 𝑥 + 1 +
1
2
𝑑𝑥
𝑥2+𝑥+1
=
1
2
𝑥2 + 𝑥 + 1 +
1
2
𝑑𝑥
𝑥+
1
2
2
+1−
1
2
2
=
1
2
𝑥2 + 𝑥 + 1 +
1
2
𝑑𝑥
𝑥+
1
2
2
+1−
1
4
=
1
2
𝑥2 + 𝑥 + 1 +
1
2
𝑑𝑥
𝑥+
1
2
2
+
4−1
4

40. =
1
2
𝑥2 + 𝑥 + 1 +
1
2
𝑑𝑥
𝑥+
1
2
2
+
3
4
=
1
2
𝑥2 + 𝑥 + 1 +
1
2
𝑑𝑥
𝑥+
1
2
2
+
3
4
2
=
1
2
𝑥2 + 𝑥 + 1 +
1
2
𝑑𝑥
𝑥+
1
2
2
+
3
2
2
=
1
2
𝑥2 + 𝑥 + 1 +
1
2
𝑆𝑖𝑛ℎ−1
𝑥+
1
2
3
2
∵
𝑑𝑥
𝑥2+𝑎2
= 𝑆𝑖𝑛ℎ−1 𝑥
𝑎
, ℎ𝑒𝑟𝑒 𝑥 → 𝑥 +
1
2
, 𝑎 →
3
2
=
1
2
𝑥2 + 𝑥 + 1 +
1
2
𝑆𝑖𝑛ℎ−1
2𝑥+1
2
3
2
=
1
2
𝑥2 + 𝑥 + 1 +
1
2
𝑆𝑖𝑛ℎ−1 2𝑥+1
3

41. Problem 3: Evaluate
𝟐𝒙+𝟓 𝒅𝒙
𝒙𝟐−𝟐𝒙+𝟏𝟎
Solution:
Let 2𝑥 + 5 = 𝐴
𝑑
𝑑𝑥
𝑥2
− 2𝑥 + 10 + 𝐵
= 𝐴 2𝑥 − 2 + 𝐵
2𝑥 + 5 = 2𝐴𝑥 − 2𝐴 + 𝐵
Comparing the coefficients of 𝑥 and constant terms on both sides
2𝐴 = 2 ⇒ 𝐴 =
2
2
= 1
−2𝐴 + 𝐵 = 5
−2 1 + 𝐵 = 5 ⇒ 𝐵 = 5 + 2 = 7
2𝑥+5 𝑑𝑥
𝑥2−2𝑥+10
= 𝐴 𝑥2 − 2𝑥 + 10 + 𝐵
𝑑𝑥
𝑥2−2𝑥+10
= 1. 𝑥2 − 2𝑥 + 10 + 7
𝑑𝑥
𝑥2−2𝑥+10
= 𝑥2 − 2𝑥 + 10 + 7
𝑑𝑥
𝑥−
2
2
2
+10−
2
2
2
= 𝑥2 − 2𝑥 + 10 + 7
𝑑𝑥
𝑥−1 2+10−1
= 𝑥2 − 2𝑥 + 10 + 7
𝑑𝑥
𝑥−1 2+9

42. = 𝑥2 − 2𝑥 + 10 + 7
𝑑𝑥
𝑥−1 2+32
= 𝑥2 − 2𝑥 + 10 + 7 𝑆𝑖𝑛ℎ−1 𝑥−1
3
∵
𝑑𝑥
𝑥2+𝑎2
= 𝑆𝑖𝑛ℎ−1 𝑥
𝑎
, ℎ𝑒𝑟𝑒 𝑥 → 𝑥 − 1 , 𝑎 → 3
Problem 4: Evaluate
𝟓−𝒙
𝟐−𝒙
𝒅𝒙
Solution:
Hint:
5−𝑥
2−𝑥
𝑑𝑥 =
5−𝑥
2−𝑥
𝑑𝑥 =
5−𝑥
2−𝑥
5−𝑥
5−𝑥
𝑑𝑥
=
5−𝑥
(2−𝑥)(5−𝑥)
𝑑𝑥
=
5−𝑥 𝑑𝑥
−10+7𝑥−𝑥2
, then use method 4 (Type II)

43. Method 4.(Type III)- Integration of the form 𝒂𝒙𝟐 + 𝒃𝒙 + 𝒄 𝒅𝒙
Change the function inside the square root into complete square form, the integral
reduces to one of the following three forms
1. 𝑎2 − 𝑥2 𝑑𝑥 =
1
2
𝑥 𝑎2 − 𝑥2 +
1
2
𝑎2 sin−1 𝑥
𝑎
2. 𝑥2 + 𝑎2 𝑑𝑥 =
1
2
𝑥 𝑥2 + 𝑎2 +
1
2
𝑎2 sinh−1 𝑥
𝑎
3. 𝑥2 − 𝑎2 𝑑𝑥 =
1
2
𝑥 𝑥2 − 𝑎2 −
1
2
𝑎2
cosh−1 𝑥
𝑎
Problem 1: Evaluate 𝒙𝟐 + 𝟐𝒙 + 𝟏𝟎 𝒅𝒙
Solution:
𝑥2 + 2𝑥 + 10 𝑑𝑥 = 𝑥 +
2
2
2
+ 10 −
2
2
2
𝑑𝑥
= 𝑥 + 1 2 + 10 − 1 𝑑𝑥
= 𝑥 + 1 2 + 9 𝑑𝑥 = 𝑥 + 1 2 + 32 𝑑𝑥
=
1
2
𝑥 + 1 𝑥 + 1 2 + 9 +
1
2
3 2 𝑆𝑖𝑛ℎ−1 𝑥+1
3
(∵ 𝑥2 + 𝑎2 𝑑𝑥 =
1
2
𝑥 𝑥2 + 𝑎2 +
1
2
𝑎2 sinh−1 𝑥
𝑎
, ℎ𝑒𝑟𝑒 𝑥 → 𝑥 + 1 , 𝑎 → 3)

44. Method 4.(Type IV)- Integration of the form (𝒑𝒙 + 𝒒) 𝒂𝒙𝟐 + 𝒃𝒙 + 𝒄 𝒅𝒙
Step 1.Put 𝑝𝑥 + 𝑞 = 𝐴
𝑑
𝑑𝑥
𝑎𝑥2
+ 𝑏𝑥 + 𝑐 + 𝐵
Step 2. Find the value of A and B
Step 3. Then given integral becomes (𝒑𝒙 + 𝒒) 𝒂𝒙𝟐 + 𝒃𝒙 + 𝒄 𝒅𝒙 =
= 𝐴
2
3
𝑎𝑥2 + 𝑏𝑥 + 𝑐
3
2 + 𝐵 𝒂𝒙𝟐 + 𝒃𝒙 + 𝒄 𝒅𝒙
Step 4. Substitute the values of A and B and solve by using method 4 (Type III).
Problem 1: Evaluate 𝟑𝒙 − 𝟐 𝒙𝟐 + 𝒙 + 𝟏 𝒅𝒙
Solution:
Let 3𝑥 − 2 = 𝐴
𝑑
𝑑𝑥
𝑥2
+ 𝑥 + 1 + 𝐵
3𝑥 − 2 = 𝐴 2𝑥 + 1 + 𝐵
3𝑥 − 2 = 2𝐴𝑥 + 𝐴 + 𝐵
Comparing the coefficients of 𝑥 and constant terms on both sides
2𝐴 = 3 ⇒ 𝐴 =
3
2
𝐴 + 𝐵 = −2 ⇒
3
2
+ 𝐵 = −2
𝐵 = −2 −
3
2
= −
7
2

45. 3𝑥 − 2 𝑥2 + 𝑥 + 1 𝑑𝑥 = 𝐴
2
3
𝑥2 + 𝑥 + 1
3
2 + 𝐵 𝑥2 + 𝑥 + 1 𝑑𝑥
=
3
2
2
3
𝑥2 + 𝑥 + 1
3
2 −
7
2
𝑥2 + 𝑥 + 1 𝑑𝑥
= 𝑥2
+ 𝑥 + 1
3
2 −
7
2
𝑥 +
1
2
2
+ 1 −
1
2
2
𝑑𝑥
= 𝑥2
+ 𝑥 + 1
3
2 −
7
2
𝑥 +
1
2
2
+ 1 −
1
4
𝑑𝑥
= 𝑥2
+ 𝑥 + 1
3
2 −
7
2
𝑥 +
1
2
2
+
4−1
4
𝑑𝑥
= 𝑥2 + 𝑥 + 1
3
2 −
7
2
𝑥 +
1
2
2
+
3
4
𝑑𝑥
= 𝑥2
+ 𝑥 + 1
3
2 −
7
2
𝑥 +
1
2
2
+
3
4
2
𝑑𝑥

46. = 𝑥2 + 𝑥 + 1
3
2 −
7
2
𝑥 +
1
2
2
+
3
2
2
𝑑𝑥
= 𝑥2
+ 𝑥 + 1
3
2 −
7
2
1
2
𝑥 +
1
2
𝑥 +
1
2
2
+
3
2
+
1
2
3
2
2
𝑆𝑖𝑛ℎ−1
𝑥+
1
2
3
2
(∵ 𝑥2 + 𝑎2 𝑑𝑥 =
1
2
𝑥 𝑥2 + 𝑎2 +
1
2
𝑎2 sinh−1 𝑥
𝑎
, ℎ𝑒𝑟𝑒 𝑥 → 𝑥 +
1
2
, 𝑎 →
3
2
)
= 𝑥2 + 𝑥 + 1
3
2 −
7
2
1
2
2𝑥+1
2
𝑥 +
1
2
2
+
3
4
+
1
2
3
4
𝑆𝑖𝑛ℎ−1
2𝑥+1
2
3
2
= 𝑥2 + 𝑥 + 1
3
2 −
7
2
1
2
2𝑥+1
2
𝑥 +
1
2
2
+
3
4
+
1
2
3
4
𝑆𝑖𝑛ℎ−1
2𝑥+1
2
3
2
= 𝑥2
+ 𝑥 + 1
3
2 −
7
8
2𝑥 + 1 𝑥 +
1
2
2
+
3
4
−
21
16
𝑆𝑖𝑛ℎ−1 2𝑥+1
3
= 𝑥2
+ 𝑥 + 1
3
2 −
7
8
2𝑥 + 1 𝑥2 + 2𝑥 + 1 −
21
16
𝑆𝑖𝑛ℎ−1 2𝑥+1
3

47. Method 4.(Type- IV)- Integration of the form
𝒅𝒙
𝒑𝒙+𝒒 𝒂𝒙𝟐+𝒃𝒙+𝒄
Step 1. Put 𝑝𝑥 + 𝑞 =
1
𝑡
Step 2. Then the given integration reduced to previous method and solve
Problem 1: Evaluate
𝒅𝒙
(𝒙+𝟏) 𝒙𝟐+𝒙+𝟏
Solution:
Let 𝑥 + 1 =
1
𝑡
⟹ 𝑑𝑥 = −
1
𝑡2 𝑑𝑡 & 𝑥 =
1
𝑡
− 1
𝑑𝑥
(𝑥+1) 𝑥2+𝑥+1
=
−
1
𝑡2𝑑𝑡
1
𝑡
1
𝑡
−1
2
+
1
𝑡
−1 +1
= −
𝑑𝑡
𝑡2
𝑡
1
𝑡
2
−
2
𝑡
+1+
1
𝑡
−1+1
= −
𝑑𝑡
𝑡
1
𝑡2+
1−2
𝑡
+1
= −
𝑑𝑡
𝑡
1
𝑡2−
1
𝑡
+1
= −
𝑑𝑡
𝑡
1−𝑡+𝑡2
𝑡2
= −
𝑑𝑡
𝑡
1−𝑡+𝑡2
𝑡
= −
𝑑𝑡
𝑡2−𝑡+1

48. = −
𝑑𝑡
𝑡−
1
2
2
+1−
1
2
2
= −
𝑑𝑡
𝑡−
1
2
2
+1−
1
4
= −
𝑑𝑡
𝑡−
1
2
2
+
4−1
4
= −
𝑑𝑡
𝑡−
1
2
2
+
3
4
= −
𝑑𝑡
𝑡−
1
2
2
+
3
4
2
= −
𝑑𝑡
𝑡−
1
2
2
+
3
2
2
= −𝑆𝑖𝑛ℎ−1
𝑡−
1
2
3
2
∵
𝑑𝑥
𝑥2+𝑎2
= 𝑆𝑖𝑛ℎ−1 𝑥
𝑎
, ℎ𝑒𝑟𝑒 𝑥 → 𝑡 −
1
2
, 𝑎 →
3
2
= −𝑆𝑖𝑛ℎ−1
1
𝑥+1
−
1
2
3
2
∵ 𝑥 + 1 =
1
𝑡
⇒ 𝑡 =
1
𝑥+1

49. = −𝑆𝑖𝑛ℎ−1
2− 𝑥+1
2 𝑥+1
3
2
= −𝑆𝑖𝑛ℎ−1 2−𝑥−1
3(𝑥+1)
= −𝑆𝑖𝑛ℎ−1 1−𝑥
3(𝑥+1)
Problem 2: Evaluate
𝒅𝒙
(𝒙+𝟏) 𝟐𝒙𝟐+𝟑𝒙+𝟒
Solution:
Let 𝑥 + 1 =
1
𝑡
⟹ 𝑑𝑥 = −
1
𝑡2 𝑑𝑡 & 𝑥 =
1
𝑡
− 1
𝑑𝑥
(𝑥+1) 2𝑥2+3𝑥+4
=
−
1
𝑡2𝑑𝑡
1
𝑡
2
1
𝑡
−1
2
+3
1
𝑡
−1 +4
=
−
1
𝑡2𝑑𝑡
2
𝑡
1
𝑡
−1
2
+
3
2
1
𝑡
−1 +
4
2
= −
𝑑𝑡
𝑡2 2
𝑡
1
𝑡
2
−
2
𝑡
+1+
3
2𝑡
−
3
2
+2

50. = −
𝑑𝑡
𝑡 2
1
𝑡
2
−
2
𝑡
+
3
2𝑡
+3−
3
2
+2
= −
1
2
𝑑𝑡
𝑡
1
𝑡
2
+
3−4
2𝑡
+5−
3
2
= −
1
2
𝑑𝑡
𝑡
1
𝑡2 −
1
2𝑡
+
6−3
2
= −
1
2
𝑑𝑡
𝑡
1
𝑡2−
1
2𝑡
+
3
2
= −
1
2
𝑑𝑡
𝑡
2−𝑡+3𝑡2
2𝑡2
= −
1
2
𝑑𝑡
𝑡
2−𝑡+3𝑡2
2𝑡
= −
𝑑𝑡
3𝑡2−𝑡+2

51. = −
𝑑𝑡
3 𝑡2−
𝑡
3
+
2
3
= −
1
3
𝑑𝑡
𝑡−
1
6
2
+
2
3
−
1
6
2
= −
1
3
𝑑𝑡
𝑡−
1
6
2
+
2
3
−
1
36
= −
1
3
𝑑𝑡
𝑡−
1
6
2
+
(12−1)
36
= −
1
3
𝑑𝑡
𝑡−
1
6
2
+
11
36
= −
1
3
𝑑𝑡
𝑡−
1
6
2
+
11
36
2
= −
1
3
𝑑𝑡
𝑡−
1
6
2
+
11
6
2
= −
1
3
𝑆𝑖𝑛ℎ−1
𝑡−
1
6
11
6
∵
𝑑𝑥
𝑥2+𝑎2
= 𝑆𝑖𝑛ℎ−1 𝑥
𝑎
, ℎ𝑒𝑟𝑒 𝑥 → 𝑡 −
1
6
, 𝑎 →
11
6
= −
1
3
𝑆𝑖𝑛ℎ−1
1
𝑥+1
−
1
6
11
6
∵ 𝑥 + 1 =
1
𝑡
⇒ 𝑡 =
1
𝑥+1

52. = −
1
3
𝑆𝑖𝑛ℎ−1
1
𝑥+1
−
1
6
11
6
= −
1
3
𝑆𝑖𝑛ℎ−1
6− 𝑥+1
6 𝑥+1
11
6
= −
1
3
𝑆𝑖𝑛ℎ−1 6−𝑥−1
11 (𝑥+1)
= −
1
3
𝑆𝑖𝑛ℎ−1 5−𝑥
11 (𝑥+1)
Problem 3: Evaluate
𝒅𝒙
(𝟑+𝒙) 𝒙
Solution:
Hint: Let 3 + 𝑥 =
1
𝑡

53. Method 5: Integral of the form
𝒔𝒊𝒏𝒎𝒙𝒄𝒐𝒔𝒏𝒙 𝒅𝒙 (or) 𝒔𝒊𝒏𝒎𝒙𝒔𝒊𝒏𝒏𝒙 𝒅𝒙 (or) 𝒄𝒐𝒔𝒎𝒙𝒄𝒐𝒔𝒏𝒙𝒅𝒙
1. 𝑠𝑖𝑛𝑚𝑥𝑐𝑜𝑠𝑛𝑥 𝑑𝑥 = −
cos 𝑚+𝑛 𝑥
2 𝑚+𝑛
−
cos 𝑚−𝑛 𝑥
2 𝑚−𝑛
+ 𝐶
2. 𝑠𝑖𝑛𝑚𝑥𝑠𝑖𝑛𝑛𝑥 𝑑𝑥 = −
sin 𝑚+𝑛 𝑥
2 𝑚+𝑛
−
sin 𝑚−𝑛 𝑥
2 𝑚−𝑛
+ 𝐶
3. 𝑐𝑜𝑠𝑚𝑥𝑐𝑜𝑠𝑛𝑥 𝑑𝑥 =
sin 𝑚+𝑛 𝑥
2 𝑚+𝑛
+
sin 𝑚−𝑛 𝑥
2 𝑚−𝑛
+ 𝐶
Problem 1: Find 𝒔𝒊𝒏𝟓𝜽𝒄𝒐𝒔𝟐𝜽𝒅𝜽
Solution:
Wkt 𝑠𝑖𝑛𝑚𝑥𝑐𝑜𝑠𝑛𝑥 𝑑𝑥 = −
cos 𝑚+𝑛 𝑥
2 𝑚+𝑛
−
cos 𝑚−𝑛 𝑥
2 𝑚−𝑛
+ 𝐶
Here 𝑚 = 5, 𝑛 = 2
𝑠𝑖𝑛5𝜃𝑐𝑜𝑠2𝜃𝑑𝜃 = −
cos 5+2 𝑥
2 5+2
−
cos 5−2 𝑥
2 5−2
+ 𝐶
= −
cos 7 𝑥
2 7
−
cos 3 𝑥
2 3
+ 𝐶
= −
cos 7 𝑥
14
−
cos 3 𝑥
6
+ 𝐶

54. Problem 2: Find 𝒔𝒊𝒏𝟕𝒙𝒔𝒊𝒏𝟒𝒙𝒅𝒙
Solution:
Wkt 𝑠𝑖𝑛𝑚𝑥𝑠𝑖𝑛𝑛𝑥 𝑑𝑥 = −
sin 𝑚+𝑛 𝑥
2 𝑚+𝑛
−
sin 𝑚−𝑛 𝑥
2 𝑚−𝑛
+ 𝐶
Here 𝑚 = 7, 𝑛 = 4
𝑠𝑖𝑛7𝑥𝑠𝑖𝑛4𝑥 𝑑𝑥 = −
sin 7+4 𝑥
2 7+4
−
sin 7−4 𝑥
2 7−4
+ 𝐶
= −
sin 11 𝑥
2 11
−
sin 3 𝑥
2 3
+ 𝐶
= −
sin 11 𝑥
22
−
sin 3 𝑥
6
+ 𝐶
Problem 3: Find 𝒄𝒐𝒔𝟒𝒙 𝒄𝒐𝒔𝟑𝒙𝒅𝒙
Solution:
Wkt 𝑐𝑜𝑠𝑚𝑥𝑐𝑜𝑠𝑛𝑥 𝑑𝑥 =
sin 𝑚+𝑛 𝑥
2 𝑚+𝑛
+
sin 𝑚−𝑛 𝑥
2 𝑚−𝑛
+ 𝐶
Here 𝑚 = 4, 𝑛 = 3
𝑐𝑜𝑠4𝑥𝑐𝑜𝑠3𝑥 𝑑𝑥 =
sin 4+3 𝑥
2 4+3
+
sin 4−3 𝑥
2 4−3
+ 𝐶
=
sin 7 𝑥
14
+
sin 𝑥
2
+ 𝐶

55. Formulas :
1.
2.
3.
4.
5.
6.
7.

56. 8.
9.
10.
11.
12.
13.
14.
15.

57. 16.
17.
18.
19.
20.
21.
22.
23.

58. 24.
25.
26.
27.
28.
29.
30.
31.

59. 32.
33.
34.
35.
36.
37.
38.

60. 39.
40.
41.
42.
43.
44.
45.
46.
47.

61. 48.
49.
50.
51.
52.
53.
54.
55.
56.

62. 57.

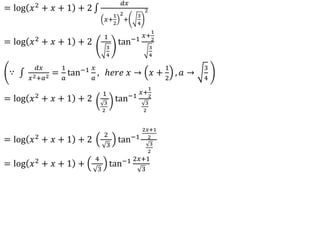
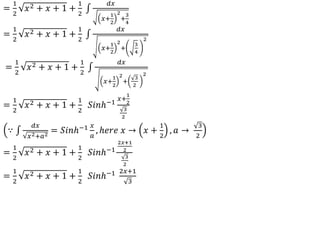
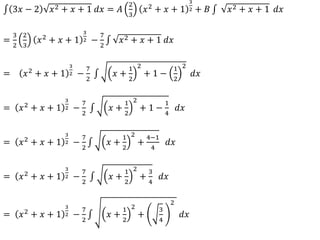
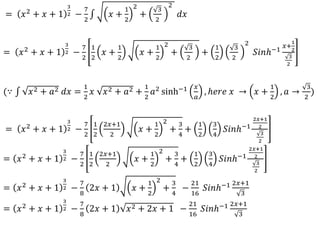
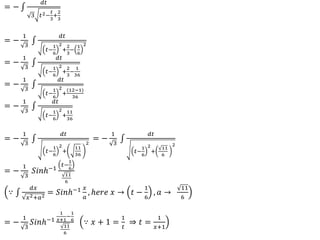
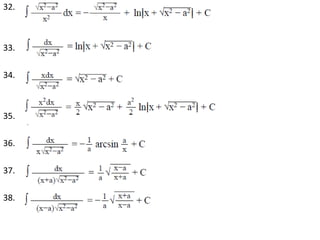
63. Definite Integrals
Suppose 𝑓(𝑥) is a continuous function defined in the interval [𝑎, 𝑏], divide the interval into
𝑛 subinterval with equal width Δ𝑥 and choose a point 𝑥𝑖 from each subinterval , then the
definite integral of 𝑓(𝑥) from 𝑎 to 𝑏 is
lim
𝑛→∞ 𝑖=1
𝑛
𝑓 𝑥𝑖 Δ𝑥 = 𝑎
𝑏
𝑓 𝑥 𝑑𝑥
If 𝑎
𝑏
𝑓 𝑥 𝑑𝑥 = ]
𝜙 𝑥 𝑎
𝑏
= 𝜙 𝑏 − 𝜙(𝑎)
Here, a is called the lower limit and b is called the upper limit of the definite integral
𝑎
𝑏
𝑓 𝑥 𝑑𝑥
Problem 1: Evaluate 𝟏
𝟐
𝒙𝟐
− 𝟑 𝒙 +
𝟏
𝒙𝟐 𝒅𝒙
Solution:
1
2
𝑥2
− 3 𝑥 +
1
𝑥2 𝑑𝑥
= 1
2
𝑥2
− 3𝑥
1
2 + 𝑥−2
𝑑𝑥
=
𝑥3
3
− 3
𝑥
1
2
+1
1
2
+1
+
𝑥−2+1
−2+1
1
2
=
𝑥3
3
− 3
𝑥
3
2
3
2
+
𝑥−1
−1
1
2
=
𝑥3
3
− 2𝑥
3
2 −
1
𝑥
1
2

64. = (
23
3
− 2(2
3
2) −
1
2
) − (
13
3
− 2 1
3
2 −
1
1
)
=
8
3
− 21+
3
2 −
1
2
−
1
3
+ 2 + 1
=
7
3
−
1
2
+ 3 − 2
5
2
=
14−3+18
6
− 2
5
2 =
29
6
− 2
5
2
Problem 2: Evaluate 𝟏
𝟐 𝒅𝒙
𝟑−𝟓𝒙 𝟐
Solution:
Consider
𝑑𝑥
3−5𝑥 2
Let 𝑡 = 3 − 5𝑥 ⇒ 𝑑𝑡 = −5𝑑𝑥 ⇒ 𝑑𝑥 = −
𝑑𝑡
5
𝑑𝑥
3−5𝑥 2 =
−
𝑑𝑡
5
𝑡2
= −
1
5
𝑑𝑡
𝑡2 = −
1
5
𝑡−2
𝑑𝑡 = −
1
5
𝑡−2+1
−2+1
= −
1
5
𝑡−1
−1
=
1
5𝑡
=
1
5 3+5𝑥
1
2 𝑑𝑥
3−5𝑥 2 =
1
5 3+5𝑥 1
2
=
1
5
1
3+5 2
−
1
3+5 1
=
1
5
1
13
−
1
8
=
8−13
(5)13 8
= −
5
5 104
= −
1
104

65. Problem 3: Calculate 𝒂
𝒃
𝒙 𝒅𝒙
Solution:
𝑎
𝑏
𝑥 𝑑𝑥 =
𝑥2
2 𝑎
𝑏
=
𝑏2
2
−
𝑎2
2
=
𝑏2−𝑎2
2
Problem 4: Evaluate 𝟎
𝝅
𝟐 𝒔𝒊𝒏𝒙 𝒅𝒙
Solution:
0
𝜋
2 𝑠𝑖𝑛𝑥 𝑑𝑥 = ]
−𝑐𝑜𝑠𝑥 0
𝜋
2
= − cos
𝜋
2
− − cos 0
= 0 + 1 = 1, (∵ 𝐶𝑜𝑠
𝜋
2
= 0 & 𝐶𝑜𝑠 0 = 1)
Problem 5: Evaluate 𝟎
𝟏 𝒅𝒙
𝟏+𝒙𝟐
Solution:
0
1 𝑑𝑥
1+𝑥2 = ]
tan−1
𝑥 0
1
∵
𝑑𝑥
𝑎2+𝑥2 =
1
𝑎
tan−1 𝑥
𝑎
, ℎ𝑒𝑟𝑒 𝑎 = 1
= tan−1
1 − tan−1
0
=
𝜋
4
− 0 =
𝜋
4
, (∵ tan−1 1 =
𝜋
4
& tan−1 0 = 0 )

66. Properties of Definite Integrals
1. 𝑎
𝑏
[ƒ(𝑥) + 𝑔(𝑥)] 𝑑𝑥 = 𝑎
𝑏
ƒ(𝑥) 𝑑𝑥 + 𝑎
𝑏
𝑔(𝑥) 𝑑𝑥
2. 𝑎
𝑏
𝑘ƒ(𝑥) 𝑑𝑥 = 𝑘 𝑎
𝑏
ƒ(𝑥) 𝑑𝑥
3. 𝑎
𝑎
ƒ(𝑥) 𝑑𝑥 = 0
4. 𝑎
𝑏
ƒ(𝑥) 𝑑𝑥 = − 𝑏
𝑎
ƒ(𝑥) 𝑑𝑥
5. 𝑎
𝑏
ƒ(𝑥) 𝑑𝑥 + 𝑏
𝑐
ƒ(𝑥) 𝑑𝑥 = 𝑎
𝑐
ƒ(𝑥) 𝑑𝑥, where 𝑎 < 𝑐 < 𝑏
6. a
b
f x dx = a
b
f z dz = a
b
f t dt
(The definite integral is independent of variable used.)
7. 0
𝑎
𝑓 𝑥 𝑑𝑥 = 0
𝑎
𝑓 𝑎 − 𝑥 𝑑𝑥
8.
−𝑎
𝑎
𝑓 𝑥 𝑑𝑥 =
0 , 𝑖𝑓 𝑓 𝑥 𝑖𝑠 𝑎𝑛 𝑜𝑑𝑑 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛, 𝑖. 𝑒 𝑓 −𝑥 = −𝑓(𝑥)
2 0
𝑎
𝑓 𝑥 𝑑𝑥, 𝑖𝑓 𝑓 𝑥 𝑖𝑠 𝑎𝑛 𝑒𝑣𝑒𝑛 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛, 𝑖. 𝑒 𝑓 −𝑥 = (𝑓(𝑥)
9. 0
𝑛𝑎
𝑓 𝑥 𝑑𝑥 = 𝑛 0
𝑎
𝑓 𝑥 𝑑𝑥 , 𝑖𝑓 𝑓 𝑎 + 𝑥 = 𝑓 𝑥
10. 0
𝑎
𝑓 𝑥 𝑑𝑥 =
0, 𝑖𝑓 𝑓 𝑎 − 𝑥 = −𝑓(𝑥)
2 0
𝑎
2 𝑓 𝑥 𝑑𝑥, 𝑖𝑓 𝑓 𝑎 − 𝑥 = 𝑓(𝑥)

67. Problem 1: Prove that 𝟎
𝝅
𝟐 𝐬𝐢𝐧𝒏
𝒙 𝒅𝒙 = 𝟎
𝝅
𝟐 𝐜𝐨𝐬𝒏
𝒙 𝒅𝒙
Solution:
Let 𝑓 𝑥 = 𝑆𝑖𝑛𝑛
𝑥 and 𝑎 =
𝜋
2
Wkt by the property(8) of definite integral 0
𝑎
𝑓 𝑥 𝑑𝑥 = 0
𝑎
𝑓 𝑎 − 𝑥 𝑑𝑥
0
𝜋
2 sin𝑛
𝑥 𝑑𝑥 = 0
𝜋
2 sin𝑛 𝜋
2
− 𝑥 𝑑𝑥 = 0
𝜋
2 cos𝑛
𝑥 𝑑𝑥
∵ sin
𝜋
2
− 𝑥 = 𝑐𝑜𝑠𝑥
Problem 2: Evaluate 𝟎
𝝅
𝟐
𝒔𝒊𝒏𝒙
𝟑
𝟐
𝒔𝒊𝒏𝒙
𝟑
𝟐+ 𝒄𝒐𝒔𝒙
𝟑
𝟐
𝒅𝒙
Solution:
Wkt by the property(8) of definite integral 0
𝑎
𝑓 𝑥 𝑑𝑥 = 0
𝑎
𝑓 𝑎 − 𝑥 𝑑𝑥 -----(1)
Let 𝑓 𝑥 =
𝑠𝑖𝑛𝑥
3
2
𝑠𝑖𝑛𝑥
3
2+ 𝑐𝑜𝑠𝑥
3
2
& 𝑎 =
𝜋
2
⇒ 𝑓 𝑎 − 𝑥 = 𝑓(
𝜋
2
− 𝑥) =
sin
𝜋
2
−𝑥
3
2
sin
𝜋
2
−𝑥
3
2
+ cos
𝜋
2
−𝑥
3
2
⇒ 𝑓
𝜋
2
− 𝑥 =
𝑐𝑜𝑠𝑥
3
2
𝑐𝑜𝑠𝑥
3
2+ 𝑠𝑖𝑛𝑥
3
2
, ∵ sin
𝜋
2
− 𝑥 = 𝑐𝑜𝑠𝑥 & cos
𝜋
2
− 𝑥 = 𝑠𝑖𝑛𝑥
And let I = 0
𝜋
2 𝑓 𝑥 𝑑𝑥 = 0
𝜋
2
𝑠𝑖𝑛𝑥
3
2
𝑠𝑖𝑛𝑥
3
2+ 𝑐𝑜𝑠𝑥
3
2
𝑑𝑥 -------- (2)

68. From (1) & (2)
𝐼 = 0
𝜋
2 𝑓 𝑎 − 𝑥 𝑑𝑥 = 0
𝜋
2
𝑐𝑜𝑠𝑥
3
2 𝑑𝑥
𝑐𝑜𝑠𝑥
3
2+ 𝑠𝑖𝑛𝑥
3
2
------ (3)
Now 2𝐼 = 𝐼 + 𝐼 =
= 0
𝜋
2
𝑠𝑖𝑛𝑥
3
2 𝑑𝑥
𝑠𝑖𝑛𝑥
3
2+ 𝑐𝑜𝑠𝑥
3
2
𝑑𝑥 + 0
𝜋
2
𝑐𝑜𝑠𝑥
3
2 𝑑𝑥
𝑐𝑜𝑠𝑥
3
2+ 𝑠𝑖𝑛𝑥
3
2
, ( By adding (2) & (3))
= 0
𝜋
2
𝑠𝑖𝑛𝑥
3
2
𝑠𝑖𝑛𝑥
3
2+ 𝑐𝑜𝑠𝑥
3
2
+
𝑐𝑜𝑠𝑥
3
2
𝑐𝑜𝑠𝑥
3
2+ 𝑠𝑖𝑛𝑥
3
2
𝑑𝑥
= 0
𝜋
2
𝑠𝑖𝑛𝑥
3
2+ 𝑐𝑜𝑠𝑥
3
2
𝑠𝑖𝑛𝑥
3
2+ 𝑐𝑜𝑠𝑥
3
2
𝑑𝑥 = 0
𝜋
2 𝑑𝑥 = ]
𝑥 0
𝜋
2
=
𝜋
2
− 0 =
𝜋
2
⇒ 2𝐼 =
𝜋
2
⟹ 𝐼 =
𝜋
4
⇒ 0
𝜋
2
𝑠𝑖𝑛𝑥
3
2
𝑠𝑖𝑛𝑥
3
2+ 𝑐𝑜𝑠𝑥
3
2
𝑑𝑥 =
𝜋
4
Problem 3: Evaluate 𝟎
𝝅
𝟐
𝒔𝒊𝒏𝒙
𝟏
𝟐
𝒔𝒊𝒏𝒙
𝟏
𝟐+ 𝒄𝒐𝒔𝒙
𝟏
𝟐
𝒅𝒙
Solution:
Hint : Wkt by the property(8) of definite integral 0
𝑎
𝑓 𝑥 𝑑𝑥 = 0
𝑎
𝑓 𝑎 − 𝑥 𝑑𝑥 -----(1)

69. Let 𝑓 𝑥 =
𝑠𝑖𝑛𝑥
1
2
𝑠𝑖𝑛𝑥
1
2+ 𝑐𝑜𝑠𝑥
1
2
& 𝑎 =
𝜋
2
⇒ 𝑓 𝑎 − 𝑥 =
sin
𝜋
2
−𝑥
1
2
sin
𝜋
2
−𝑥
1
2
+ cos
𝜋
2
−𝑥
1
2
⇒ 𝑓 𝑎 − 𝑥 =
𝑐𝑜𝑠𝑥
1
2
𝑐𝑜𝑠𝑥
1
2+ 𝑠𝑖𝑛𝑥
1
2
, ∵ sin
𝜋
2
− 𝑥 = 𝑐𝑜𝑠𝑥 & cos
𝜋
2
− 𝑥 = 𝑠𝑖𝑛𝑥
And let I = 0
𝜋
2 𝑓 𝑥 𝑑𝑥 = 0
𝜋
2
𝑠𝑖𝑛𝑥
1
2
𝑠𝑖𝑛𝑥
1
2+ 𝑐𝑜𝑠𝑥
1
2
𝑑𝑥 -------- (2)
Then Proceed like Problem 2
Problem 4: Evaluate 𝟎
𝝅
𝟐
𝒔𝒊𝒏 𝜽 𝒏
𝒔𝒊𝒏 𝜽 𝒏 + 𝒄𝒐𝒔 𝜽 𝒏 𝒅𝜽
Solution:
Hint : Wkt by the property(8) of definite integral 0
𝑎
𝑓 𝜃 𝑑𝜃 = 0
𝑎
𝑓 𝑎 − 𝜃 𝑑𝜃 -----(1)

70. Let 𝑓 𝜃 =
𝑠𝑖𝑛𝜃 𝑛
𝑠𝑖𝑛𝜃 𝑛 + 𝑐𝑜𝑠𝜃 𝑛 & 𝑎 =
𝜋
2
⇒ 𝑓 𝑎 − 𝜃 = 𝑓(
𝜋
2
− 𝜃) =
sin
𝜋
2
−𝜃
𝑛
sin
𝜋
2
−𝜃
𝑛
+ cos
𝜋
2
−𝜃
𝑛
⇒ 𝑓
𝜋
2
− 𝜃 =
𝑐𝑜𝑠𝜃 𝑛
𝑐𝑜𝑠𝜃 𝑛 + 𝑠𝑖𝑛𝜃 𝑛 , ∵ sin
𝜋
2
− 𝜃 = 𝑐𝑜𝑠𝜃 & cos
𝜋
2
− 𝜃 = 𝑠𝑖𝑛𝜃
And let I = 0
𝜋
2 𝑓 𝜃 𝑑𝜃 = 0
𝜋
2
𝑠𝑖𝑛𝜃 𝑛
𝑠𝑖𝑛𝜃 𝑛 + 𝑐𝑜𝑠𝜃 𝑛 𝑑𝜃 -------- (2)
Then Proceed like Problem 2
Note : In problem 4, n is any number(n= 1/3,1/2,3/2,….1,…2,…3,… )
Problem 5: Evaluate 𝟎
𝝅 𝒙𝒕𝒂𝒏𝒙
𝒔𝒆𝒄𝒙+𝒄𝒐𝒔𝒙
𝒅𝒙
Solution:
Wkt by the property(8) of definite integral 0
𝑎
𝑓 𝑥 𝑑𝑥 = 0
𝑎
𝑓 𝑎 − 𝑥 𝑑𝑥 -----(1)
Let 𝑓(𝑥) =
𝑥𝑡𝑎𝑛𝑥
𝑠𝑒𝑐𝑥+𝑐𝑜𝑠𝑥
and 𝑎 = 𝜋
⇒ 𝑓(𝑎 − 𝑥) =
(𝑎−𝑥)tan(𝑎−𝑥)
sec(𝑎−𝑥)+cos(𝑎−𝑥)

71. ⇒ 𝑓 𝜋 − 𝑥 =
(𝜋−𝑥)tan(𝜋−𝑥)
sec(𝜋−𝑥)+cos(𝜋−𝑥)
=
−(𝜋−𝑥)tan(𝑥)
− sec 𝑥 −cos(𝑥)
=
−(𝜋−𝑥)tan(𝑥)
− (sec 𝑥 +cos(𝑥))
=
(𝜋−𝑥)tan(𝑥)
(sec 𝑥 +cos(𝑥))
Let 𝐼 = 0
𝜋
𝑓 𝑥 𝑑𝑥= 0
𝜋 𝑥𝑡𝑎𝑛𝑥
𝑠𝑒𝑐𝑥+𝑐𝑜𝑠𝑥
𝑑𝑥------- (2)
From (1) & (2)
𝐼 = 0
𝜋
𝑓 𝑎 − 𝑥 𝑑𝑥 = 0
𝜋 (𝜋−𝑥)tan(𝑥)
(sec 𝑥 +cos(𝑥))
𝑑𝑥 ------ (3)
Now 2𝐼 = 𝐼 + 𝐼 = 0
𝜋 𝑥𝑡𝑎𝑛𝑥
𝑠𝑒𝑐𝑥+𝑐𝑜𝑠𝑥
𝑑𝑥 + 0
𝜋 (𝜋−𝑥)tan(𝑥)
(sec 𝑥 +cos(𝑥))
𝑑𝑥 , (by adding (2)&(3))
= 0
𝜋 𝑥𝑡𝑎𝑛𝑥+ 𝜋−𝑥 𝑡𝑎𝑛𝑥
𝑠𝑒𝑐𝑥+𝑐𝑜𝑠𝑥
𝑑𝑥
= 0
𝜋 𝑥𝑡𝑎𝑛𝑥+𝜋𝑡𝑎𝑛𝑥−𝑥𝑡𝑎𝑛𝑥
𝑠𝑒𝑐𝑥+𝑐𝑜𝑠𝑥
𝑑𝑥
= 0
𝜋 𝜋𝑡𝑎𝑛𝑥
𝑠𝑒𝑐𝑥+𝑐𝑜𝑠𝑥
𝑑𝑥
2𝐼 = 𝜋 0
𝜋 𝑡𝑎𝑛𝑥
𝑠𝑒𝑐𝑥+𝑐𝑜𝑠𝑥
𝑑𝑥 -------- (4)

72. Consider
𝑡𝑎𝑛𝑥
𝑠𝑒𝑐𝑥+𝑐𝑜𝑠𝑥
𝑑𝑥
𝑡𝑎𝑛𝑥
𝑠𝑒𝑐𝑥+𝑐𝑜𝑠𝑥
𝑑𝑥 =
𝑠𝑖𝑛𝑥
𝑐𝑜𝑠𝑥
1
𝑐𝑜𝑠𝑥
+𝑐𝑜𝑠𝑥
𝑑𝑥
=
𝑠𝑖𝑛𝑥
𝑐𝑜𝑠𝑥
1+cos2 𝑥
𝑐𝑜𝑠𝑥
𝑑𝑥
=
𝑠𝑖𝑛𝑥
1+cos2 𝑥
𝑑𝑥
Put 𝑡 = cos 𝑥 ⇒ 𝑑𝑡 = −𝑠𝑖𝑛𝑥 𝑑𝑥 ⇒ 𝑠𝑖𝑛𝑥 𝑑𝑥 = −𝑑𝑡
𝑡𝑎𝑛𝑥
𝑠𝑒𝑐𝑥+𝑐𝑜𝑠𝑥
𝑑𝑥 =
−𝑑𝑡
1+𝑡2
= −
𝑑𝑡
1+𝑡2
= − tan−1
𝑡
∴
𝑡𝑎𝑛𝑥
𝑠𝑒𝑐𝑥+𝑐𝑜𝑠𝑥
𝑑𝑥 = − tan−1
(𝑐𝑜𝑠𝑥) -------- (5)

73. From (4) & (5)
2𝐼 = 𝜋 0
𝜋 𝑡𝑎𝑛𝑥
𝑠𝑒𝑐𝑥+𝑐𝑜𝑠𝑥
𝑑𝑥 = 𝜋 ]
(− tan−1
𝑐𝑜𝑠𝑥 0
𝜋
)
= −𝜋(tan−1
𝑐𝑜𝑠𝜋 − tan−1
(𝑐𝑜𝑠0))
= −𝜋 (tan−1
−1 − tan−1
1 ) , (∵ 𝑐𝑜𝑠𝜋 = −1, 𝑐𝑜𝑠0 = 1)
= −𝜋 −
𝜋
4
−
𝜋
4
, (∵ tan−1
−1 = −
𝜋
4
, tan−1
1 =
𝜋
4
)
= −𝜋 −
𝜋
2
∴ 2𝐼 =
𝜋2
2
⇒ 𝐼 =
𝜋2
4
∴ 0
𝜋 𝑥𝑡𝑎𝑛𝑥
𝑠𝑒𝑐𝑥+𝑐𝑜𝑠𝑥
𝑑𝑥 =
𝜋2
4
Problem 6: Evaluate 𝟎
𝝅
𝟐 𝐥𝐨𝐠 𝒕𝒂𝒏𝒙 𝒅𝒙
Solution:
Wkt by the property(8) of definite integral 0
𝑎
𝑓 𝑥 𝑑𝑥 = 0
𝑎
𝑓 𝑎 − 𝑥 𝑑𝑥 -----(1)
Let 𝑓 𝑥 = log(𝑡𝑎𝑛𝑥) and 𝑎 =
𝜋
2
⇒ 𝑓 𝑎 − 𝑥 = 𝑓
𝜋
2
− 𝑥 = log tan
𝜋
2
− 𝑥

74. ⇒ 𝑓
𝜋
2
− 𝑥 = log tan
𝜋
2
− 𝑥 = log 𝑐𝑜𝑡𝑥
= log
1
𝑡𝑎𝑛𝑥
, ∵ 𝑐𝑜𝑡𝑥 =
1
𝑡𝑎𝑛𝑥
= log 1 − log(𝑡𝑎𝑛𝑥) , ∵ log
𝑎
𝑏
= 𝑙𝑜𝑔𝑎 − 𝑙𝑜𝑔𝑏
= 0 − log 𝑡𝑎𝑛𝑥 = −log(𝑡𝑎𝑛𝑥) , ∵ log 1 = 0
∴ 𝑓 𝑎 − 𝑥 = 𝑓
𝜋
2
− 𝑥 = −log(𝑡𝑎𝑛𝑥) ------ (2)
Let 𝐼 = 0
𝜋
2 𝑓 𝑥 𝑑𝑥 = 0
𝜋
2 log 𝑡𝑎𝑛𝑥 𝑑𝑥 ------(3)
From (1) , (2) & (3)
𝐼 = 0
𝜋
2 𝑓
𝜋
2
− 𝑥 𝑑𝑥 = 0
𝜋
2 − log 𝑡𝑎𝑛𝑥 𝑑𝑥 = − 0
𝜋
2 log 𝑡𝑎𝑛𝑥 𝑑𝑥 -----(4)
Now 2𝐼 = 𝐼 + 𝐼 = 0
𝜋
2 log 𝑡𝑎𝑛𝑥 𝑑𝑥 − 0
𝜋
2 log 𝑡𝑎𝑛𝑥 𝑑𝑥, (by (3) & (4))
⇒ 2𝐼 = 0 ⇒ 𝐼 = 0
∴ 0
𝜋
2 log 𝑡𝑎𝑛𝑥 𝑑𝑥 = 0

75. Problem 7: If 𝟎
𝟏𝟎
𝒇 𝒙 𝒅𝒙 = 𝟏𝟕, 𝟎
𝟖
𝒇 𝒙 𝒅𝒙 = 𝟏𝟐, then find 𝟖
𝟏𝟎
𝒇 𝒙 𝒅𝒙
Solution:
Given 0
10
𝑓 𝑥 𝑑𝑥 = 17, 0
8
𝑓 𝑥 𝑑𝑥 = 12 --------(1)
8
10
𝑓 𝑥 𝑑𝑥 = 8
0
𝑓 𝑥 𝑑𝑥 + 0
10
𝑓 𝑥 𝑑𝑥
= − 0
8
𝑓 𝑥 𝑑𝑥 + 0
10
𝑓 𝑥 𝑑𝑥 ------- (2)
(∵ by the properties, 𝑎
𝑏
𝑓 𝑥 𝑑𝑥 = 𝑎
𝑐
𝑓 𝑥 𝑑𝑥 + 𝑐
𝑏
𝑓 𝑥 𝑑𝑥 & 𝑎
𝑏
𝑓 𝑥 𝑑𝑥 = − 𝑏
𝑎
𝑓 𝑥 𝑑𝑥 )
∴
8
10
𝑓 𝑥 𝑑𝑥 = 12 − 17 = −5 , (by using (1) in (2))
Problem 8: Find the value of 𝟐
𝟗
𝒇 𝒙 𝒅𝒙, given that 𝟓
𝟐
𝒇 𝒙 = 𝟑 , 𝟓
𝟗
𝒇 𝒙 𝒅𝒙 = 𝟖
Solution:
Given 5
2
𝑓 𝑥 = 3 , 5
9
𝑓 𝑥 𝑑𝑥 = 8 -------- (1)
2
9
𝑓 𝑥 𝑑𝑥 = 2
5
𝑓 𝑥 𝑑𝑥 + 5
9
𝑓 𝑥 𝑑𝑥 = − 5
2
𝑓 𝑥 𝑑𝑥 + 5
9
𝑓 𝑥 𝑑𝑥 ------ (2)
(∵ by the properties, 𝑎
𝑏
𝑓 𝑥 𝑑𝑥 = 𝑎
𝑐
𝑓 𝑥 𝑑𝑥 + 𝑐
𝑏
𝑓 𝑥 𝑑𝑥 & 𝑎
𝑏
𝑓 𝑥 𝑑𝑥 = − 𝑏
𝑎
𝑓 𝑥 𝑑𝑥 )
∴ 2
9
𝑓 𝑥 𝑑𝑥 = −3 + 8 = 5, (by using (1) in (2))

76. Problem 9: If f is continuous and 𝟎
𝟒
𝒇 𝒙 𝒅𝒙 = 𝟏𝟎, find 𝟎
𝟐
𝒇 𝟐𝒙 𝒅𝒙
Solution:
Given 0
4
𝑓 𝑥 𝑑𝑥 = 10
To find 0
2
𝑓 2𝑥 𝑑𝑥
Let 𝑡 = 2𝑥 ⇒ 𝑑𝑡 = 2𝑑𝑥 ⇒ 𝑑𝑥 =
𝑑𝑡
2
When 𝑥 = 0, 𝑡 = 2 0 = 0
When 𝑥 = 2, 𝑡 = 2 2 = 4
Hence 0
2
𝑓 2𝑥 𝑑𝑥 = 0
4
𝑓 𝑡
𝑑𝑡
2
=
1
2 0
4
𝑓 𝑡 𝑑𝑡 =
1
2
10 = 5 , (∵ 0
4
𝑓 𝑥 𝑑𝑥 = 0
4
𝑓 𝑡 𝑑𝑡 = 10)

77. Integration by parts
If u and v are any two integrable functions, then
𝑢 𝑑𝑣 = 𝑢𝑣 − 𝑣 𝑑𝑢
Note:
To choose u →
I LATE
I-Inverse Trigonometric
L-Logarithm
A-Algebraic
T-Trigonometric
E-Exponential
Bernoulli’s formula
𝑢𝑑𝑣 = 𝑢𝑣 − 𝑢′𝑣1 + 𝑢′′𝑣2 + ⋯
Where 𝑢′
=
𝑑𝑢
𝑑𝑥
, 𝑢′′
=
𝑑2𝑢
𝑑𝑥2 , … .
𝑣1 = 𝑣 𝑑𝑥 , 𝑣2 = 𝑣1𝑑𝑥 , …

78. Problem 1: Find 𝒙 𝒆𝒙
𝒅𝒙
Solution:
Given function is 𝑥 𝑒𝑥
𝑥 − A−Algebraic function
𝑒𝑥
− E−Exponential function
Rule: To choose 𝒖 → I LATE
Here 𝑢 = 𝑥 & 𝑑𝑣 = 𝑒𝑥
𝑑𝑥
⟹ 𝑑𝑢 = 𝑑𝑥 & 𝑣 = 𝑑𝑣 = 𝑒𝑥
𝑑𝑥 = 𝑒𝑥
Wkt 𝑢 𝑑𝑣 = 𝑢𝑣 − 𝑣 𝑑𝑢
𝑥 𝑒𝑥
𝑑𝑥 = 𝑥𝑒𝑥
− 𝑒𝑥
𝑑𝑥
= 𝑥𝑒𝑥
− 𝑒𝑥
= 𝑒𝑥
(𝑥 − 1)
Problem 2: Find 𝐭𝐚𝐧−𝟏
𝒙 𝒅𝒙
Solution:
Given function is tan−1
𝑥
tan−1
𝑥 -I -Inverse function
1- A−Algebraic function
Rule: To choose 𝒖 → I LATE
Here 𝑢 = tan−1
𝑥 & 𝑑𝑣 = 1. 𝑑𝑥 = 𝑑𝑥
𝑑𝑢 =
1
1+𝑥2 𝑑𝑥 & 𝑣 = 𝑑𝑣 = 𝑑𝑥 = 𝑥

79. Wkt 𝑢 𝑑𝑣 = 𝑢𝑣 − 𝑣 𝑑𝑢 ( Note: 𝑢 𝑑𝑣 = (tan−1 𝑥) 𝑑 (𝑥) )
tan−1
𝑥 𝑑𝑥 = 𝑥 tan−1
𝑥 −
𝑥
1+𝑥2 𝑑𝑥 ------ (1)
Consider
𝑥
1+𝑥2 𝑑𝑥
Put 𝑡 = 1 + 𝑥2
⇒ 𝑑𝑡 = 2𝑥𝑑𝑥 ⇒ 𝑥𝑑𝑥 =
𝑑𝑡
2
𝑥
1+𝑥2 𝑑𝑥 =
𝑑𝑡
2
𝑡
=
𝑑𝑡
2𝑡
=
1
2
𝑑𝑡
𝑡
=
1
2
𝑙𝑜𝑔𝑡 =
1
2
log(1 + 𝑥2
) , (∵
𝑑𝑥
𝑥
= 𝑙𝑜𝑔𝑥)--------(2)
From (1) & (2) ,
tan−1
𝑥 𝑑𝑥 = 𝑥 tan−1
𝑥 −
1
2
log(1 + 𝑥2
)
Note : 0
1
tan−1
𝑥 𝑑𝑥 = 𝑥 tan−1
𝑥 −
1
2
log 1 + 𝑥2
0
1
= 1. tan−1
1 −
1
2
log 1 + 12
− 0. tan−1
0 −
1
2
log 1 + 0
=
𝜋
4
−
1
2
𝑙𝑜𝑔2 − (0 −
1
2
𝑙𝑜𝑔1)
=
𝜋
4
−
1
2
𝑙𝑜𝑔2 − 0 , ∵ tan−1
1 =
𝜋
4
, log 1 = 0
=
𝜋
4
−
1
2
𝑙𝑜𝑔2

80. Problem 3: Evaluate 𝒍𝒐𝒈𝒙 𝟐
𝒅𝒙
Solution:
Given function is 𝑙𝑜𝑔𝑥 2
𝑙𝑜𝑔𝑥 2
- L-Logarithmic function
1- A−Algebraic function
Rule: To choose 𝒖 → I LATE
Here 𝑢 = 𝑙𝑜𝑔𝑥 2
& 𝑑𝑣 = 1. 𝑑𝑥
𝑑𝑢 = 2 𝑙𝑜𝑔𝑥.
𝑑𝑥
𝑥
& 𝑣 = 𝑑𝑣 = 𝑑𝑥 = 𝑥
Wkt 𝑢 𝑑𝑣 = 𝑢𝑣 − 𝑣 𝑑𝑢 ( Note : 𝑢 𝑑𝑣 = 𝑙𝑜𝑔𝑥 2
𝑑𝑥 )
𝑙𝑜𝑔𝑥 2
𝑑𝑥 = 𝑥 𝑙𝑜𝑔𝑥 2
− 𝑥. 2 𝑙𝑜𝑔𝑥.
𝑑𝑥
𝑥
𝑙𝑜𝑔𝑥 2
𝑑𝑥 = 𝑥 𝑙𝑜𝑔𝑥 2
− 2 𝑙𝑜𝑔𝑥 𝑑𝑥 ------- (1)
Consider 𝑙𝑜𝑔𝑥 𝑑𝑥
𝑙𝑜𝑔𝑥 - L-Logarithmic function
1- A−Algebraic function
Rule: To choose 𝒖 → I LATE
Here 𝑢 = 𝑙𝑜𝑔𝑥 & 𝑑𝑣 = 1. 𝑑𝑥
𝑑𝑢 =
𝑑𝑥
𝑥
& 𝑣 = 𝑑𝑣 = 𝑑𝑥 = 𝑥
Wkt 𝑢 𝑑𝑣 = 𝑢𝑣 − 𝑣 𝑑𝑢

81. 𝑙𝑜𝑔𝑥 𝑑𝑥 = 𝑥𝑙𝑜𝑔𝑥 − 𝑥.
𝑑𝑥
𝑥
= 𝑥𝑙𝑜𝑔𝑥 − 𝑑𝑥
𝑙𝑜𝑔𝑥 𝑑𝑥 = 𝑥𝑙𝑜𝑔𝑥 − 𝑥 ------- (2)
From (1) & (2),
𝑙𝑜𝑔𝑥 2
𝑑𝑥 = 𝑥 𝑙𝑜𝑔𝑥 2
− 2 𝑙𝑜𝑔𝑥 𝑑𝑥
= 𝑥 𝑙𝑜𝑔𝑥 2
− 2(𝑥𝑙𝑜𝑔𝑥 − 𝑥)
= 𝑥 𝑙𝑜𝑔𝑥 2 − 2𝑥𝑙𝑜𝑔𝑥 + 2𝑥
Problem 4: Evaluate 𝒙 𝒄𝒐𝒔𝒙 𝒅𝒙
Solution:
Here 𝑢 = 𝑥 & 𝑑𝑣 = 𝑐𝑜𝑠𝑥 𝑑𝑥
𝑑𝑢 = 𝑑𝑥 & 𝑣 = 𝑑𝑣 = 𝑐𝑜𝑠𝑥 𝑑𝑥 = 𝑠𝑖𝑛𝑥
Wkt 𝑢 𝑑𝑣 = 𝑢𝑣 − 𝑣 𝑑𝑢
𝑥 𝑐𝑜𝑠𝑥 𝑑𝑥 = 𝑥 𝑠𝑖𝑛𝑥 − 𝑠𝑖𝑛𝑥 𝑑𝑥
= 𝑥𝑠𝑖𝑛𝑥 − −𝑐𝑜𝑠𝑥 = 𝑥𝑠𝑖𝑛𝑥 + 𝑐𝑜𝑠𝑥

82. Problem 5: Evaluate
𝒍𝒐𝒈𝒙
𝒙𝟐 𝒅𝒙
Solution:
Here 𝑢 = 𝑙𝑜𝑔𝑥 & 𝑑𝑣 =
𝑑𝑥
𝑥2
𝑑𝑢 =
1
𝑥
𝑑𝑥 & 𝑣 = 𝑑𝑣 =
𝑑𝑥
𝑥2 = −
1
𝑥
Wkt 𝑢 𝑑𝑣 = 𝑢𝑣 − 𝑣 𝑑𝑢
𝑙𝑜𝑔𝑥
𝑥2 𝑑𝑥 = −
𝑙𝑜𝑔𝑥
𝑥
− −
1
𝑥
1
𝑥
𝑑𝑥
= −
𝑙𝑜𝑔𝑥
𝑥
+
𝑑𝑥
𝑥2
= −
𝑙𝑜𝑔𝑥
𝑥
−
1
𝑥
Problem 6: Evaluate
𝒍𝒐𝒈𝒙 𝟐
𝒙𝟐 𝒅𝒙
Solution:
Here 𝑢 = 𝑙𝑜𝑔𝑥 2 & 𝑑𝑣 =
𝑑𝑥
𝑥2
𝑑𝑢 =
2𝑙𝑜𝑔𝑥
𝑥
𝑑𝑥 & 𝑣 = 𝑑𝑣 =
𝑑𝑥
𝑥2 = −
1
𝑥
Wkt 𝑢 𝑑𝑣 = 𝑢𝑣 − 𝑣 𝑑𝑢

83. 𝑙𝑜𝑔𝑥 2
𝑥2 𝑑𝑥 = −
𝑙𝑜𝑔𝑥 2
𝑥
− −
1
𝑥
2 𝑙𝑜𝑔𝑥
𝑥
𝑑𝑥
= −
𝑙𝑜𝑔𝑥 2
𝑥
+ 2
𝑙𝑜𝑔𝑥
𝑥2 𝑑𝑥 ------- (1)
Consider
𝑙𝑜𝑔𝑥
𝑥2 𝑑𝑥
Here 𝑢 = 𝑙𝑜𝑔𝑥 & 𝑑𝑣 =
𝑑𝑥
𝑥2
𝑑𝑢 =
1
𝑥
𝑑𝑥 & 𝑣 = 𝑑𝑣 =
𝑑𝑥
𝑥2 = −
1
𝑥
Wkt 𝑢 𝑑𝑣 = 𝑢𝑣 − 𝑣 𝑑𝑢
𝑙𝑜𝑔𝑥
𝑥2 𝑑𝑥 = −
𝑙𝑜𝑔𝑥
𝑥
− −
1
𝑥
1
𝑥
𝑑𝑥
= −
𝑙𝑜𝑔𝑥
𝑥
+
𝑑𝑥
𝑥2
𝑙𝑜𝑔𝑥
𝑥2 𝑑𝑥 = −
𝑙𝑜𝑔𝑥
𝑥
−
1
𝑥
------- (2)
From (1) & (2) ,
𝑙𝑜𝑔𝑥 2
𝑥2 𝑑𝑥 = −
𝑙𝑜𝑔𝑥 2
𝑥
+ 2
𝑙𝑜𝑔𝑥
𝑥2 𝑑𝑥
= −
𝑙𝑜𝑔𝑥 2
𝑥
+ 2(−
𝑙𝑜𝑔𝑥
𝑥
−
1
𝑥
)
= −
𝑙𝑜𝑔𝑥 2
𝑥
−
2𝑙𝑜𝑔𝑥
𝑥
−
2
𝑥

84. Problem 7: Evaluate 𝒆𝒂𝒙𝒄𝒐𝒔𝒃𝒙 𝒅𝒙
Solution:
Let 𝐼 = 𝑒𝑎𝑥
𝑐𝑜𝑠𝑏𝑥 𝑑𝑥 ---------- (1)
Here 𝑢 = 𝑐𝑜𝑠𝑏𝑥 & 𝑑𝑣 = 𝑒𝑎𝑥
𝑑𝑥
𝑑𝑢 = −𝑏 𝑠𝑖𝑛𝑏𝑥 𝑑𝑥 & 𝑣 = 𝑑𝑣 = 𝑒𝑎𝑥 𝑑𝑥 =
𝑒𝑎𝑥
𝑎
Wkt 𝑢 𝑑𝑣 = 𝑢𝑣 − 𝑣 𝑑𝑢
𝐼 = 𝑒𝑎𝑥
𝑐𝑜𝑠𝑏𝑥 𝑑𝑥 =
𝑒𝑎𝑥
𝑎
𝑐𝑜𝑠𝑏𝑥 −
𝑒𝑎𝑥
𝑎
− 𝑏𝑠𝑖𝑛𝑏𝑥 𝑑𝑥
𝐼 =
𝑒𝑎𝑥
𝑎
𝑐𝑜𝑠𝑏𝑥 +
𝑏
𝑎
𝑒𝑎𝑥
𝑠𝑖𝑛𝑏𝑥 𝑑𝑥 ------- (2)
Consider 𝑒𝑎𝑥𝑠𝑖𝑛𝑏𝑥 𝑑𝑥
Here 𝑢 = 𝑠𝑖𝑛𝑏𝑥 & 𝑑𝑣 = 𝑒𝑎𝑥
𝑑𝑥
𝑑𝑢 = 𝑏 𝑐𝑜𝑠𝑏𝑥 𝑑𝑥 & 𝑣 = 𝑑𝑣 = 𝑒𝑎𝑥
𝑑𝑥 =
𝑒𝑎𝑥
𝑎
Wkt 𝑢 𝑑𝑣 = 𝑢𝑣 − 𝑣 𝑑𝑢
𝑒𝑎𝑥𝑠𝑖𝑛𝑏𝑥 𝑑𝑥 =
𝑒𝑎𝑥
𝑎
𝑠𝑖𝑛𝑏𝑥 −
𝑒𝑎𝑥
𝑎
𝑏𝑐𝑜𝑠𝑏𝑥 𝑑𝑥

85. 𝑒𝑎𝑥
𝑠𝑖𝑛𝑏𝑥 𝑑𝑥 =
𝑒𝑎𝑥
𝑎
𝑠𝑖𝑛𝑏𝑥 −
𝑏
𝑎
𝑒𝑎𝑥
𝐶𝑜𝑠𝑏𝑥𝑑𝑥
𝑒𝑎𝑥
𝑠𝑖𝑛𝑏𝑥 𝑑𝑥 =
𝑒𝑎𝑥
𝑎
𝑠𝑖𝑛𝑏𝑥 −
𝑏
𝑎
𝐼 , ∵ 𝑏𝑦 𝑢𝑠𝑖𝑛𝑔 1 -------- (3)
From (2) & (3)
𝐼 =
𝑒𝑎𝑥
𝑎
𝑐𝑜𝑠𝑏𝑥 +
𝑏
𝑎
𝑒𝑎𝑥
𝑎
𝑠𝑖𝑛𝑏𝑥 −
𝑏𝐼
𝑎
𝐼 =
𝑒𝑎𝑥
𝑎
𝑐𝑜𝑠𝑏𝑥 +
𝑒𝑎𝑥
𝑎2 𝑠𝑖𝑛𝑏𝑥 −
𝑏2𝐼
𝑎2
𝐼 +
𝑏2𝐼
𝑎2 =
𝑒𝑎𝑥
𝑎
𝑐𝑜𝑠𝑏𝑥 +
𝑏𝑒𝑎𝑥
𝑎2 𝑠𝑖𝑛𝑏𝑥
𝐼 1 +
𝑏2
𝑎2 =
𝑒𝑎𝑥
𝑎2 𝑎𝑐𝑜𝑠𝑏𝑥 + 𝑏𝑠𝑖𝑛𝑏𝑥
𝐼
𝑎2+𝑏2
𝑎2 =
𝑒𝑎𝑥
𝑎2 (𝑎𝑐𝑜𝑠𝑏𝑥 + 𝑏𝑠𝑖𝑛𝑏𝑥)
𝐼(𝑎2
+ 𝑏2
) = 𝑒𝑎𝑥
(𝑎𝑐𝑜𝑠𝑏𝑥 + 𝑏𝑠𝑖𝑛𝑏𝑥)
𝐼 =
𝑒𝑎𝑥
𝑎2+𝑏2 (𝑎𝑐𝑜𝑠𝑏𝑥 + 𝑏𝑠𝑖𝑛𝑏𝑥)
∴ 𝑒𝑎𝑥𝑐𝑜𝑠𝑏𝑥 𝑑𝑥 =
𝑒𝑎𝑥
𝑎2+𝑏2 (𝑎𝑐𝑜𝑠𝑏𝑥 + 𝑏𝑠𝑖𝑛𝑏𝑥)

86. Problem 8: Evaluate 𝒆𝒂𝒙
𝒔𝒊𝒏𝒃𝒙 𝒅𝒙
Solution:
Proceed as per the problem 7, Here 𝑢 = 𝑠𝑖𝑛𝑏𝑥 & 𝑑𝑣 = 𝑒𝑎𝑥
𝑑𝑥
Ans:
𝑒𝑎𝑥
𝑎2+𝑏2 (𝑎𝑠𝑖𝑛𝑏𝑥 − 𝑏𝑐𝑜𝑠𝑏𝑥)
Problem 9: Evaluate 𝒆−𝒂𝒙
𝐜𝐨𝐬 𝒃𝒙 𝒅𝒙
Solution:
Proceed as per the problem 7, Here 𝑢 = 𝑐𝑜𝑠𝑏𝑥 & 𝑑𝑣 = 𝑒−𝑎𝑥
𝑑𝑥
Ans:
𝑒−𝑎𝑥
𝑎2+𝑏2 (−𝑎𝑐𝑜𝑠𝑏𝑥 + 𝑏𝑠𝑖𝑛𝑏𝑥)
Problem 10: Evaluate 𝒆−𝒂𝒙
𝐬𝐢𝐧 𝒃𝒙 𝒅𝒙
Solution:
Proceed as per the problem 7, Here 𝑢 = 𝑠𝑖𝑛𝑏𝑥 & 𝑑𝑣 = 𝑒−𝑎𝑥𝑑𝑥
Ans:
𝑒−𝑎𝑥
𝑎2+𝑏2 (−𝑎𝑠𝑖𝑛𝑏𝑥 − 𝑏𝑐𝑜𝑠𝑏𝑥)

87. Problem 11: Evaluate 𝒙𝟒𝒆𝒙𝒅𝒙
Solution:
Here 𝑢 = 𝑥4
& 𝑑𝑣 = 𝑒𝑥
𝑑𝑥
Wkt Bernoulli’s formula 𝑢𝑑𝑣 = 𝑢𝑣 − 𝑢′
𝑣1 + 𝑢′′
𝑣2 + ⋯ ------ (1)
𝑢 = 𝑥3
𝑑𝑣 = 𝑒𝑥
𝑑𝑥
𝑢′ = 4𝑥3
𝑣 = 𝑑𝑣 = 𝑒𝑥𝑑𝑥 = 𝑒𝑥
𝑢′′ = 12𝑥2
𝑣1 = 𝑣 𝑑𝑥 = 𝑒𝑥𝑑𝑥 = 𝑒𝑥
𝑢′′′
= 24𝑥
𝑣2 = 𝑣1𝑑𝑥 = 𝑒𝑥𝑑𝑥 = 𝑒𝑥
𝑢𝑖𝑣 = 24
𝑣3 = 𝑣2𝑑𝑥 = 𝑒𝑥𝑑𝑥 = 𝑒𝑥
𝑣4 = 𝑣3𝑑𝑥 = 𝑒𝑥𝑑𝑥 = 𝑒𝑥

88. From (1),
𝑥4𝑒𝑥𝑑𝑥 = 𝑥4𝑒𝑥 − 4𝑥3𝑒𝑥 + 12𝑥2𝑒𝑥 + 24𝑥𝑒𝑥 + 24𝑒𝑥
Problem 12 : Evaluate 𝒙𝟑
𝒄𝒐𝒔𝟐𝒙 𝒅𝒙
Solution:
Here 𝑢 = 𝑥3
& 𝑑𝑣 = 𝑐𝑜𝑠2𝑥 𝑑𝑥
Wkt Bernoulli’s formula 𝑢𝑑𝑣 = 𝑢𝑣 − 𝑢′𝑣1 + 𝑢′′𝑣2 + ⋯ ------ (1)
𝑢 = 𝑥3
𝑑𝑣 = 𝑐𝑜𝑠2𝑥𝑑𝑥
𝑢′ = 3𝑥2
𝑣 = 𝑑𝑣 = 𝑐𝑜𝑠2𝑥 𝑑𝑥 =
𝑠𝑖𝑛2𝑥
2
𝑢′′
= 6𝑥 𝑣1 = 𝑣 𝑑𝑥 =
𝑠𝑖𝑛2𝑥
2
𝑑𝑥 =
1
2
𝑠𝑖𝑛2𝑥 𝑑𝑥
=
1
2
−𝑐𝑜𝑠2𝑥
2
= −
𝑐𝑜𝑠2𝑥
4
𝑢′′′ = 6 𝑣2 = −
𝑐𝑜𝑠2𝑥
4
𝑑𝑥 = −
1
4
𝑐𝑜𝑠2𝑥 𝑑𝑥
= −
1
4
𝑠𝑖𝑛2𝑥
2
= −
𝑠𝑖𝑛2𝑥
8
𝑣3 =
−𝑠𝑖𝑛2𝑥
8
𝑑𝑥 = −
1
8
𝑠𝑖𝑛2𝑥 𝑑𝑥
= −
1
8
−𝑐𝑜𝑠2𝑥
2
=
𝐶𝑜𝑠2𝑥
16

89. From (1),
𝑥3
𝐶𝑜𝑠2𝑥𝑑𝑥 = 𝑥3 𝑠𝑖𝑛2𝑥
2
− 3𝑥2
−
𝐶𝑜𝑠2𝑥
4
+ 6𝑥 −
𝑆𝑖𝑛2𝑥
8
− 6
𝐶𝑜𝑠2𝑥
16
=
1
2
𝑥3𝑆𝑖𝑛2𝑥 +
3𝑥2𝐶𝑜𝑠2𝑥
2
−
6𝑥𝑆𝑖𝑛2𝑥
4
−
6𝐶𝑜𝑠2𝑥
8
=
1
2
𝑥3𝑆𝑖𝑛2𝑥 +
3𝑥2𝐶𝑜𝑠2𝑥
2
−
3𝑥𝑆𝑖𝑛2𝑥
2
−
3𝐶𝑜𝑠2𝑥
4

90. Reduction formula
1. 0
𝜋
2 𝑆𝑖𝑛𝑛
𝑥 𝑑𝑥 =
𝑛−1
𝑛
𝑛−3
𝑛−2
…
1
2
𝜋
2
, 𝑖𝑓 𝑛 𝑠 𝑒𝑣𝑒n
𝑛−1
𝑛
𝑛−3
𝑛−2
…
2
3
, 𝑖𝑓 𝑛 𝑖𝑠 𝑜𝑑𝑑
2. 0
𝜋
2 cos𝑛 𝑥 𝑑𝑥 =
𝑛−1
𝑛
𝑛−3
𝑛−2
…
1
2
𝜋
2
, 𝑖𝑓 𝑛 𝑠 𝑒𝑣𝑒𝑛
𝑛−1
𝑛
𝑛−3
𝑛−2
…
2
3
, 𝑖𝑓 𝑛 𝑖𝑠 𝑜𝑑𝑑
3. 0
𝜋
2 sin𝑚
𝑥 cos𝑛
𝑥 𝑑𝑥 =
𝑛−1
𝑚+𝑛
𝑛−3
𝑚+𝑛−2
…
2
𝑚+3
1
𝑚+1
, 𝑖𝑓 𝑛 𝑖𝑠 𝑜𝑑𝑑
𝑛−1
𝑚+𝑛
𝑛−3
𝑚+𝑛−2
…
1
𝑚+2
𝑚−1
𝑚
𝑚−3
𝑚−2
…
1
2
𝜋
2
, 𝑖𝑓 𝑛 𝑖𝑠 𝑒𝑣𝑒𝑛
Problem 1 : Establish the reduction formula for 𝐬𝐢𝐧𝒏
𝒙 𝒅𝒙
Hence find 𝟎
𝝅
𝟐 𝐬𝐢𝐧𝒏
𝒙 𝒅𝒙
Solution:
Let 𝐼𝑛 = sin𝑛
𝑥 𝑑𝑥
= sin𝑛−1
𝑥 𝑠𝑖𝑛𝑥 𝑑𝑥

91. = sin𝑛−1
𝑥 𝑠𝑖𝑛𝑥 𝑑𝑥
Here take 𝑢 = sin𝑛−1 𝑥 & 𝑑𝑣 = 𝑠𝑖𝑛𝑥𝑑𝑥
𝑑𝑢 = 𝑛 − 1 sin𝑛−2
𝑥 𝑐𝑜𝑠𝑥 𝑑𝑥 & 𝑣 = 𝑑𝑣 = 𝑠𝑖𝑛𝑥𝑑𝑥 = −𝑐𝑜𝑠𝑥
Wkt 𝑢𝑑𝑣 = 𝑢𝑣 − 𝑣 𝑑𝑢
∴ 𝐼𝑛= sin𝑛−1
𝑥(−𝑐𝑜𝑠𝑥) − −𝑐𝑜𝑠𝑥 𝑛 − 1 sin𝑛−2
𝑥 𝑐𝑜𝑠𝑥 𝑑𝑥
= −𝑐𝑜𝑠𝑥 𝑠𝑖𝑛𝑛−1
𝑥 + (𝑛 − 1) sin𝑛−2
𝑥 cos2
𝑥 𝑑𝑥
= −𝑐𝑜𝑠𝑥 sin𝑛−1
𝑥 + (𝑛 − 1) sin𝑛−2
𝑥(1 − sin2
𝑥) 𝑑𝑥, (∵ cos2
𝑥 = 1 − sin2
𝑥)
= −𝑐𝑜𝑠𝑥 sin𝑛−1 𝑥 + (𝑛 − 1) sin𝑛−2 𝑥 𝑑𝑥 − (𝑛 − 1) sin𝑛−2 𝑥 sin2 𝑥 𝑑𝑥
= −𝑐𝑜𝑠𝑥 sin𝑛−1
𝑥 + (𝑛 − 1) sin𝑛−2
𝑥 𝑑𝑥 − (𝑛 − 1) sin𝑛−2+2
𝑥 𝑑𝑥
𝐼𝑛 = −𝑐𝑜𝑠𝑥 sin𝑛−1 𝑥 + (𝑛 − 1) sin𝑛−2 𝑥 𝑑𝑥 − (𝑛 − 1) sin𝑛 𝑥 𝑑𝑥
⇒ 𝐼𝑛 = −𝑐𝑜𝑠𝑥 sin𝑛−1
𝑥 + (𝑛 − 1)𝐼𝑛−2 − (𝑛 − 1)𝐼𝑛,
(∵ 𝐼𝑛 = sin𝑛
𝑥 𝑑𝑥 ⇒ 𝐼𝑛−2 = sin𝑛−2
𝑥 𝑑𝑥)
⇒ 𝐼𝑛 + 𝑛 − 1 𝐼𝑛 = −𝑐𝑜𝑠𝑥 sin𝑛−1
𝑥 + 𝑛 − 1 𝐼𝑛−2
⇒ 𝐼𝑛 +𝑛𝐼𝑛 − 𝐼𝑛 = −𝑐𝑜𝑠𝑥 sin𝑛−1
𝑥 + 𝑛 − 1 𝐼𝑛−2
⇒ 𝑛𝐼𝑛 = −𝑐𝑜𝑠𝑥 sin𝑛−1
𝑥 + 𝑛 − 1 𝐼𝑛−2
⇒ 𝐼𝑛= −
𝑐𝑜𝑠𝑥 sin𝑛−1 𝑥
𝑛
+
𝑛−1
𝑛
𝐼𝑛−2

92. Hence sin𝑛
𝑥 𝑑𝑥 = −
𝑐𝑜𝑠𝑥 sin𝑛−1 𝑥
𝑛
+
𝑛−1
𝑛
𝐼𝑛−2,
which is the required reduction formula.
Deduction: 𝟎
𝝅
𝟐 𝒔𝒊𝒏𝒏
𝒙 𝒅𝒙
0
𝜋
2 sin𝑛 𝑥 𝑑𝑥 = −
𝑐𝑜𝑠𝑥 sin𝑛−1 𝑥
𝑛 0
𝜋
2
+
𝑛−1
𝑛 0
𝜋
2 sin𝑛−2 𝑥 𝑑𝑥
= 0 − 0 +
𝑛−1
𝑛 0
𝜋
2 sin𝑛−2
𝑥 𝑑𝑥 , (∵ cos
𝜋
2
= 0, sin 0 = 0)
∴ 0
𝜋
2 sin𝑛
𝑥 𝑑𝑥 =
𝑛−1
𝑛 0
𝜋
2 sin𝑛−2
𝑥 𝑑𝑥 ------ (1)
Put 𝑛 = 𝑛 − 2 in (1)
0
𝜋
2 sin𝑛−2
𝑥 𝑑𝑥 =
(𝑛−2)−1
𝑛−2 0
𝜋
2 sin(𝑛−2)−2
𝑥 𝑑𝑥
∴ 0
𝜋
2 sin𝑛−2
𝑥 𝑑𝑥 =
𝑛−3
𝑛−2 0
𝜋
2 sin𝑛−4
𝑥 𝑑𝑥 -------- (2)
Using (2) in (1)
0
𝜋
2 sin𝑛
𝑥 𝑑𝑥 =
𝑛−1
𝑛
𝑛−3
𝑛−2 0
𝜋
2 sin𝑛−4
𝑥 𝑑𝑥
Proceeding like this, we will get
0
𝜋
2 sin𝑛
𝑥 𝑑𝑥 =
𝑛−1
𝑛
𝑛−3
𝑛−2
𝑛−5
𝑛−4
… 0
𝜋
2 sin𝑛−2
𝑥 𝑑𝑥 ------- (3)

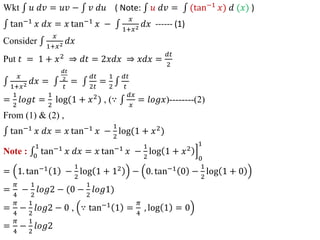
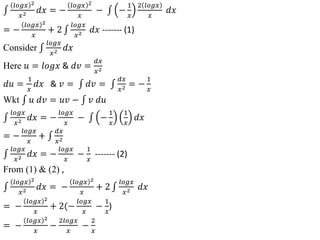
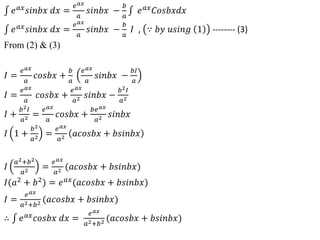
93. If 𝑛 is even ((i.e) 𝑛 = 2), the last integral in (3), 0
𝜋
2 sin𝑛−2
𝑥 𝑑𝑥 becomes
0
𝜋
2 sin𝑛−2
𝑥 𝑑𝑥 = 0
𝜋
2 sin2−2
𝑥 𝑑𝑥 = 0
𝜋
2 sin0
𝑥 𝑑𝑥 = 0
𝜋
2 𝑑𝑥
= ]
𝑥 0
𝜋
2
=
𝜋
2
− 0 =
𝜋
2
------ (4)
If 𝑛 is odd ((i.e) 𝑛 = 3), the last integral in (3) , 0
𝜋
2 sin𝑛−2
𝑥 𝑑𝑥 becomes
0
𝜋
2 sin𝑛−2
𝑥 𝑑𝑥 = 0
𝜋
2 sin3−2
𝑥 𝑑𝑥 = 0
𝜋
2 sin 𝑥 𝑑𝑥
= ]
−𝑐𝑜𝑠𝑥 0
𝜋
2
= −𝑐𝑜𝑠
𝜋
2
− −𝑐𝑜𝑠0 = 0 + 1 = 1, (∵ cos
𝜋
2
= 0 , 𝑐𝑜𝑠0 = 1) ----(5)
Using (4) & (5) in (3)
0
𝜋
2 sin𝑛
𝑥 𝑑𝑥 =
𝑛−1
𝑛
𝑛−3
𝑛−2
𝑛−5
𝑛−4
…
1
2
𝜋
2
, 𝑖𝑓 𝑛 𝑖𝑠 𝑒𝑣𝑒𝑛
𝑛−1
𝑛
𝑛−3
𝑛−2
𝑛−5
𝑛−4
…
2
3
. 1, 𝑖𝑓 𝑛 𝑖𝑠 𝑜𝑑𝑑
Problem 2 : Establish the reduction formula for 𝒄𝒐𝒔𝒏
𝒙 𝒅𝒙
Hence find 𝟎
𝝅
𝟐 𝒄𝒐𝒔𝒏
𝒙 𝒅𝒙
Solution:
Proceed like as per problem 1

94. Problem 3: Find 𝟎
𝝅
𝟐 𝐬𝐢𝐧𝟔
𝒙 𝒅𝒙
Solution:
Wkt 0
𝜋
2 sin𝑛
𝑥 𝑑𝑥 =
𝑛−1
𝑛
𝑛−3
𝑛−2
𝑛−5
𝑛−4
…
1
2
𝜋
2
, 𝑖𝑓 𝑛 𝑖𝑠 𝑒𝑣𝑒𝑛
𝑛−1
𝑛
𝑛−3
𝑛−2
𝑛−5
𝑛−4
…
2
3
. 1, 𝑖𝑓 𝑛 𝑖𝑠 𝑜𝑑𝑑
Here 𝑛 = 6 is even
0
𝜋
2 sin6
𝑥 𝑑𝑥 =
6−1
6
6−3
6−2
6−5
6−4
𝜋
2
=
5
6
3
4
1
2
𝜋
2
=
5𝜋
32
Problem 4: Find 𝟎
𝝅
𝟐 𝐬𝐢𝐧𝟕
𝒙 𝒅𝒙
Solution:
Wkt 0
𝜋
2 sin𝑛
𝑥 𝑑𝑥 =
𝑛−1
𝑛
𝑛−3
𝑛−2
𝑛−5
𝑛−4
…
1
2
𝜋
2
, 𝑖𝑓 𝑛 𝑖𝑠 𝑒𝑣𝑒𝑛
𝑛−1
𝑛
𝑛−3
𝑛−2
𝑛−5
𝑛−4
…
2
3
. 1, 𝑖𝑓 𝑛 𝑖𝑠 𝑜𝑑𝑑
Here 𝑛 = 7 is odd
0
𝜋
2 sin7
𝑥 𝑑𝑥 =
7−1
7
7−3
7−2
7−5
7−4
. 1 =
6
7
4
5
2
3
1 =
48
105

95. Problem 5: Find 𝟎
𝝅
𝟐 𝐜𝐨𝐬𝟖
𝒙 𝒅𝒙
Solution:
Wkt 0
𝜋
2 cos𝑛
𝑥 𝑑𝑥 =
𝑛−1
𝑛
𝑛−3
𝑛−2
𝑛−5
𝑛−4
…
1
2
𝜋
2
, 𝑖𝑓 𝑛 𝑖𝑠 𝑒𝑣𝑒𝑛
𝑛−1
𝑛
𝑛−3
𝑛−2
𝑛−5
𝑛−4
…
2
3
. 1, 𝑖𝑓 𝑛 𝑖𝑠 𝑜𝑑𝑑
Here 𝑛 = 8 is even
0
𝜋
2 cos8
𝑥 𝑑𝑥 =
8−1
8
8−3
8−2
8−5
8−4
.
8−7
8−6
𝜋
2
=
7
8
5
6
3
4
1
2
𝜋
2
=
35𝜋
256
Problem 6: Find 𝟎
𝝅
𝟐 𝐬𝐢𝐧𝟔
𝒙 𝐜𝐨𝐬𝟓
𝒙 𝒅𝒙
Solution:
Wkt 0
𝜋
2 sin𝑚
𝑥 cos𝑛
𝑥 𝑑𝑥 =
𝑛−1
𝑚+𝑛
𝑛−3
𝑚+𝑛−2
…
2
𝑚+3
1
𝑚+1
, 𝑖𝑓 𝑛 𝑖𝑠 𝑜𝑑𝑑
𝑛−1
𝑚+𝑛
𝑛−3
𝑚+𝑛−2
…
1
𝑚+2
𝑚−1
𝑚
𝑚−3
𝑚−2
…
1
2
𝜋
2
, 𝑖𝑓 𝑛 𝑖𝑠 𝑒𝑣𝑒𝑛
Here 𝑚 = 6 & 𝑛 = 5
Also 𝑛 = 5 is odd
0
𝜋
2 sin6
𝑥 cos5
𝑥 𝑑𝑥 =
5−1
6+5
5−3
6+5−2
1
6+1
=
4
11
2
9
1
7
=
8
693

96. Convergent (or) Divergent of Improper Integral
If the limit of integration of the improper integral exists & finite, then the integral
is converges.
If the limit of integration does not exist , then the improper integral is said
to diverge.
Rules:
1. If 𝑎
∞
𝑓 𝑥 𝑑𝑥 = lim
𝑡→∞ 𝑎
𝑡
𝑓 𝑥 𝑑𝑥 is exists and finite, then 𝑎
∞
𝑓 𝑥 𝑑𝑥 is
convergent.
2. If −∞
𝑏
𝑓 𝑥 𝑑𝑥 = lim
𝑡→−∞ 𝑡
𝑏
𝑓 𝑥 𝑑𝑥is exists and finite, then ∞
𝑏
𝑓 𝑥 𝑑𝑥 is
convergent.
3. In both cases the limit does not exists , then the integral is divergent.
Note : For 𝑎 > 0,
𝑎
∞ 1
𝑥𝑝 𝑑𝑥 is convergent if 𝑝 > 1 and divergent if 𝑝 ≤ 1

97. Problem 1: Evaluate 𝟏
∞ 𝟏
𝒙
𝒅𝒙 and determine whether it is convergent or divergent
Solution:
1
∞ 1
𝑥
𝑑𝑥 = lim
𝑡→∞ 1
𝑡 1
𝑥
𝑑𝑥 = lim
𝑡→∞
]
𝑙𝑜𝑔𝑥 1
𝑡
= lim
𝑡→∞
𝑙𝑜𝑔𝑡 − 𝑙𝑜𝑔1 = lim
𝑡→∞
𝑙𝑜𝑔𝑡 = ∞
∴The given integral is divergent.
Problem 2: Evaluate 𝟑
∞ 𝒅𝒙
𝒙−𝟐
𝟑
𝟐
and determine whether it is convergent or divergent
Solution:
3
∞ 𝑑𝑥
𝑥−2
3
2
= lim
𝑡→∞ 3
𝑡 𝑑𝑥
𝑥−2
3
2
= lim
𝑡→∞ 3
𝑡
𝑥 − 2 −
3
2𝑑𝑥
= lim
𝑡→∞
𝑥−2
−
3
2
+1
−
3
2
+1
3
𝑡
∵ 𝑎𝑥 ± 𝑏 𝑛
𝑑𝑥 =
𝑎𝑥±𝑏 𝑛+1
𝑛+1
= lim
𝑡→∞
𝑥−2
−
1
2
−
1
2 3
𝑡
=lim
𝑡→∞
−2 𝑥 − 2 −
1
2
3
𝑡
= lim
𝑡→∞
− 2 𝑡 − 2 −
1
2 − (−2 3 − 2 −
1
2)
= lim
𝑡→∞
−
2
𝑡−2
1
2
+ 2 = −
2
∞
+ 2 = 0 + 2 = 2
Hence the given integral is convergent

98. Problem 3: Evaluate 𝟎
𝟑 𝟏
𝟗−𝒙𝟐
𝒅𝒙 and determine whether it is convergent or
divergent
Solution:
0
3 1
9−𝑥2
𝑑𝑥 = 𝑆𝑖𝑛−1 𝑥
3 0
3
, ∵
𝑑𝑥
𝑎2−𝑥2
= sin−1 𝑥
𝑎
, ℎ𝑒𝑟𝑒 𝑎 = 3
= 𝑆𝑖𝑛−1 3
3
− Sin−1
0
= 𝑆𝑖𝑛−1
1 − 𝑆𝑖𝑛−1
0
=
𝜋
2
− 0 ∵ 𝑆𝑖𝑛−1
1 =
𝜋
2
, 𝑆𝑖𝑛−1
0 = 0
=
𝜋
2
∴ the given integral is convergent.
Problem 4: Evaluate 𝟐
𝟑 𝟏
𝟑−𝒙
𝒅𝒙 and determine whether it is convergent or
divergent
Solution:
2
3 1
3−𝑥
𝑑𝑥 = 2
3
3 − 𝑥 −
1
2𝑑𝑥

99. =
3−𝑥
−
1
2
+1
(−
1
2
+1)(−1)
2
3
, ∵ 𝑏 − 𝑎𝑥 𝑛
𝑑𝑥 =
𝑏−𝑎𝑥 𝑛+1
−𝑎 𝑛+1
, ℎ𝑒𝑟𝑒 𝑎 = −1, 𝑏 = 3
=
3−𝑥
1
2
−
1
2 2
3
= −2 3 − 𝑥
1
2
2
3
= −2 3 − 3
1
2 − −2 3 − 2
1
2
= 0 + 2 = 2
Hence the given integral is convergent.
Problem 5: Evaluate 𝟒
∞ 𝟏
𝒙
𝒅𝒙 and determine whether it is convergent or
divergent
Solution:
4
∞ 1
𝑥
𝑑𝑥 = lim
𝑡→∞ 4
𝑡
𝑥−
1
2𝑑𝑥 = lim
𝑡→∞
𝑥
−
1
2
+1
−
1
2
+1
4
𝑡
= lim
𝑡→∞
𝑥
1
2
1
2 4
𝑡
= lim
𝑡→∞
2𝑥
1
2
4
𝑡
= lim
𝑡→∞
2 𝑡
1
2 − 4
1
2 = 2lim
𝑡→∞
𝑡
1
2 − 2 2 = ∞
Hence the given integral is divergent.

100. Problem 6: Evaluate 𝟏
∞ 𝟏
𝒙𝟐 𝒅𝒙 and determine whether it is convergent or
divergent.
Solution:
1
∞ 1
𝑥2 𝑑𝑥 = lim
𝑡→∞ 1
𝑡 1
𝑥2 𝑑𝑥 = lim
𝑡→∞
−
1
𝑥 1
𝑡
= lim
𝑡→∞
−
1
𝑡
− −
1
1
= − lim
𝑡→∞
1
𝑡
+ 1
= −
1
∞
+ 1 = 0 + 1 = 1
Hence the given integral is convergent
Problem 7: Evaluate 𝟎
∞
𝒆−𝒙 𝒅𝒙 and determine whether it is convergent or
divergent.
Solution:
0
∞
𝑒−𝑥
𝑑𝑥 = lim
𝑡→∞ 0
𝑡
𝑒−𝑥
𝑑𝑥 = lim
𝑡→∞
𝑒−𝑥
−1 0
𝑡
= lim
𝑡→∞
−𝑒−𝑡
− −𝑒0
= − lim e−t + 1
𝑡→∞
= −𝑒−∞ + 1 = 0 + 1 = 1 , (∵ 𝑒−∞ = 0)
Hence the given integral is convergent

101. Problem 8: Evaluate 𝟏
∞ 𝟏
𝒂𝟐+𝒙𝟐 𝒅𝒙 and determine whether it is convergent or
divergent
Solution:
1
∞ 1
𝑎2+𝑥2 𝑑𝑥 = lim
𝑡→∞ 1
𝑡 1
𝑎2+𝑥2 𝑑𝑥 = lim
𝑡→∞
1
𝑎
tan−1 𝑥
𝑎 1
𝑡
=
1
𝑎
lim
𝑡→∞
tan−1 𝑡
𝑎
− tan−1
1
=
1
𝑎
(tan−1
∞ −
𝜋
4
) =
1
𝑎
𝜋
2
−
𝜋
4
(∵ tan−1
1 =
𝜋
4
, tan−1
∞ =
𝜋
2
)
=
1
𝑎
𝜋
2
=
𝜋
2𝑎
Hence the given integral is convergent
Problem 9: Evaluate −∞
𝟎
𝒆𝒙
𝒅𝒙 and determine whether it is convergent or
divergent.
Solution:
−∞
0
𝑒𝑥
𝑑𝑥 = lim
𝑡→−∞ 𝑡
0
𝑒𝑥
𝑑𝑥 = lim
𝑡→−∞
]
𝑒𝑥
𝑡
0
= lim
𝑡→−∞
(𝑒0
− 𝑒𝑡
)
= lim
𝑡→−∞
1 − 𝑒𝑡 = 1 − lim
𝑡→−∞
𝑒𝑡 = 1 − 𝑒−∞ = 1 − 0 = 1
Hence the given integral is convergent

102. Theorem : (𝒑 - test) Prove that For 𝒂 > 𝟎, 𝒂
∞ 𝟏
𝒙𝒑 𝒅𝒙 is convergent if 𝒑 > 𝟏 and
divergent if 𝒑 ≤ 𝟏
Proof:
𝑎
∞ 1
𝑥𝑝 𝑑𝑥 = lim
𝑡→∞ 𝑎
𝑡 𝑑𝑥
𝑥𝑝 = lim
𝑡→∞ 𝑎
𝑡
𝑥−𝑝
𝑑𝑥 = lim
𝑡→∞
𝑥−𝑝+1
−𝑝+1 𝑎
𝑡
𝑎
∞ 1
𝑥𝑝 𝑑𝑥 =
1
1−𝑝
lim
𝑡→∞
𝑡1−𝑝
− 𝑎1−𝑝
-------- (1)
Case I: If 𝑝 > 1
Consider lim
𝑡→∞
𝑡1−𝑝
=
1
∞
= 0
Hence from (1), 𝑎
∞ 1
𝑥𝑝 𝑑𝑥 is convergent.
Case II: If 𝑝 < 1
Consider lim
𝑡→∞
𝑡1−𝑝
= ∞
Hence from (1), 𝑎
∞ 1
𝑥𝑝 𝑑𝑥 is divergent.
Case III: If 𝑝 = 1
Consider
1
1−𝑝
=
1
0
= ∞
Hence from (1), 𝑎
∞ 1
𝑥𝑝 𝑑𝑥 is divergent.