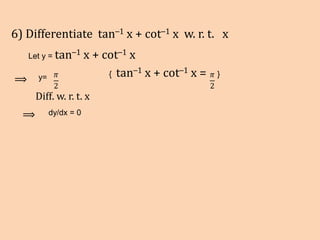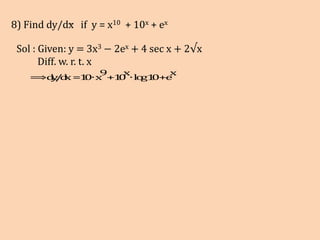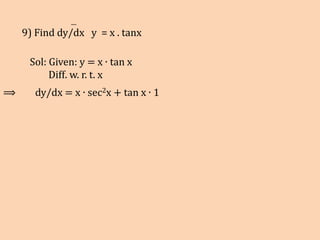1) The document contains solutions to 10 calculus problems involving finding derivatives and evaluating functions. The problems include finding derivatives of trigonometric, logarithmic, and exponential functions, as well as evaluating functions at given values. 2) The solutions show the steps taken to solve each problem through substitution and application of derivative rules. 3) The techniques demonstrated include finding derivatives using basic rules, evaluating functions by substitution, and simplifying expressions involving trigonometric identities.

1. ASSIGNMENT 1

2. 1) If f(x) = x3 − 3x2 + 5, find f(0) + f(3).
Sol:
∴
f(0) = (0)3 − 3(0)2 +
5
by substituting x = 0
⟹ f(0) = 5
Also
,
f(3) = (3)3 − 3(3)2 +
5
by substituting x = 3
⟹ f(3) = 27 − 27 + 5
⟹ f(3) = 5
∴ f(0) + f(3) = 5 + 5
⟹ f(0) + f(3) = 10

3. 2) If f(x) = tan–1 x , find f(1)
4
Sol: Given: f(x) = tan–1 x
 f(1) = tan–1(1) by substituting x =1
⟹ f(1) =
4
4


4. Sol: Given: f(x) = x3 − 3x + sin x
Consider f(−x) = (−x)3 − 3(−x) + sin(−x)
⟹ f(−x) = − x3 + 3x − sin x
⟹ f(−x) = −{ x3 − 3x + sin x }
⟹ f(−x) = −f(x)
⟹ f(x) is an odd function.
3) State with proof whether the function f(x) = x3 − 3x +sinx
is even or odd

5. Sol : Given: f(x) = 3x4 + x2 + 5 − 3 cos x + 2sin2x …….. (i)
Consider f(−x) = 3(−x)4 + (−x)2 + 5 − 3 cos(−x) + 2sin2(−x)
= 3x4 + x2 + 5 − 3 cos x + 2sin2x
{sin(−θ) = − sin θ and cos (−θ) = cos θ}
⟹ f(− x) = f(x) from ( i)
4) If f(x) = 3x4 + x2 + 5 − 3 cos x + 2sin2x . Show that f(x) + f(−x) = 2f(x)

6. 5) If f(x) = = log(√1 + x2 + x) , find f(x) + f(− x)
Sol: Given: f(x) = log(√1 + x2 + x)
x
1
f(x) + f(− x) = log √1 + x + x + log(√1 +( - ) + (-x) )
⟹ f(x) + f(− x) = log √1 + + x + log √1 + x − x
⟹ f(x) + f(− x) = log √1 + x + x ∙ √1 + x − x
1 + (− x) + (− x)
𝑥2
⟹ f(x) + f(− x) = log 1 + x − x
⟹ (a + b)(a − b) = a − b
f(x) + f(− x) = log(1)
⟹ log + log
f(x) + f(− x) = 0

7. 6) Differentiate tan–1 x + cot–1 x w. r. t. x
Let y = tan–1 x + cot–1 x
y= 𝜋
2
{ tan–1 x + cot–1 x = }
Diff. w. r. t. x
dy/dx = 0⟹
⟹
𝜋
2

8. 7)Find dy/dx if y = 4 sin x − 8 cos x + tan x – sec x
Sol: Given: y = 4 sin x − 8 cos x + tan x − sec x
Diff. w. r. t. x
⟹ dy/dx = 4 cos x − 8(− sin x) + sec2 x − sec x tan x
⟹ dy/dx = 4 cos x + 8 sin x + sec2 x − sec x tan x

9. 8) Find dy/dx if y = x10 + 10x + ex
Sol : Given: y = 3x3 − 2ex + 4 sec x + 2√x
Diff. w. r. t. x
⟹dy/dx=10∙x
9
+10
x
∙log10+e
x

10. 9) Find dy/dx y = x . tanx
Sol: Given: y = x ∙ tan x
Diff. w. r. t. x
⟹ dy/dx = x ∙ sec2x + tan x ∙ 1

11. 10) Find dy/dx if y = (x + 1). log(x)
Sol : Given: y = (x + 1). log(x)
Diff. w. r. t. x
dy/dx = (x+1) . + log (x)
x
1