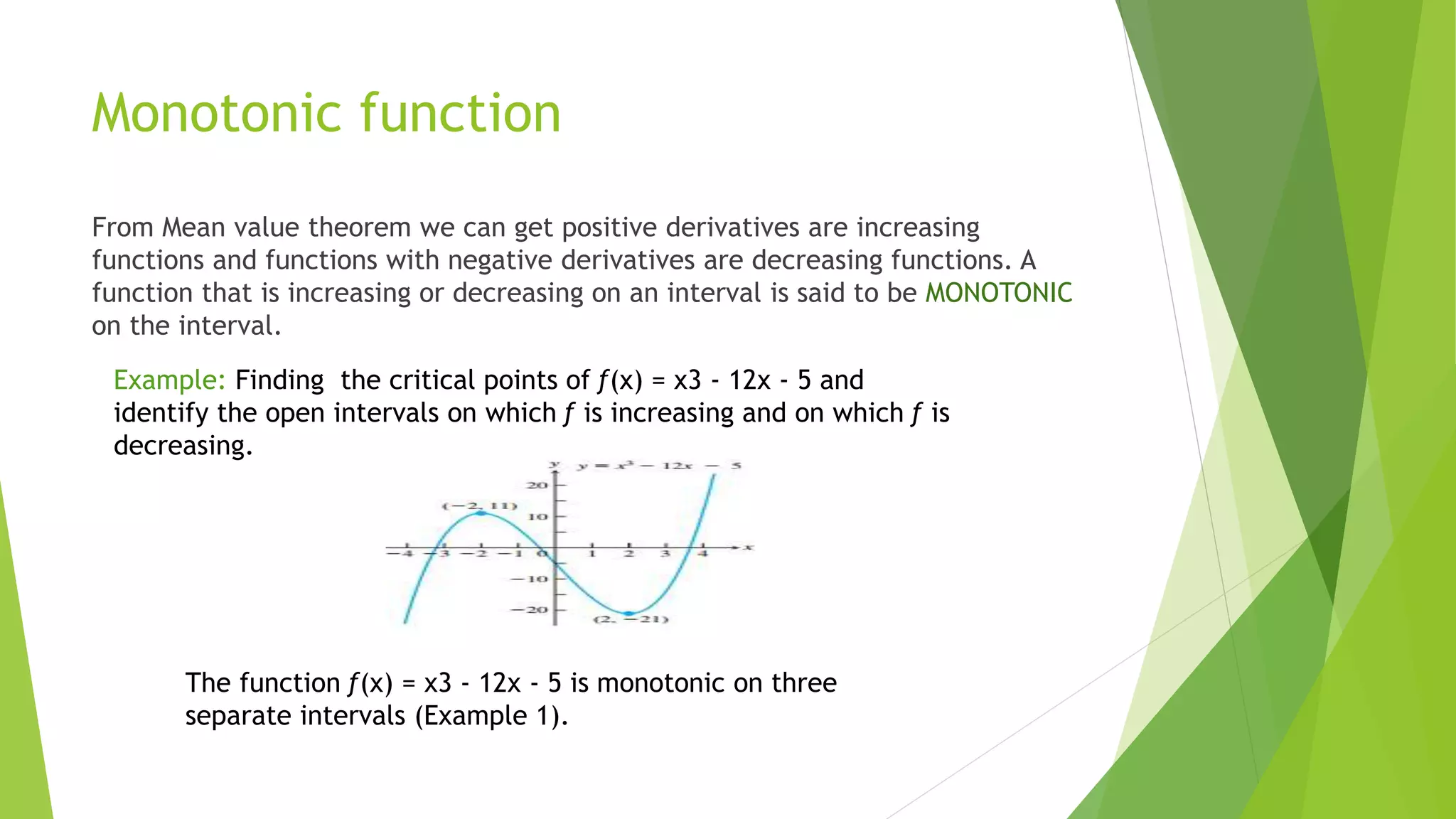
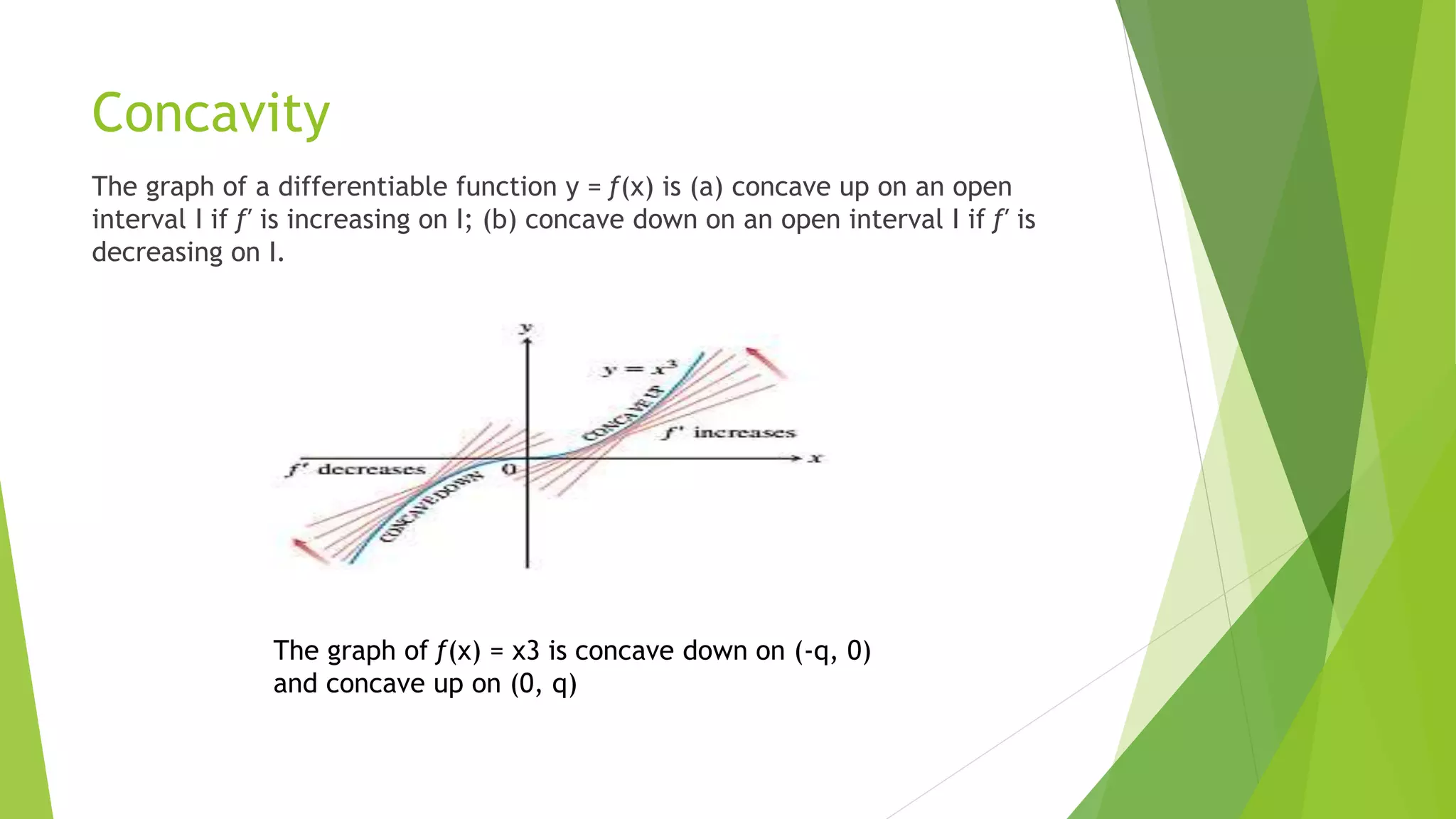
This presentation discusses applications of derivatives including: extreme values of functions, the mean value theorem, monotonic functions, and concavity. It defines maximum and minimum values and explains how the mean value theorem states that between two points a and b on a continuous function, there exists a point c where the slope of the tangent line is equal to the slope of the secant line between a and b. Monotonic functions are defined as increasing or decreasing functions based on the mean value theorem. Concavity is defined based on whether the derivative of a function is increasing or decreasing, which determines if the graph is concave up or down.

1. Presented By
Abdullah Al Mamun
PRESENTATION ON
MATHEMATICS -III

2. Applications of Derivative
 Extreme values of function.
 The mean value theorem.
 Monotonic function.
 Concavity.

3. Extreme values of function
Let ƒ be a function with domain D.
Then ƒ has an absolute maximum
value on D at a point c if ƒ(x) … ƒ(c)
for all x in D and an absolute
minimum value on D at c if ƒ(x) Ú
ƒ(c) for all x in D.
Maximum and minimum values are called extreme values of the
function ƒ. Absolute maxima or minima are also referred to as
global maxima or minima.

4. The mean value theorem.
Suppose y = ƒ(x) is continuous over a closed interval 3a, b4
and differentiable on the interval’s interior (a, b). Then
there is at least one point c in (a, b) at which ƒ(b) - ƒ(a) b - a
= ƒ′(c).
Geometrically, the Mean Value Theorem says that somewhere between a and b
the curve has at least one tangent parallel to the secant joining A and B.

5. Monotonic function
From Mean value theorem we can get positive derivatives are increasing
functions and functions with negative derivatives are decreasing functions. A
function that is increasing or decreasing on an interval is said to be MONOTONIC
on the interval.
Example: Finding the critical points of ƒ(x) = x3 - 12x - 5 and
identify the open intervals on which ƒ is increasing and on which ƒ is
decreasing.
The function ƒ(x) = x3 - 12x - 5 is monotonic on three
separate intervals (Example 1).

6. Concavity
The graph of a differentiable function y = ƒ(x) is (a) concave up on an open
interval I if ƒ′ is increasing on I; (b) concave down on an open interval I if ƒ′ is
decreasing on I.
The graph of ƒ(x) = x3 is concave down on (-q, 0)
and concave up on (0, q)

8. EVERYONE