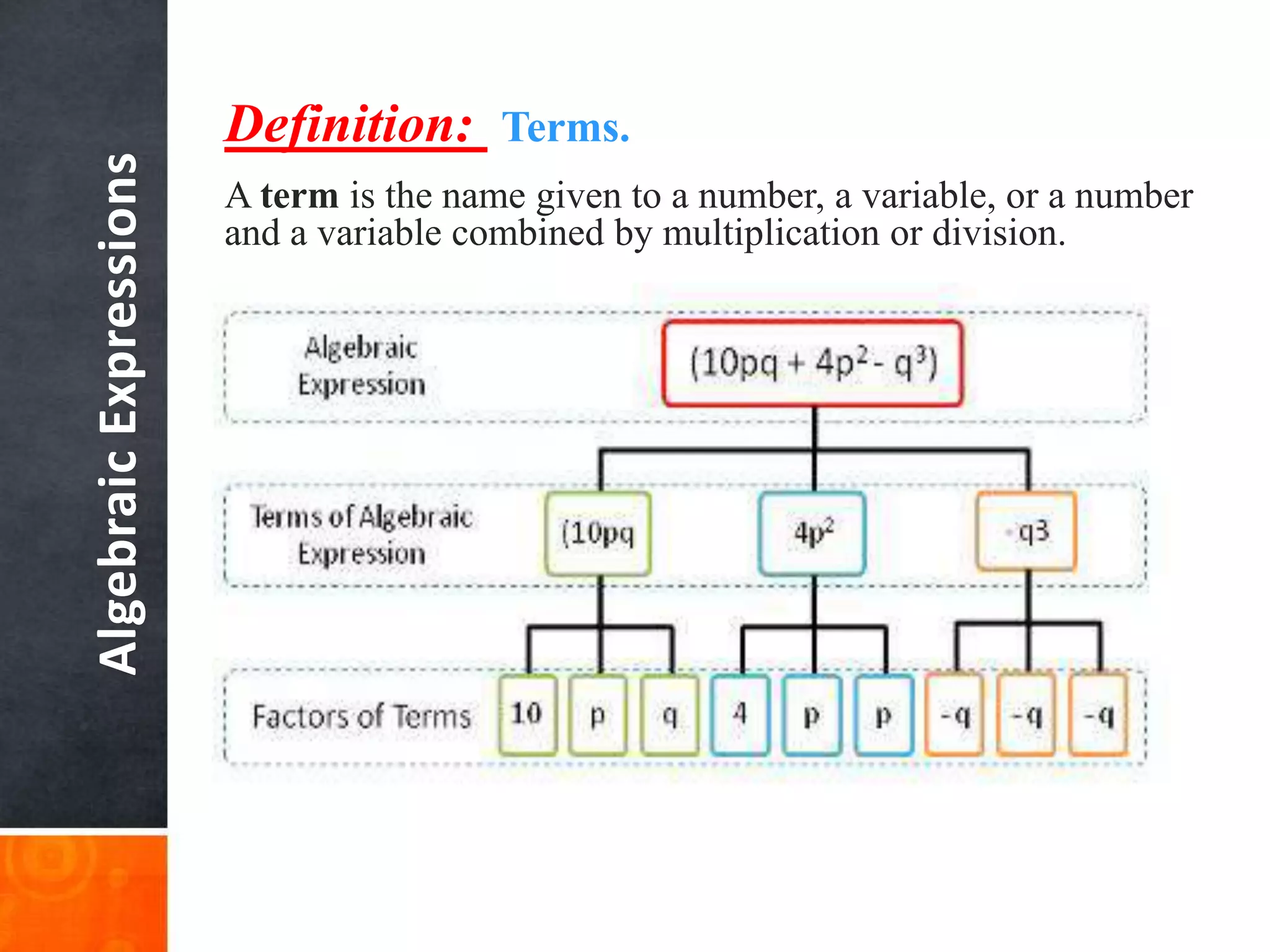
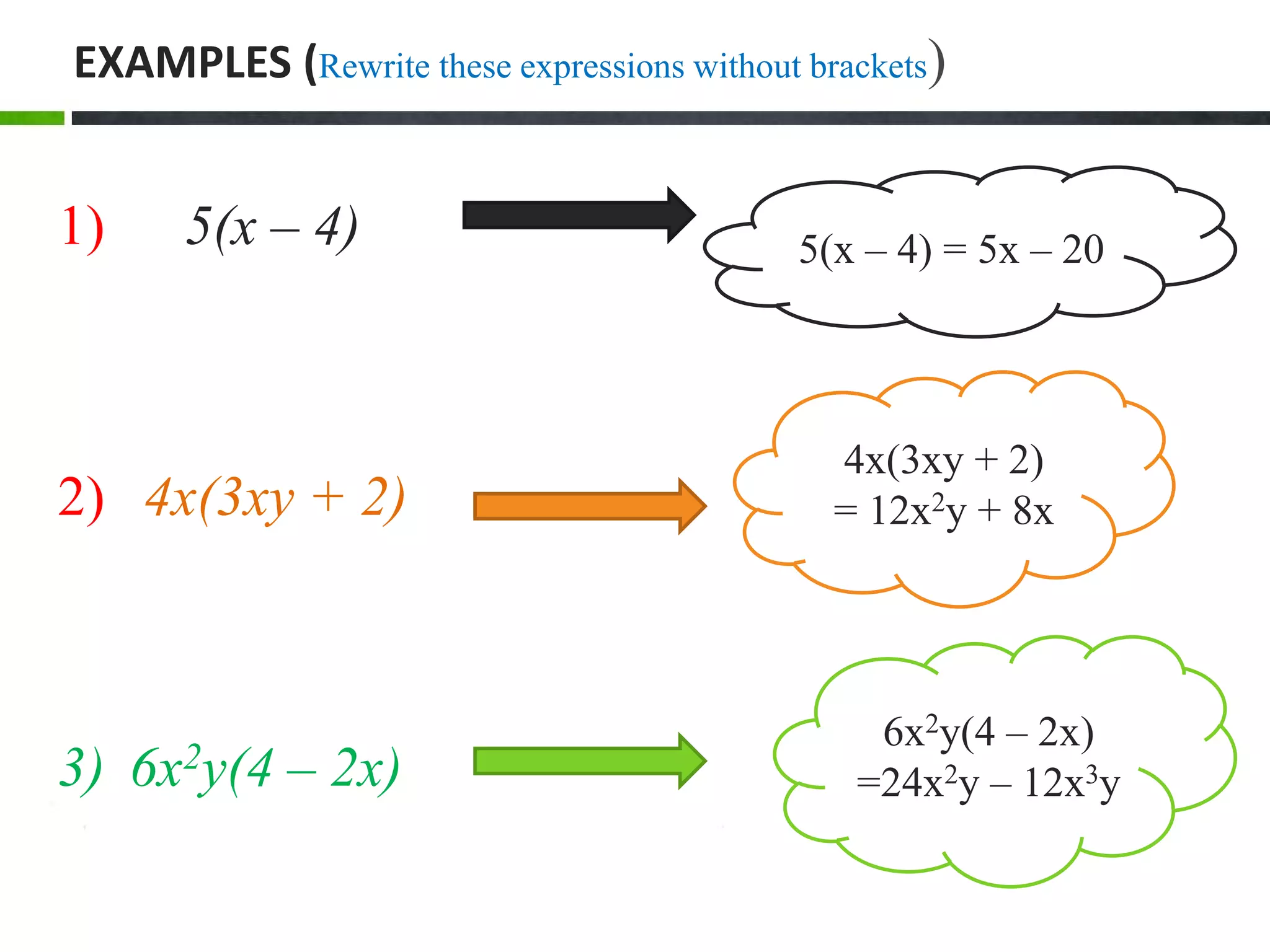
The document outlines the fundamentals of algebraic expressions, including definitions of variables, constants, coefficients, terms, and the operations of addition, subtraction, and multiplication. It highlights the contributions of notable mathematicians like al-Khwarizmi and the significance of algebra in simplifying complex mathematical ideas. Additionally, it provides examples and rules for manipulating algebraic expressions and discusses the historical context of algebra.

1. Algebraic Expression
and Expansion

3. Learning Outcomes
“A star does not compete with other stars around it; it just shines.”
Algebraic
Expressions
Operations Expansions

6. You are familiar with the
following type of numerical
expressions:
12 + 6
3 (12)
6 (3 + 2)
15 -4 (6)

7. Variable
In the expression
12 + B,
the letter “B” is a variable.
A variable is a letter or symbol that represents an
unknown value.

8. Constants
In the expression:
5x + 7y + 2
the constant is 2
In the expression: x -3
the constant is -3
A constant is a number that cannot change its value.

10. Algebraic
Expressions
When variables are used with other numbers,
parentheses, or operations, they create an algebraic
expression.

11. MOTIVATION
Algebra is a fascinating and essential part of mathematics. It provides the
written language in which mathematical ideas are described.
Many parts of mathematics are initiated by finding patterns and relating to
different quantities. Before the introduction and development of algebra, these
patterns and relationships had to be expressed in words. As these patterns and
relationships became more complicated, their verbal descriptions became
harder and harder to understand. Our modern algebraic notation greatly
simplifies this task.

12. MOTIVATION
A well-known formula, due to Einstein, states that
E = mc2 .This remarkable formula gives the relationship
between energy, represented by the letter E, and mass,
represented by letter m. The letter c represents the speed
of light, a constant, which is about 300 000 000 metres
per second.
E = mc2.

13. MOTIVATION
The simple algebraic statement E = mc2 states that some
matter is converted into energy (such as happens in a
nuclear reaction),
then the amount of energy produced is equal to the mass
of the matter multiplied by the square of the speed of
light. You can see how compact the formula is
compared with the verbal description.
E = mc2.

14.  Al-Khwārizmī's contributions
to mathematics, geography,
astronomy.
 He established the basis for
innovation in algebra
and trigonometry.
 His systematic approach to
solving linear and quadratic
equations led to algebra.
Muhammad ibn Musa al-Khwarizmi

15.  A number x is multiplied by itself and then doubled.
 x × x × 2 = x2 × 2 = 2x2.
 A number x is squared and then multiplied by the
square of a second number y.
 x2 × y2 = x2y2.
 A number x is multiplied by a number y and the result
is squared.
 (x × y)2 = (xy)2 which is equal to x2y2
EXAMPLES (concise algebraic notation.)

16. Algebraic
Expressions Definition: Coefficients.
A coefficient is the number multiplied by the variable in an algebraic
expression.

17. Algebraic
Expressions
Definition: Coefficients.

18. Algebraic
Expressions
Definition: Coefficients.

19. Algebraic
Expressions Definition: Terms.
A term is the name given to a number, a variable, or a number
and a variable combined by multiplication or division.

20. Algebraic
Expressions Definition: Like and Unlike Terms.
If you have 3 pencil case with the same number x
of pencils in each,
you have 3x pencils altogether.
x pencils x pencils x pencils

21. Algebraic
Expressions Definition: Like Terms.
If there are 2 more pencil cases with x pencils in
each,
then you have 3x + 2x = 5x pencils altogether.
This can be done as the number of pencils in
each case is the same. The terms 3x and 2x are
said to be like terms.
x pencils x pencils x pencils
x pencils x pencils

22. Terms.
Algebraic
Expressions
Terms
3x + 5y
3m + 6n -6
4x2y -12xy+7x

23. Like and Unlike Terms.
Terms Like
Terms
Unlike
Terms
3x , 5x
4x2 , 8x
4x2y , 12x2y

24. OPERATIONS
“A rose does not answer its enemies with words, but with beauty.”

25. Algebraic
Expressions Addition and Subtraction
Working Rule:
In adding algebraic expressions, we collect
different groups of like terms and find the
sum/difference of like terms.

26. 1) 2x + 3x + 5x
2) 3xy + 2xy
3) 4x2 – 3x2
4) 2x2 + 3x + 4x
5) 4x2y – 3x2y + 3xy2
EXAMPLES (Simplify each of the following by adding or subtracting like terms)
2x + 3x + 5x = 10x
3xy + 2xy = 5xy
4x2 – 3x2 = x2
2x2 + 3x + 4x
= 2x2 + 7x
4x2y – 3 x2 y +3xy2
= x2 y + 3x y2

27. Algebraic
Expressions Multiplication
Working Rule:
3x × 2 y × 2 x y
= 3 × 2 × 2 × x × x × y × y = 12x2y2

28. 1) 5 × 2a
2) 3a × 2a
3) 5xy × 2xy
EXAMPLES (Simplify each of the following)
5 × 2a = 10a
3a × 2a
= 3 × a × 2 × a
=6a2
5xy × 2xy
= 5 × x × y × 2 × x ×
y
= 10x2y2

29. Addition and Subtraction
Algebraic Expression Solution
3x + 5x
4x2 -2x2 +9x
4x2y + 12x2y- 4xy

30. Multiplication
Algebraic Expression Solution
3x × 5x
4x2 × 2x2 × 9x
4x2y × 12x2y × 4xy

31. This process of rewriting
an expression to remove
brackets is usually referred
to as expanding brackets.
EXPANDING
BRACKETS AND
COLLECTING LIKE
TERMS
Expansions of Algebraic Expressions

32. 1) 5(x – 4)
2) 4x(3xy + 2)
3) 6x2y(4 – 2x)
EXAMPLES (Rewrite these expressions without brackets)
5(x – 4) = 5x – 20
4x(3xy + 2)
= 12x2y + 8x
6x2y(4 – 2x)
=24x2y – 12x3y

33. Expansions
Algebraic Expression Solution
3(x + 5)
4x2 ( 2x2 - 9x)
4x2y( 12x + 4xy)

34. HISTOR
Y
But wait…
There’s More!

35. »Descartes (La Geometrie, 1637)
»Wallis (1693)
»Egyptian scribe Ahmes (1650 BC)
»Scottish antiquarian, Henry Rhind (1858 )
»Euclid (circa 300 BC)
»Diophantus (circa 275 AD )
»An Indian mathematician Baudhayana (800 BC)
»The Indian mathematician Brahmagupta (680 AD )
»al-Khwarizmi,(circa 825 AD)
»Fibonacci European writer (circa 1225 AD)
»Cardano, Tartaglia (16th century),
(algebra has a very long history)
Name of mathematician and Countries

36. » A History of Mathematics: An
Introduction, 3rd Edition, Victor
J. Katz, Addison-Wesley, (2008)
REFERENCES

38. What’s Your Message?