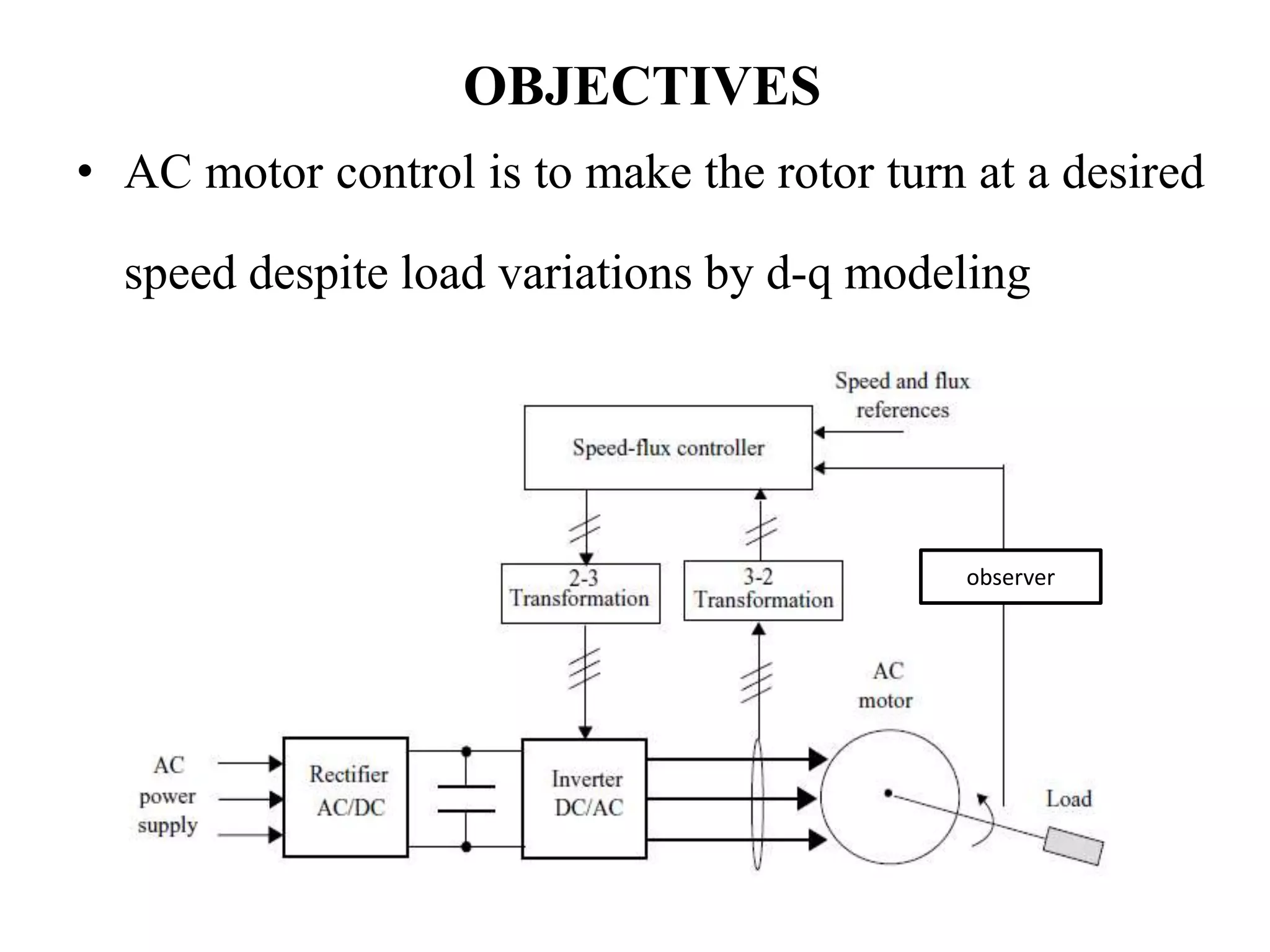
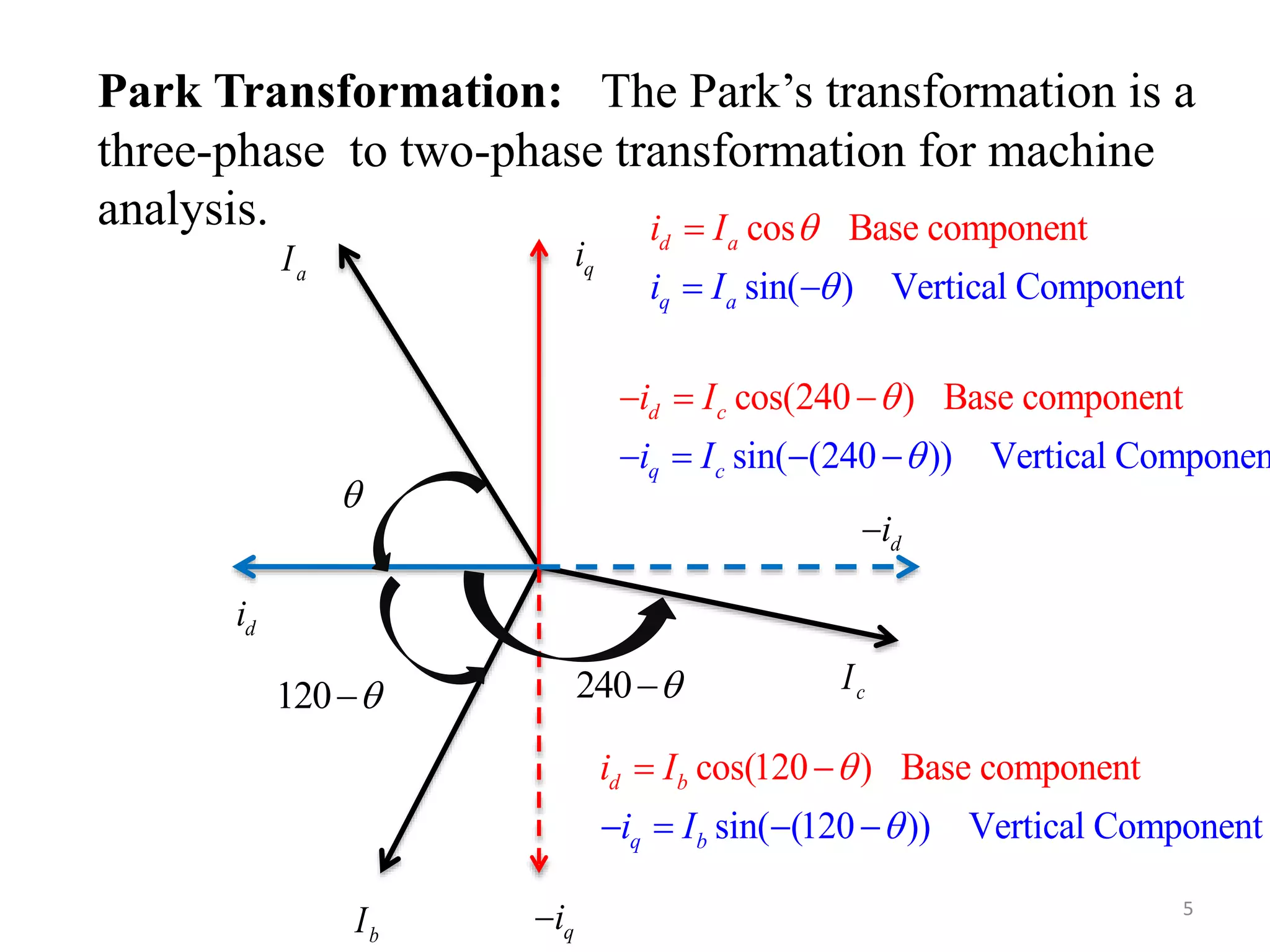
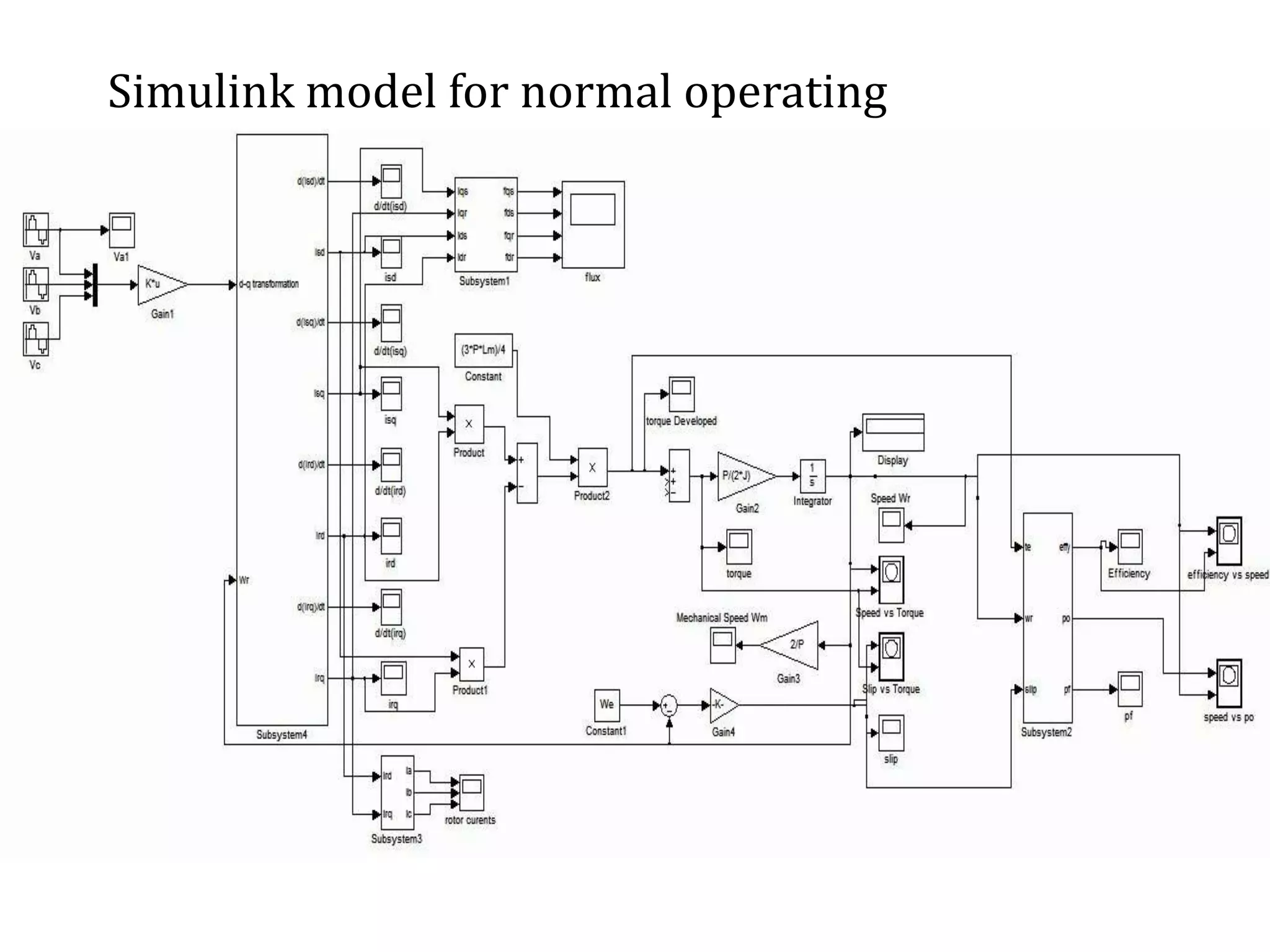
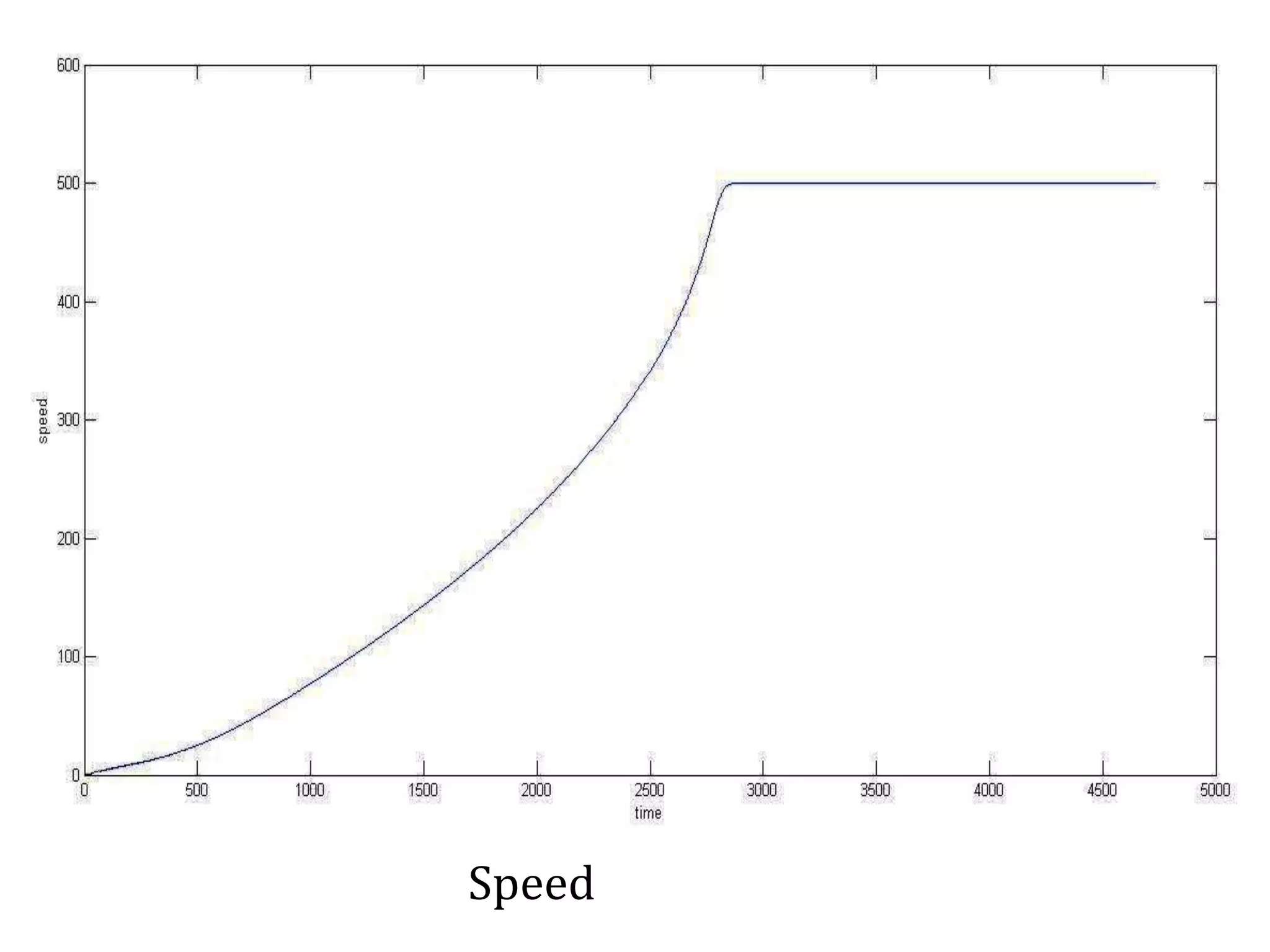
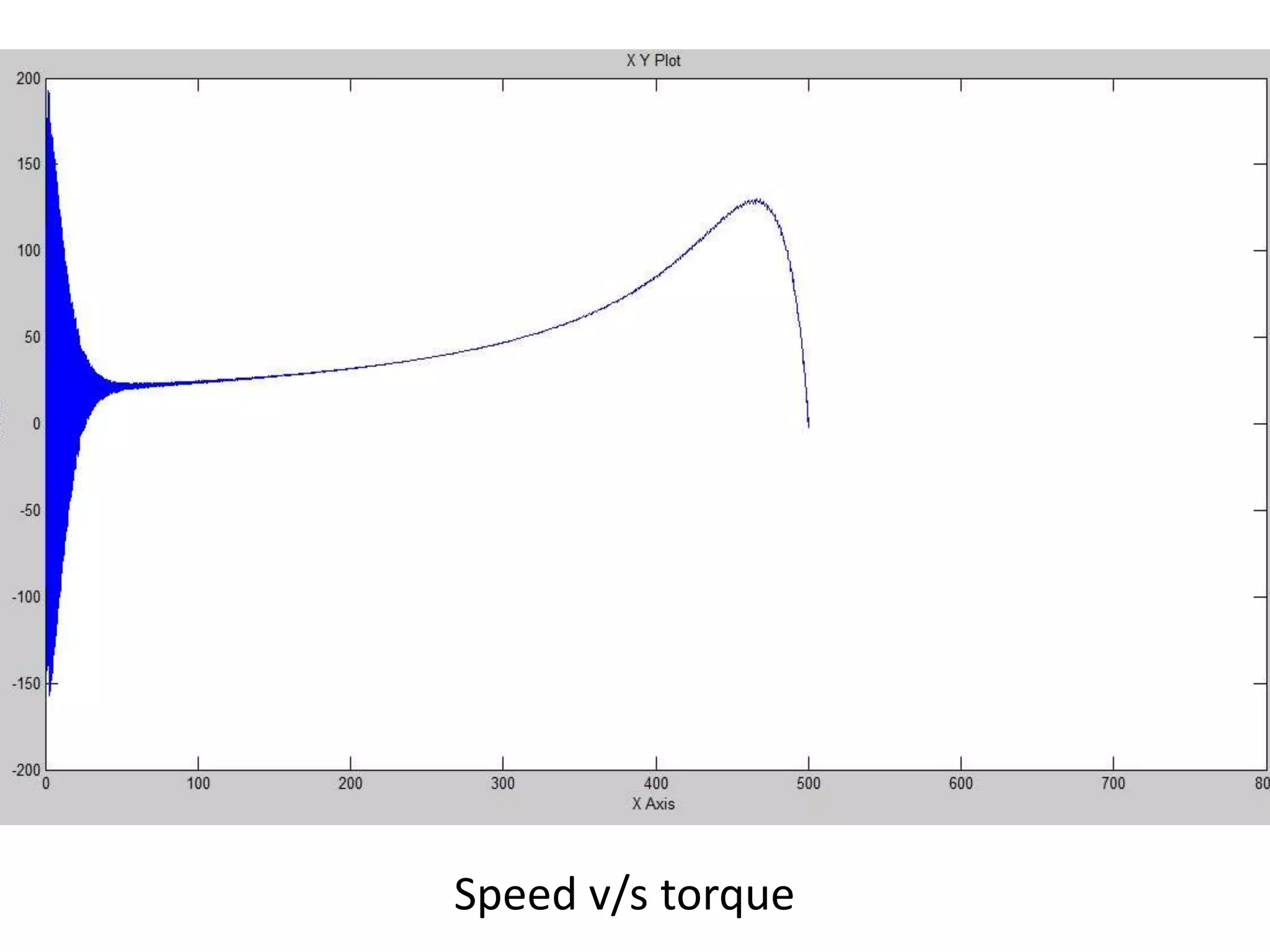
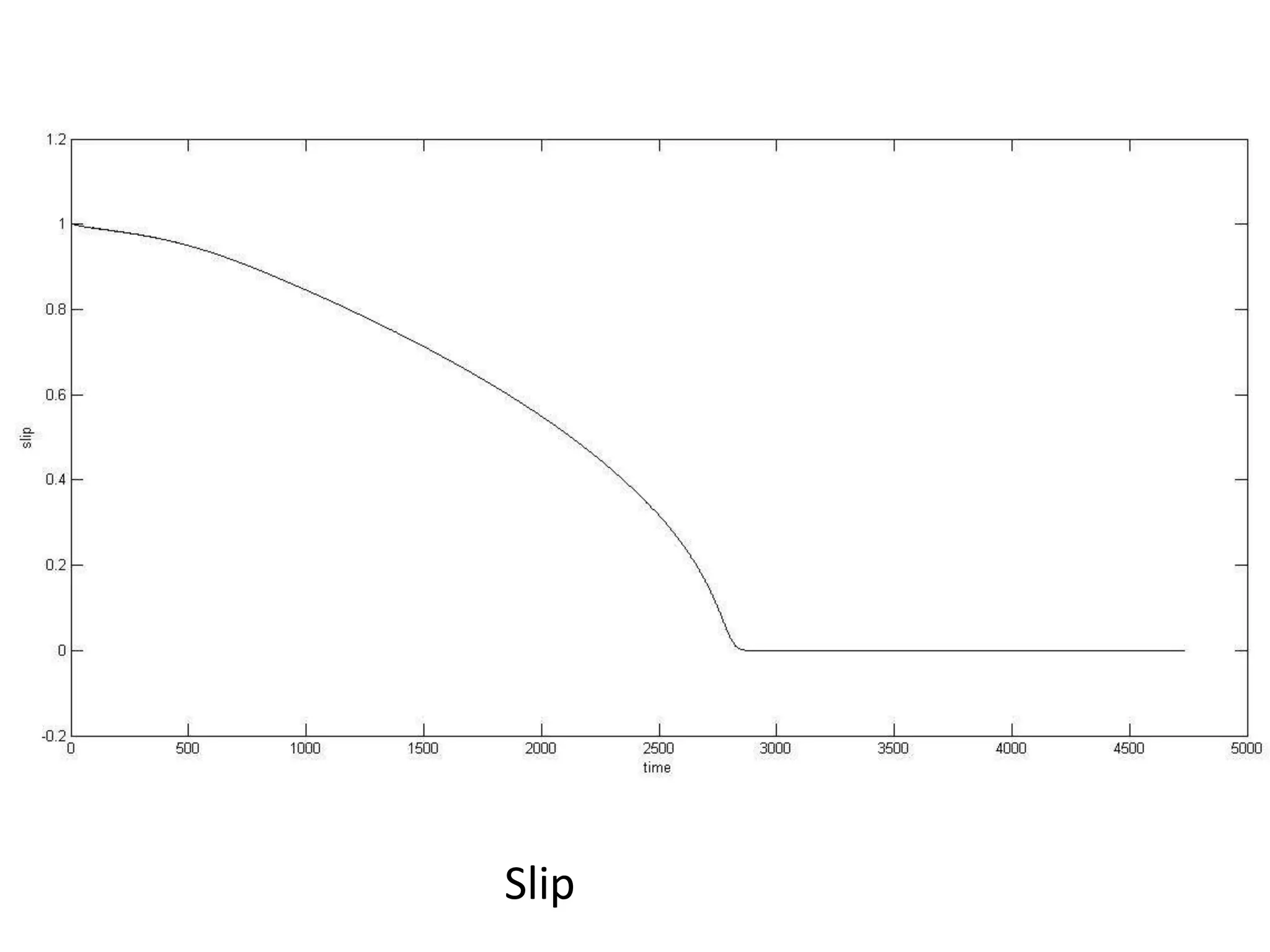
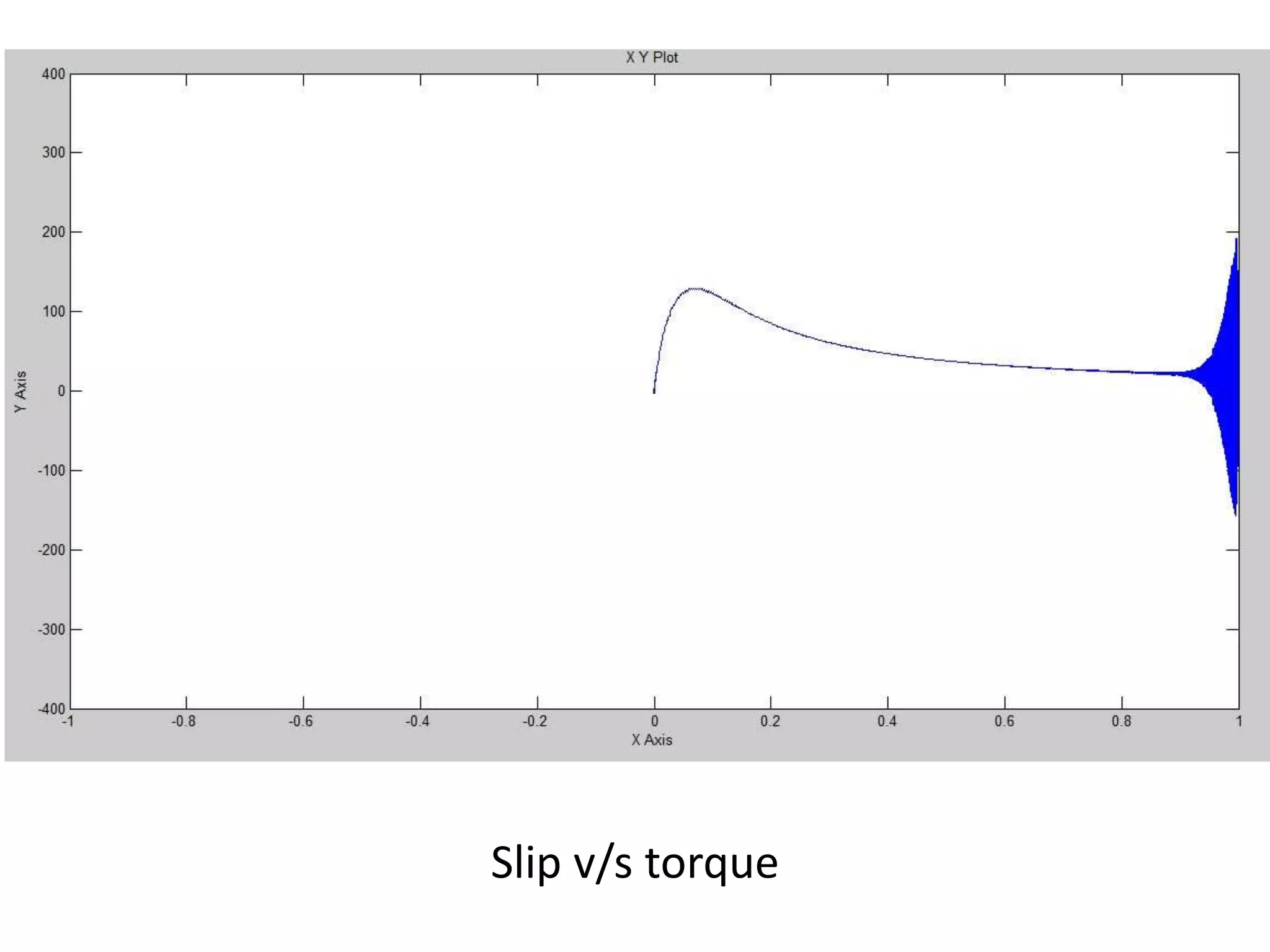
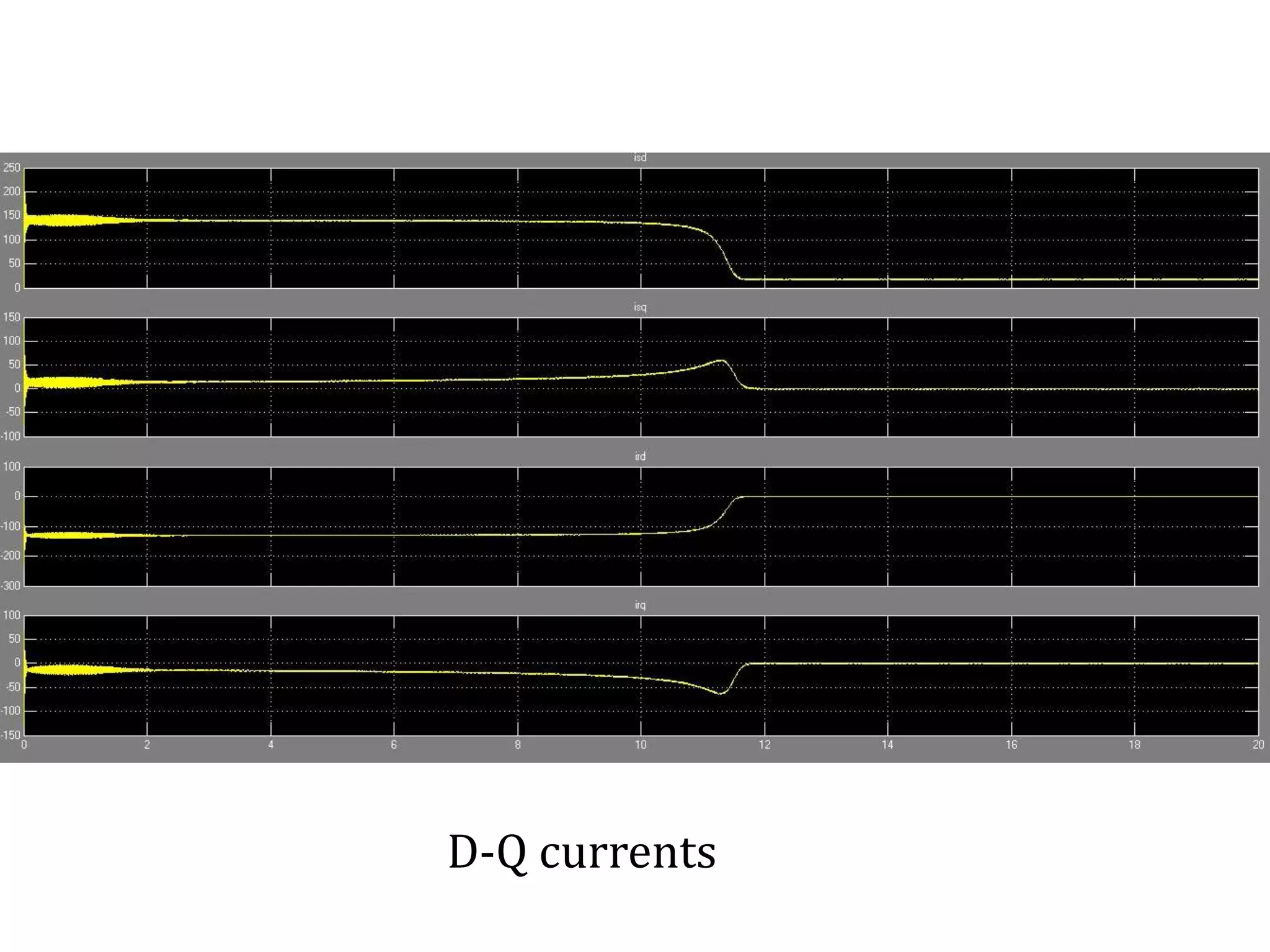
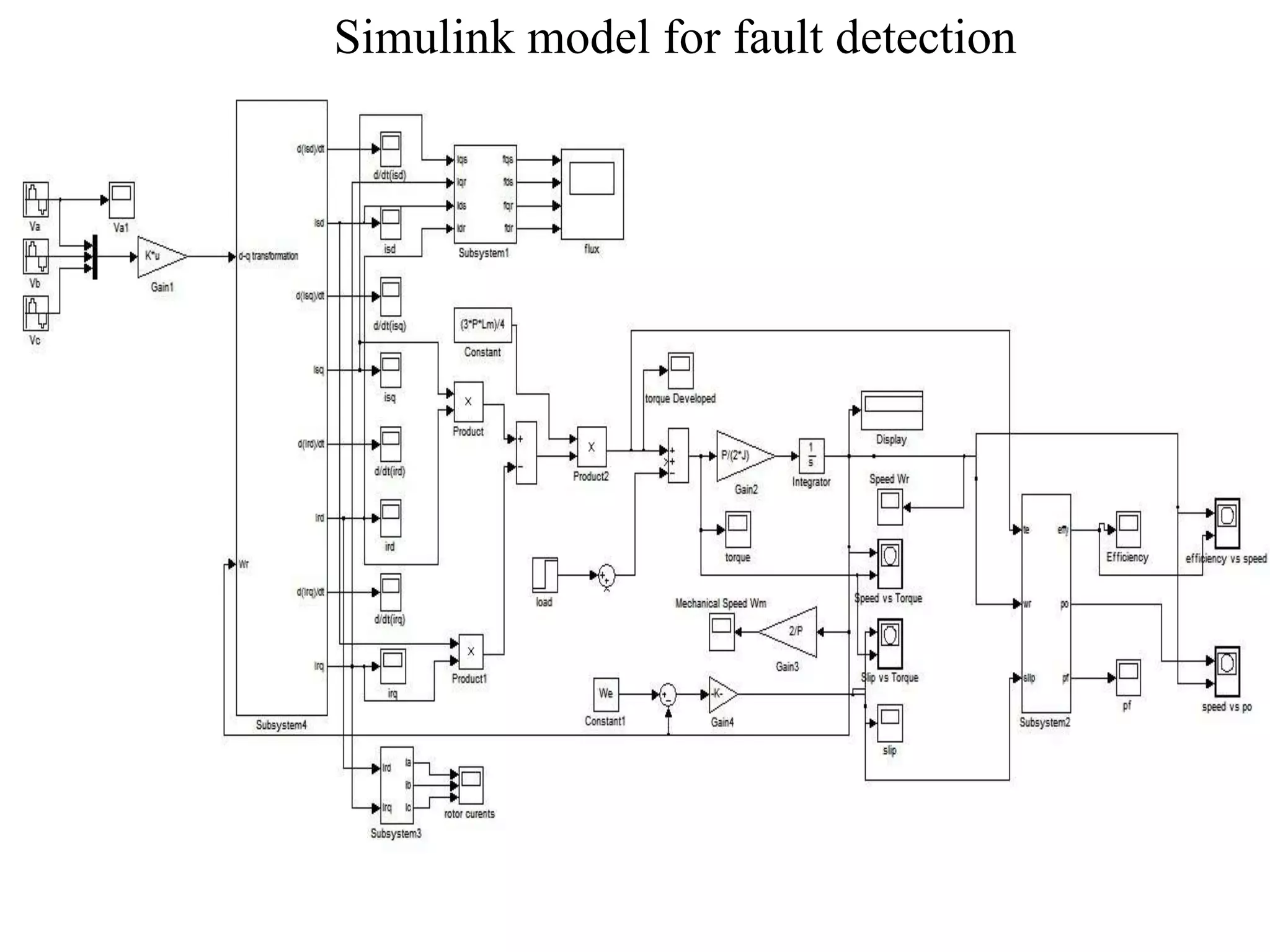
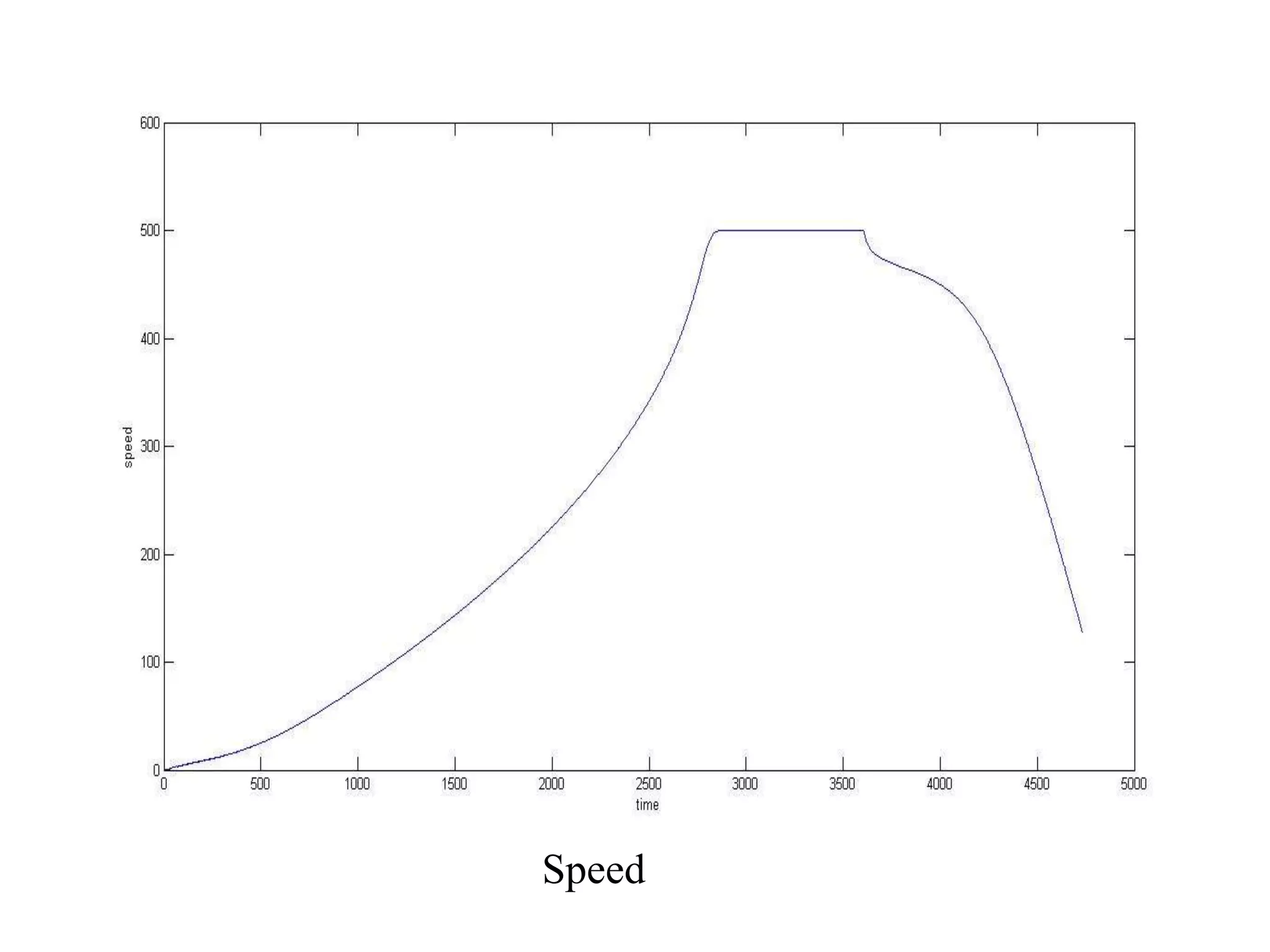
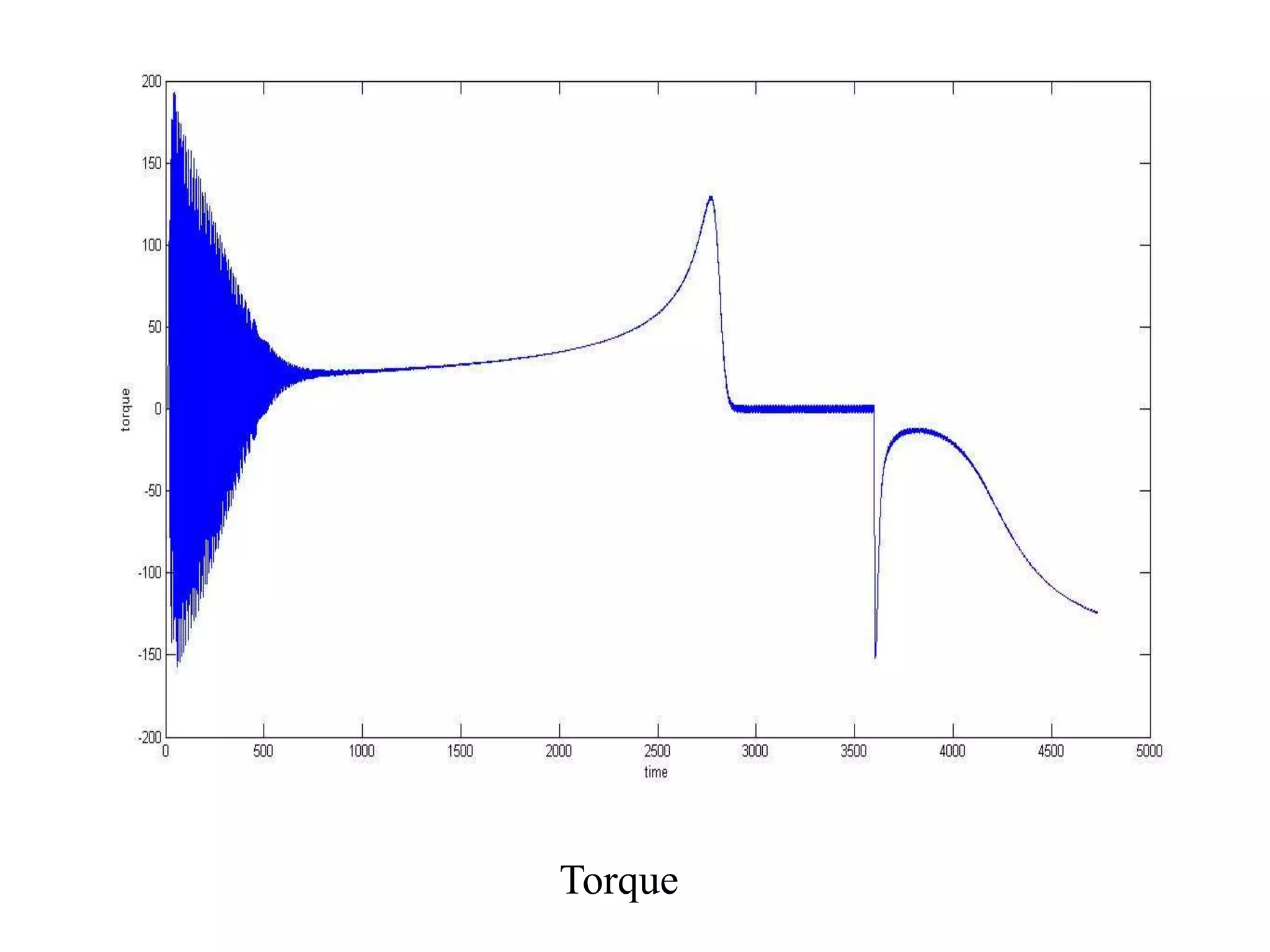
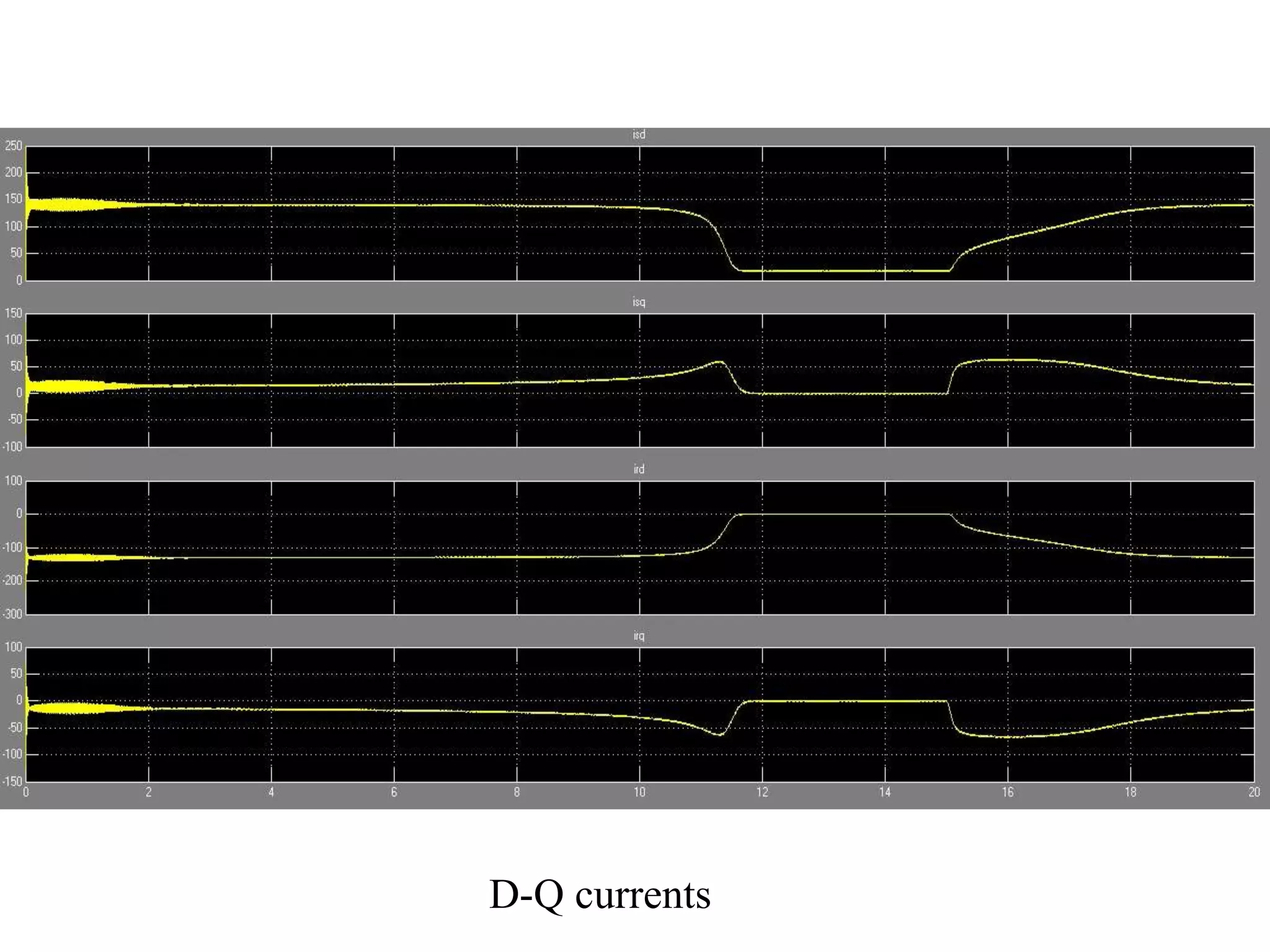
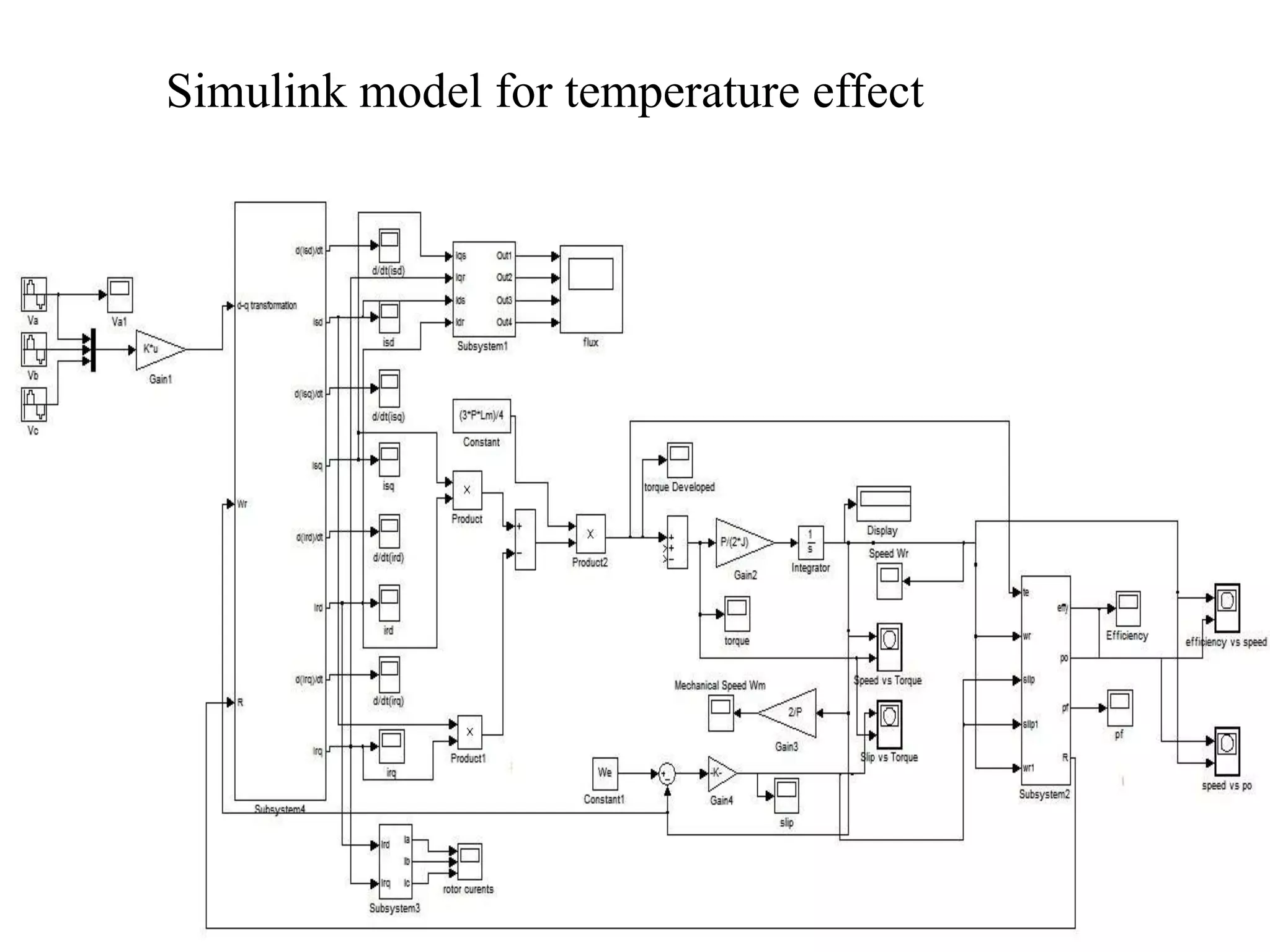
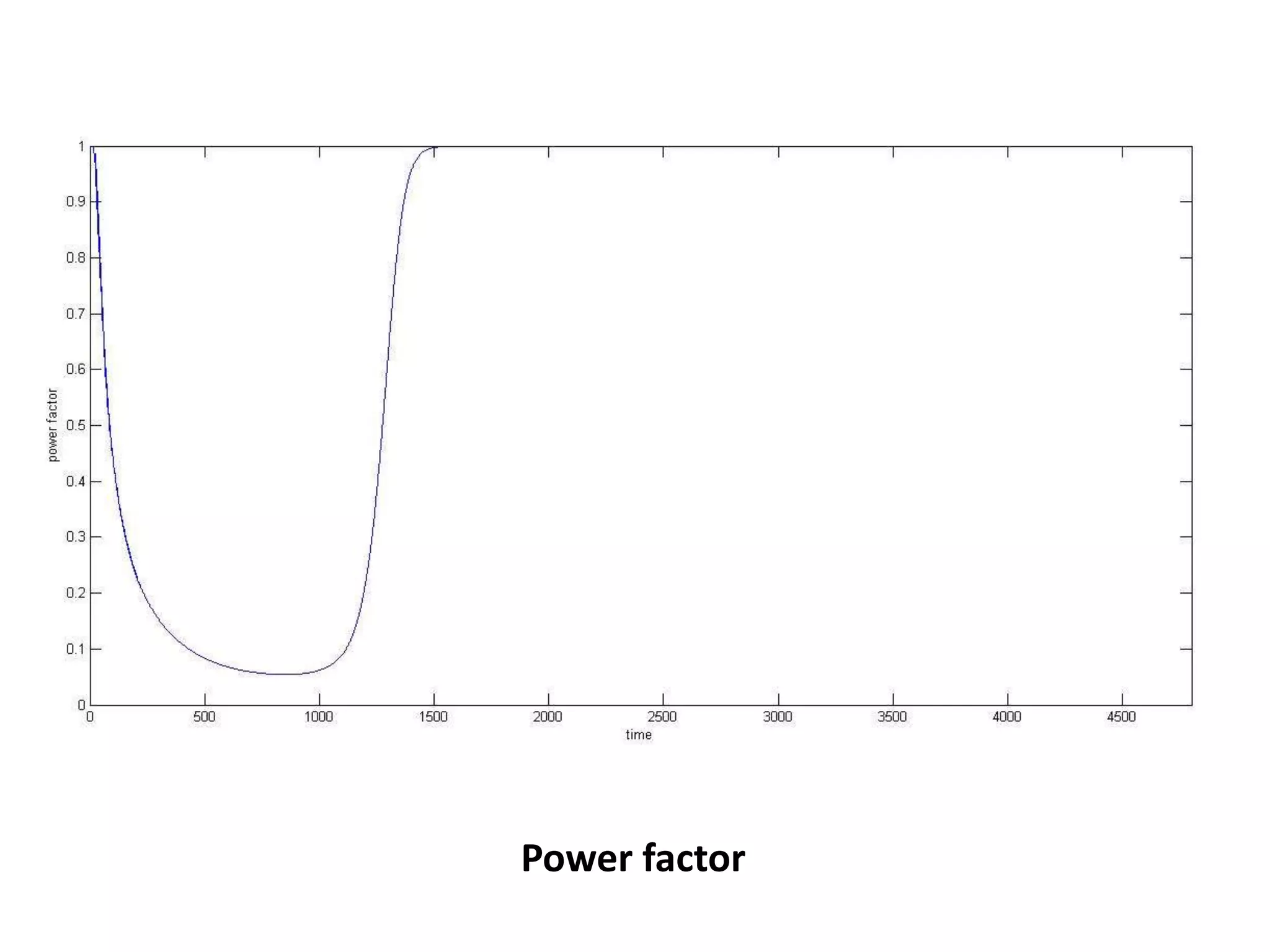
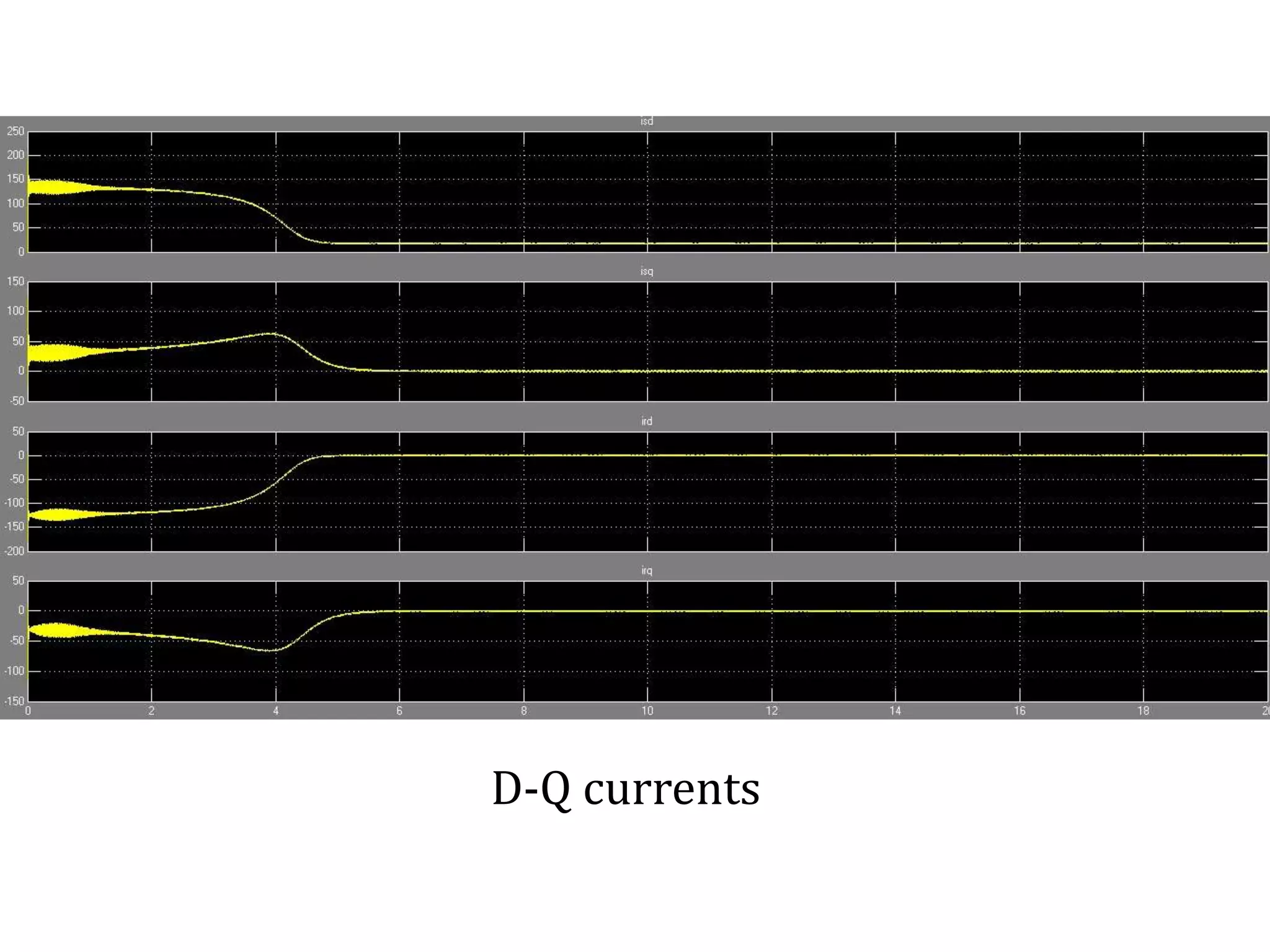
The document presents a project on induction motor modeling and applications, focusing on objectives, methodology, simulation results, and conclusions regarding the influence of temperature on motor parameters. Key findings include the development of equations for torque, rotor speed, and the impact of heating on efficiency and power factor, achieved through simulink modeling. Future work aims to enhance control algorithms for automatic speed adjustment and hardware implementation.

1. A Project on
Induction Motor Modeling And
Applications
By
Deepa Kokati
Sachin S
Shweta Joshi
Venkanagouda P. C
Department of Electrical and Electronics Engineering
K. L. E. Institute Of Technology, Hubli.
Under the guidance of
Prof.Gurunayk C. N.

2. CONTENTS
• Objectives
• Methodology
• Simulation Results
• Application
• Conclusion and future work
• Reference

3. OBJECTIVES
• AC motor control is to make the rotor turn at a desired
speed despite load variations by d-q modeling
observer

4. LITERATURE SURVEY
• The research so far discussed about different
modeling based on different reference frame
theories.
• Few discussed the application like control of
speed, Torque, Flux etc.
• However analysis of effect of temperature on
induction motor system is not carried out.

5. Park Transformation: The Park’s transformation is a
three-phase to two-phase transformation for machine
analysis.
5

bI
aI
cI
qi
di
cos Base componen
sin( ) Vertical Component
t
q a
d a
i I
i I





cos(120 ) Base component
sin( (120 )) Vertical Component
d b
q bi I
i I


  



120  240 
cos(240 ) Base componen
sin( (240 )) Vertical C
t
omponen
d
q c
c
i I
i I


 
 



qi
di

6.  
 1
2
2 4
cos cos cos
3 3
2 4
sin sin sin .
3 3
d a
q b
o c
o o o
i i
n
i i
n
i i
K K K
 
  
 
  
    
     
       
                              
 
 
To complete the transformation, it remains to assign
values to and1
2
n
n
oK
6
• Triphase system and its equivalent two-phase system .
• Both systems create the same MMF
• Thus the relation between three phase current and
equivalent two phase current is given by
   , dqo abcor i P i      

7.    
1
abc dqoi P i

      
 
1 1
1
2 2
2 3 3
0 .
3 2 2
1 1 1
2 2 2
P
 
  
 
 
  
 
 
 
 
•Following matrix is obtained by substituting,
• Thus park transformation preserves amplitude and
energy.
7
0 
•The inverse transformation,

8. Voltage equations
Flux equations
Where,
Synchronous Speed , or Speed of RMF
Rotor Speed
s
r




[ ] [ ]
[ ] [ ]
sdq s sdq sr rdq
rdq r rdq sr sdq
L i M i
L i M i


 
 
[ ]
[ ] [ ]
[ ]
[ ] [ ]
sabc
sabc s sabc
rabc
rabc r rabc
d
V R i
dt
d
V R i
dt


 
 
Basic Voltage Equations
( )
( )
sd
sd s sd s sq
sq
sq s sq s sd
rq
rd r rd s r rq
rq
rq r rq s r rd
d
V R i
dt
d
V R i
dt
d
V R i
dt
d
V R i
dt

 

 

  

  
  
  
   
   

9. 1
[ ]
[ ]
( )
[ ]
( )
sd sd rd s sd s
sr s sq sr rq
s s s s
sq sq s sq rqsr s
s sd sr rd
s s s s
rd rd sr sd s rr
rd r rq sr sq
r r r r
rq rq r rq sqsr s r
r r r
di V di R i
M L i M i
dt L L dt L L
di V R i diM
L i M i
dt L L L dt L
di V M diR
i L i M i
dt L L L dt L
di V R i diM
dt L L L dt L


 
 
    
    

    

    [ ]r rd sr sd
r
L i M i
Final equations

10. 3
( )
4
em m qs dr ds qrT PL i i i i 
2
r em
P
T dt
J
  
•Torque Equation
•Expression for Rotor Speed Developed
2 r
m
P

 
• Effect change in temperature in rotor is considered and
observed
• Similarly efficiency, power factor and slip are calculated
using basic equations and considering all possible losses.

11. • 20 hp,
• 460V, 50Hz, 3
• Induction motor with the following equivalent
circuit parameters:
Rs = 0.087 Ls = 0.0425 H
Rr= 0.187 Lr= 0.043H
Lm =0.04H
P = 4 We=500 rpm
Friction=10Nm/rad Stator copper loss=700w
Temperature coefficient=
Motor ratings
3
3.9 10 /o
C


12. Simulink model for normal operating

13. Speed

14. Speed v/s torque

15. Slip

16. Slip v/s torque

17. D-Q currents

18. Efficiency

19. Application
• Fault detection and analysis of effect of temperature variation on
Induction motor parameters.
Fault detection :
• a sudden load is applied for very short duration of time, when
Induction motor is at steady state. Then its effect on torque, speed,
current, slip, and flux are observed.

20. Simulink model for fault detection

21. Speed

22. Torque

23. D-Q currents

24. Simulink model for temperature effect

25. Power factor

26. D-Q currents

27. Fluxes of D-Q axis

28. Temperature variation
• the effect of change in temperature can be observed
immediately on, change in resistance of the windings. This
causes change in currents, fluxes, and power factor. Analysis is
carried out to investigate the effect of change in temperature on
Induction motor parameters

29. Conclusion And Future Work
• Implementation of Induction motor in simulink model.
• Any Induction machine control estimation algorithm can
be simulated in the simulink environment with this model,
without actually using sensors.
Future work
• Controller can be designed to obtain desired speed
automatically with change in loading conditions.
• Kalman estimator can be designed for accurate estimation
applications.
•Hardware implementation can be done.

30. REFERENCES
[1]Norman S Nise, “Control Systems Engineering”, Wiley Student Edition, 5th Edition, 2009
[2] Joseph J Distefano III and other, “Feedback and Control Systems”, Schaum’s Outlines,
TMH, 2ndEdition, 2007
[3] Ashfaq Hussain, “Electrical Machines”, Dhanpat Rai Publications
[4] Katsuhiko Ogata, “Modern Control Engineering”, PHI,5th Edition, 2010
[5] Fouad Giri “AC electric motors control”: advanced design techniques and applications ,
John Wiley & Sons, Ltd. 2013
[6] Chee-Mun ong , “Dynamic simulation of electric machinary”,using matlab/simulink
[7] Krstic M, Kanellakopoulos I, and Kokotovic P (1995) “Nonlinear and Adaptive Control
Design”. John Wiley & Sons. Leonard W (2001) “Control of Electrical Drives”. Springer,
New York.
[8] Novotnak RT, Chiasson J, and Bodson M (1999) High performance mtion control of an
induction motor with magnetic saturation, IEEE Transactions on Control Systems
Technology, 7, 315–327.
[9] Astolfi A, Karagiannis D, and Ortega R (2007) “Nonlinear and Adaptive Control with
Applications”. Springer. Besanc¸on G (2007) “Nonlinear Observers and Applications”.
Springer
[10] Khalil HK and Strangas EG (1996) Robust speed control of induction motors using
position and current measurement. IEEE Transactions on Automatic Control, 41, 1216–
1220.
[11] Dorf & Bishop- Pearson education, “Modern control systems”, 11th Edition 2008.