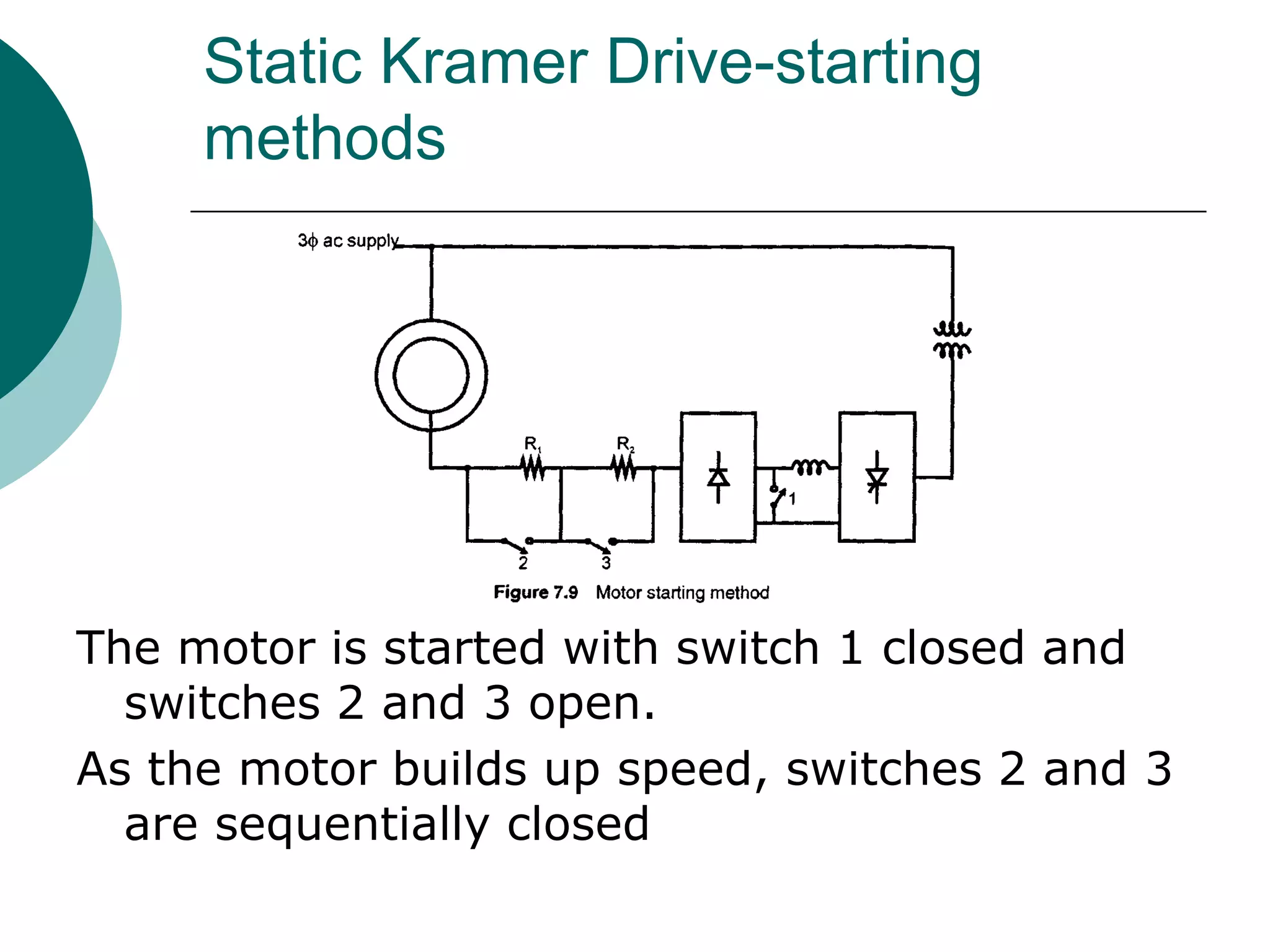
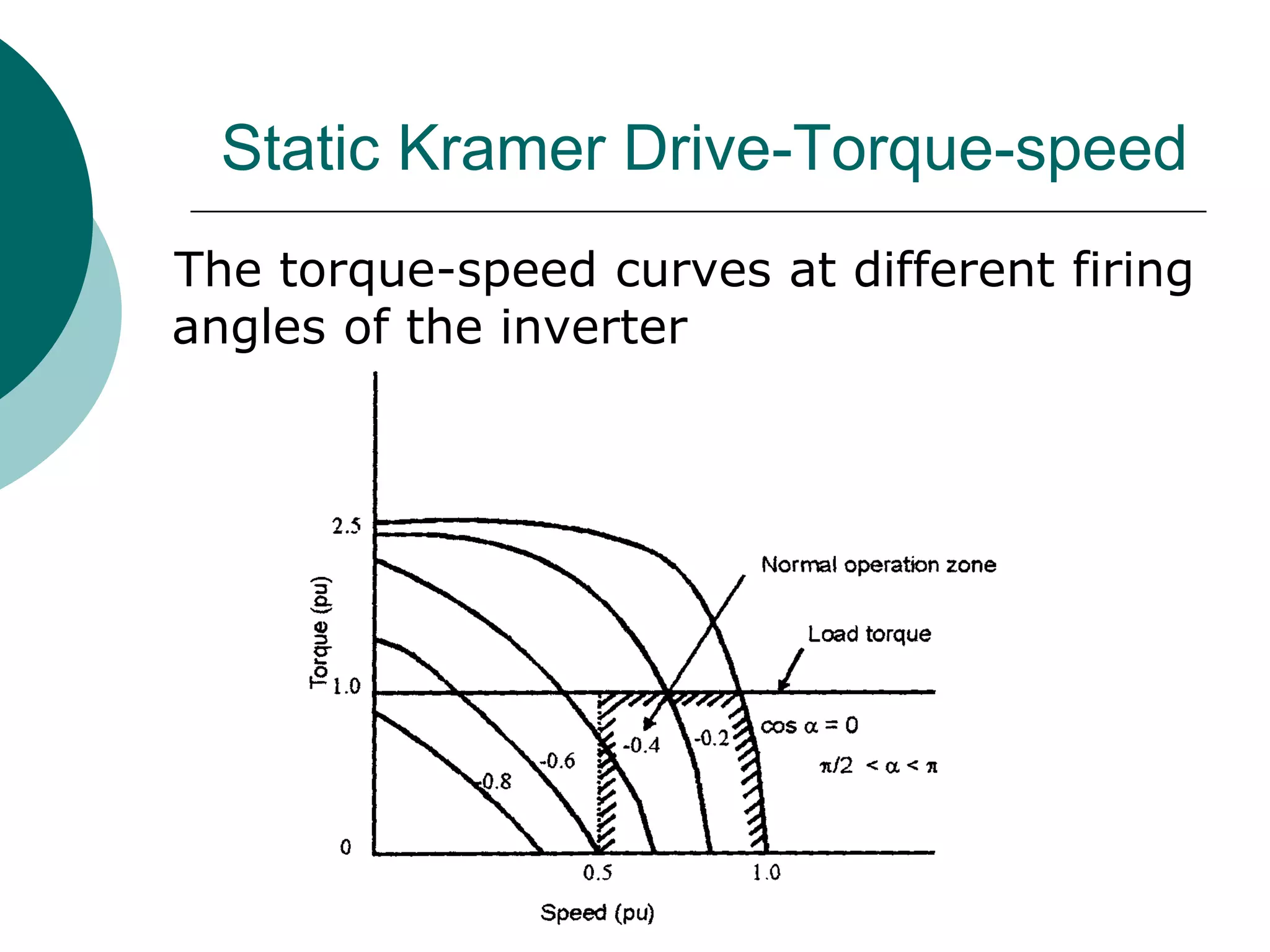
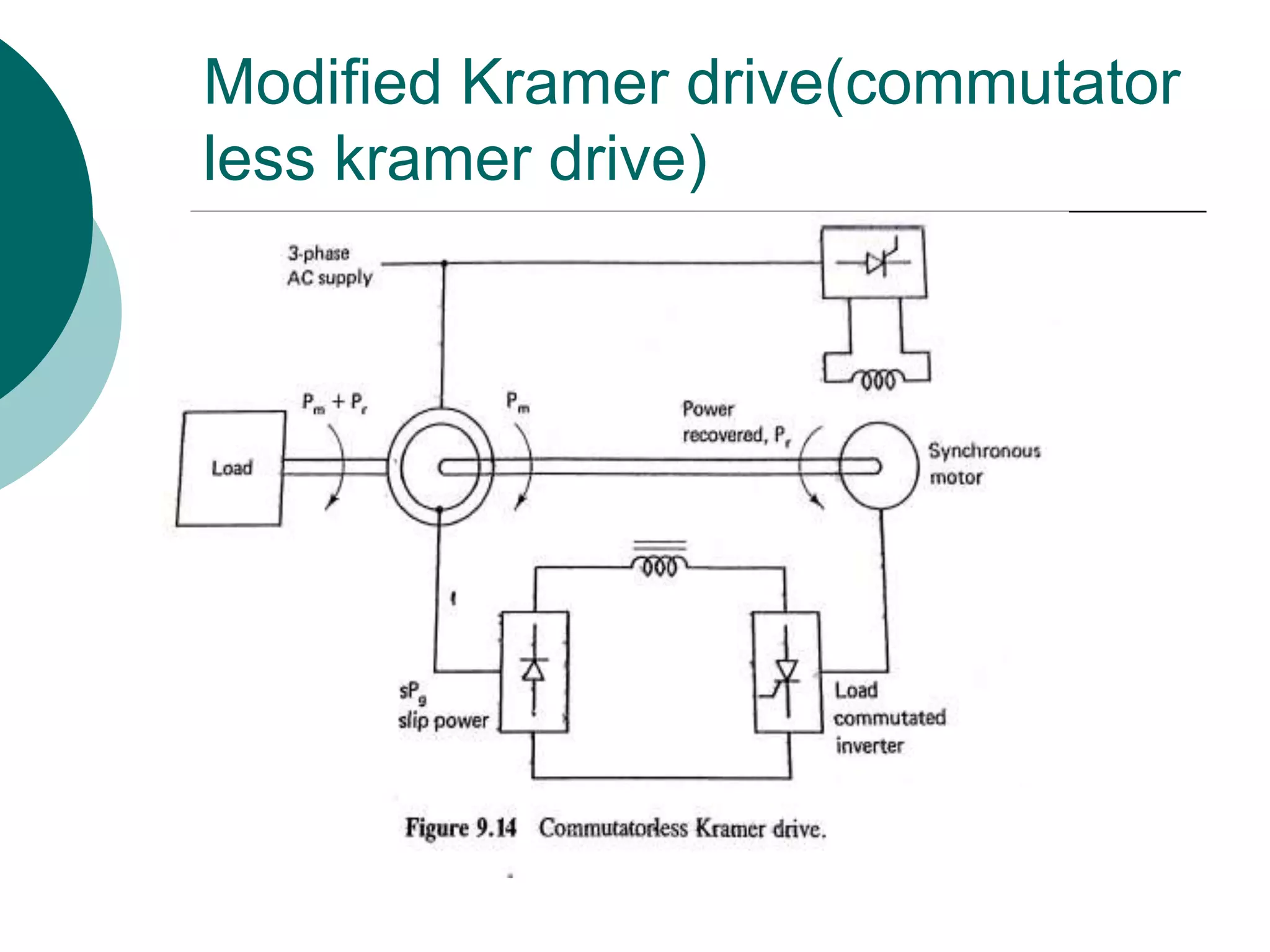
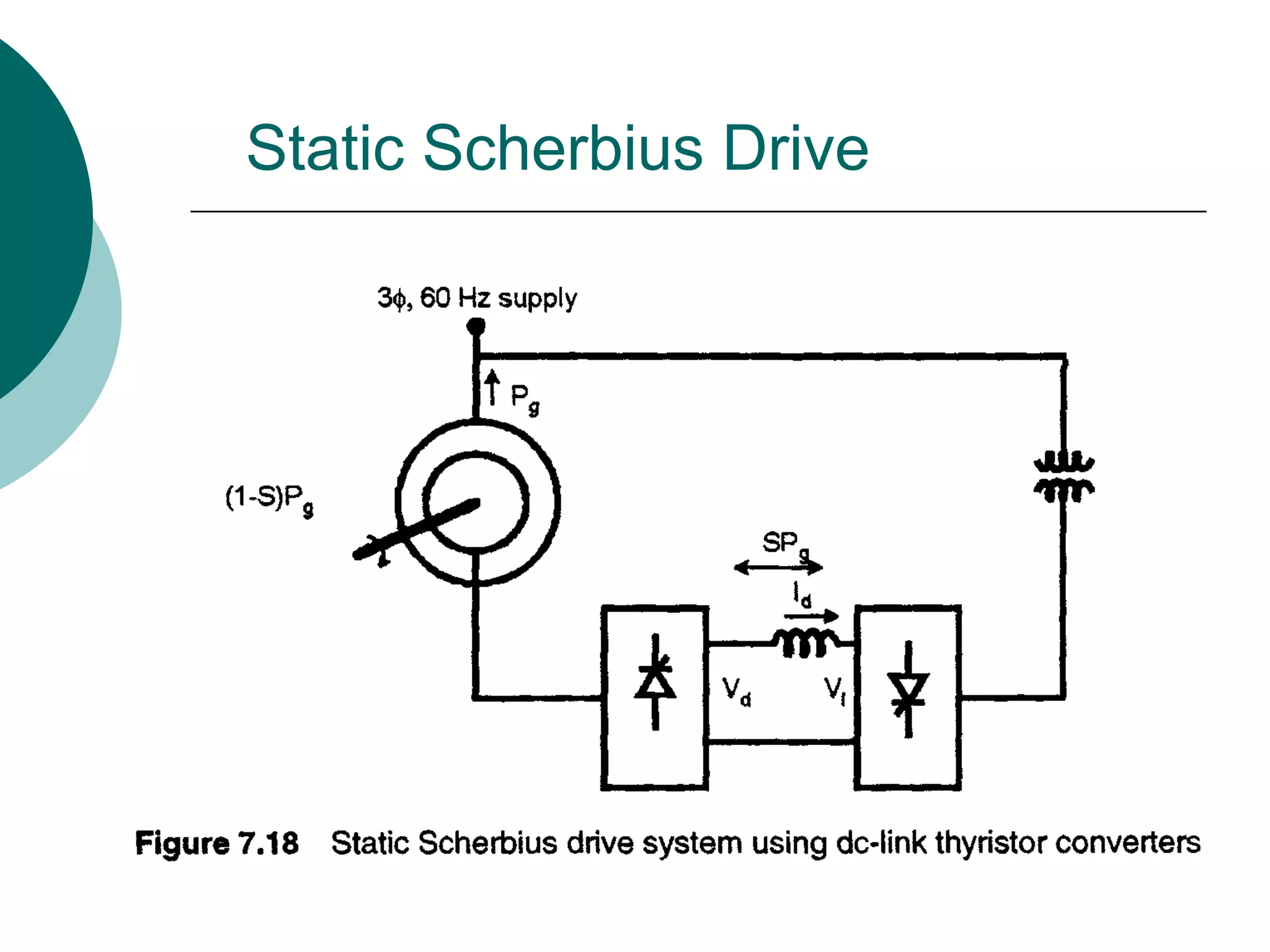
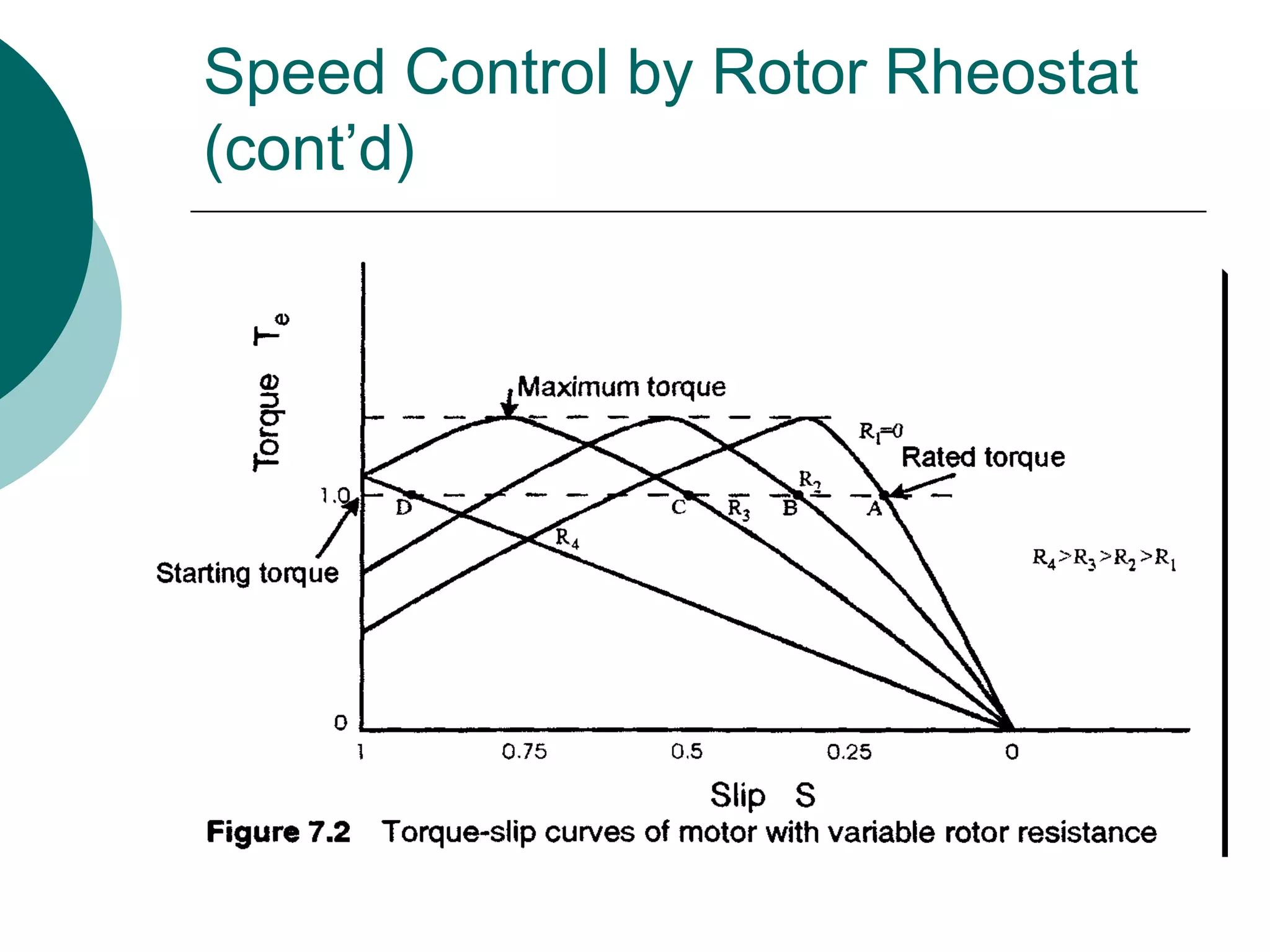
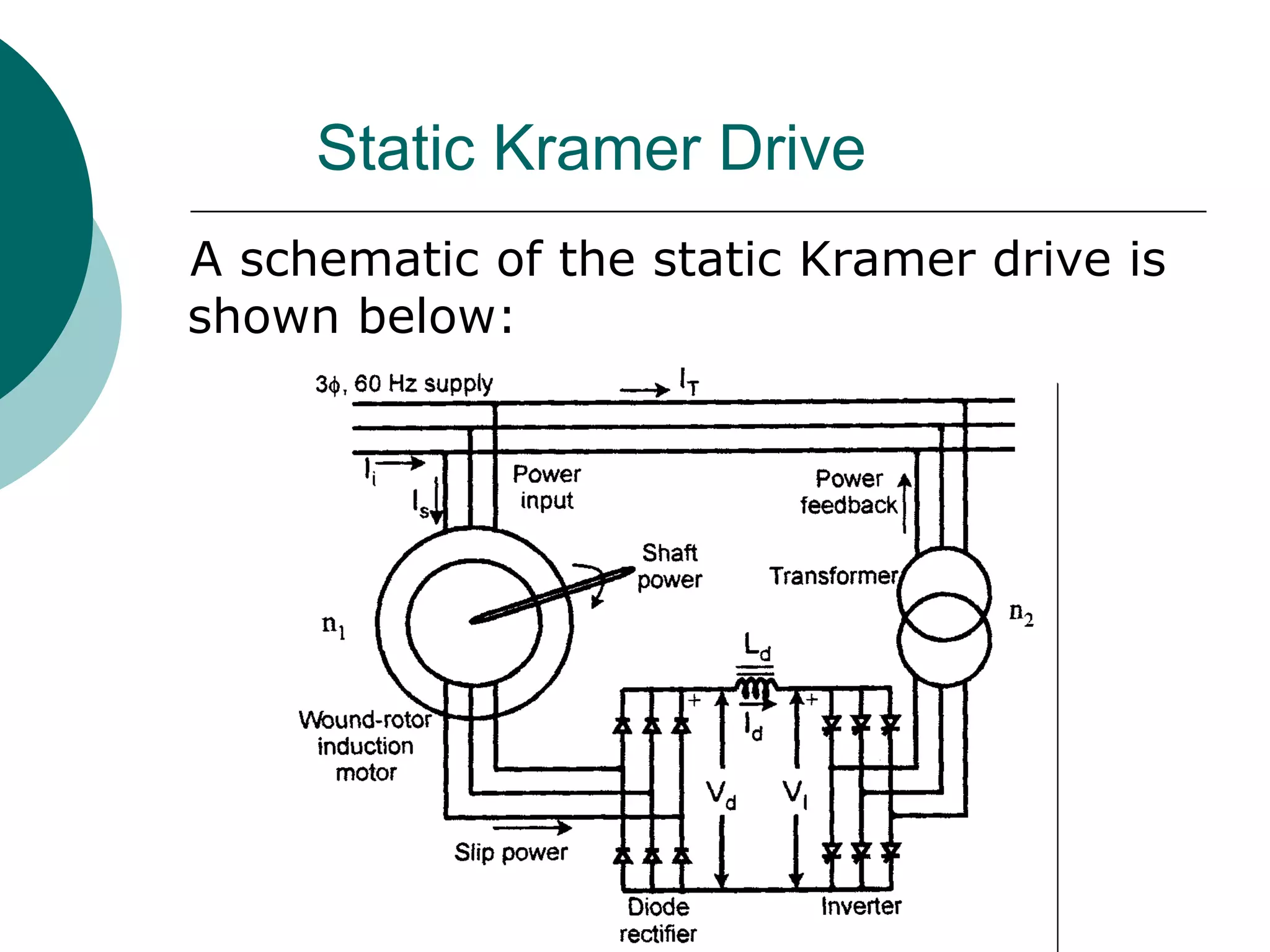
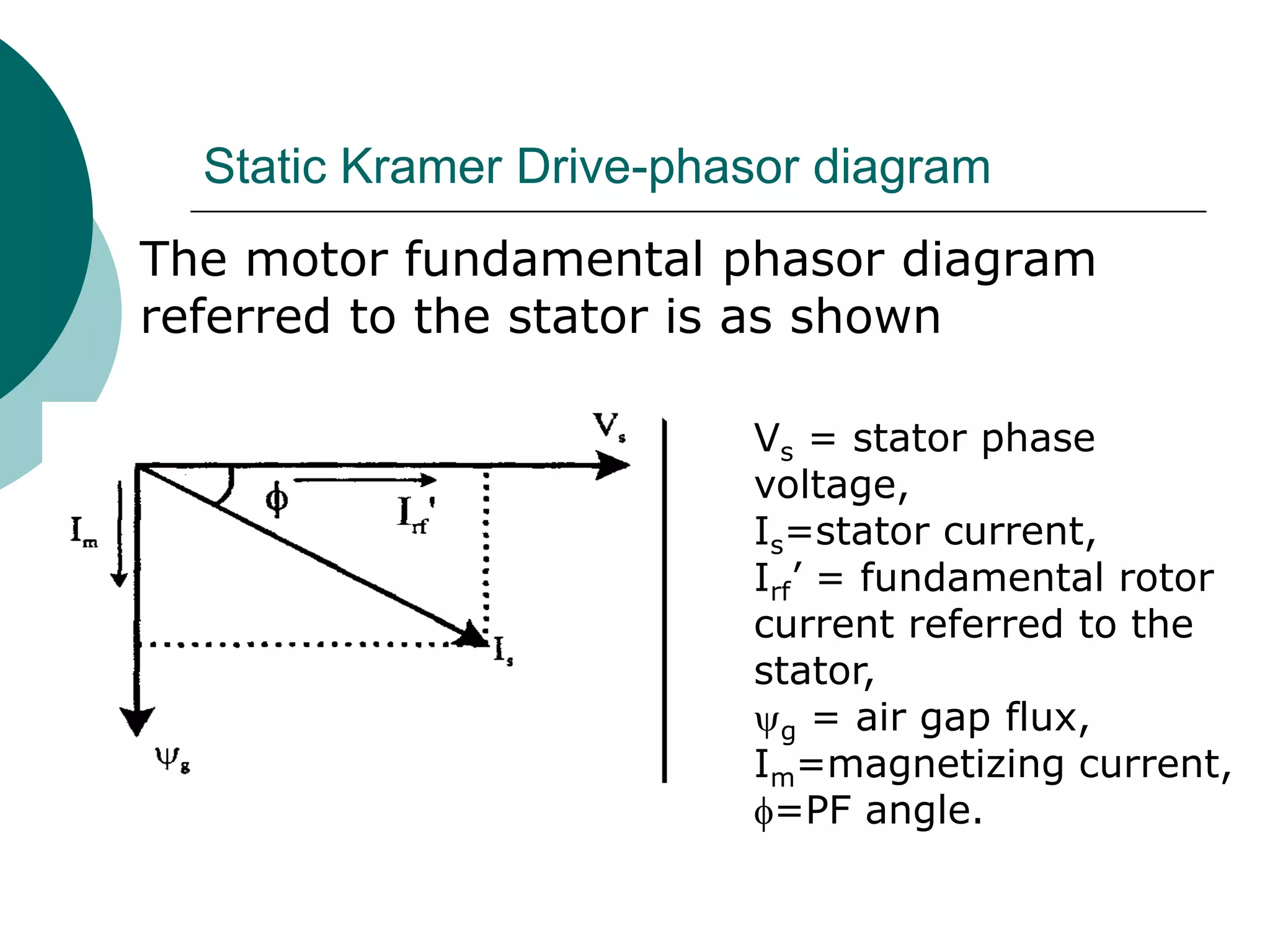
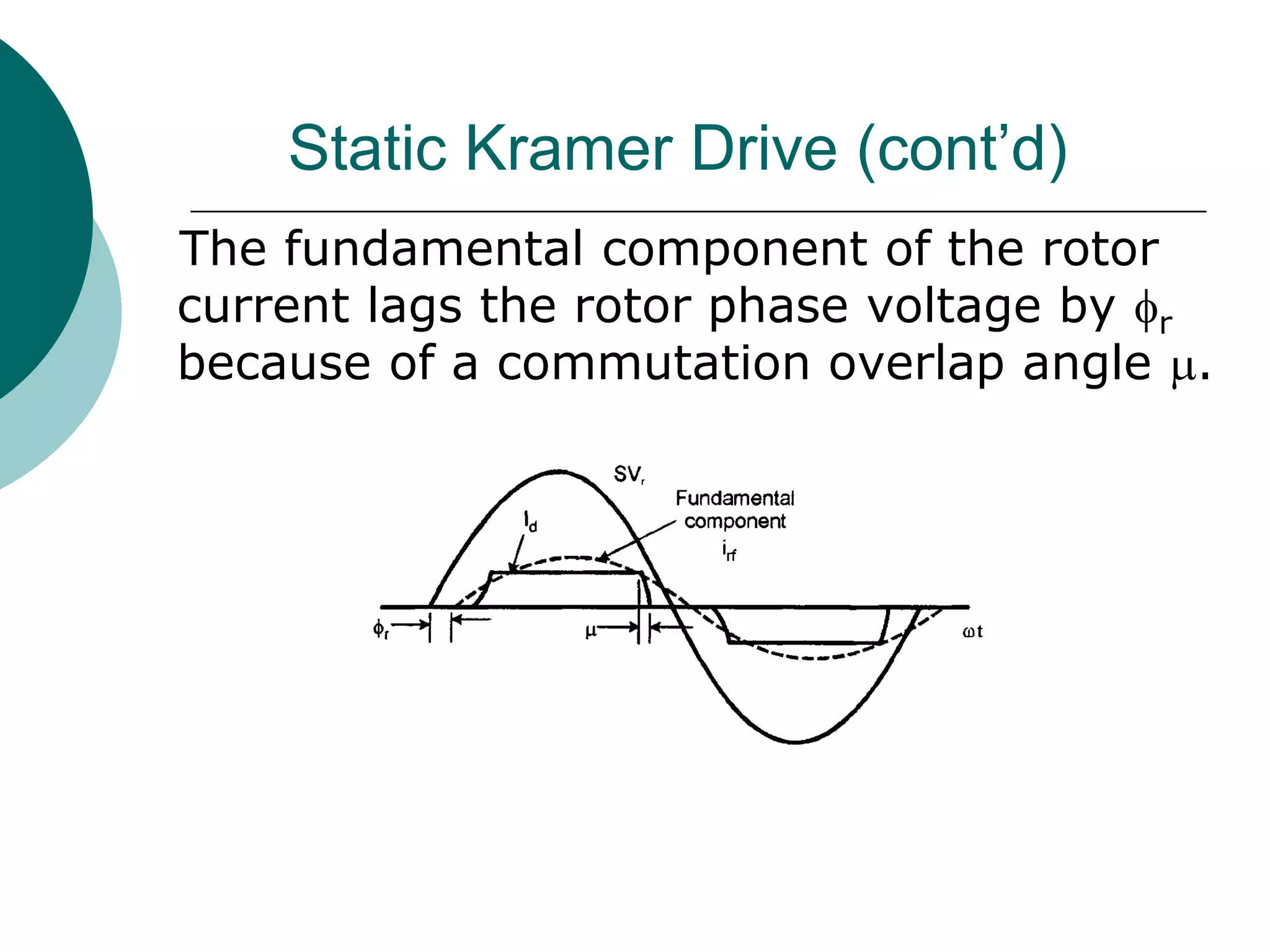
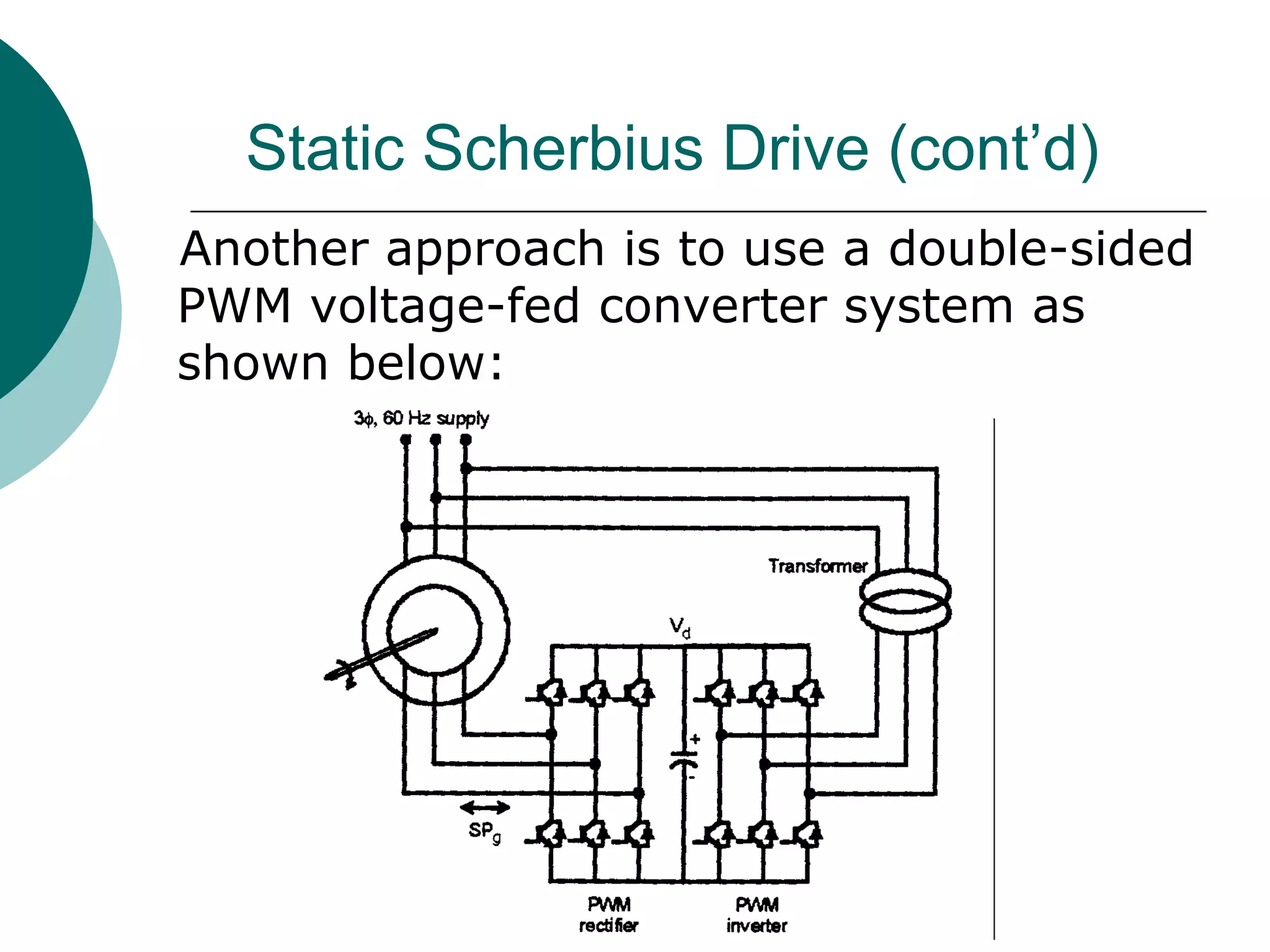
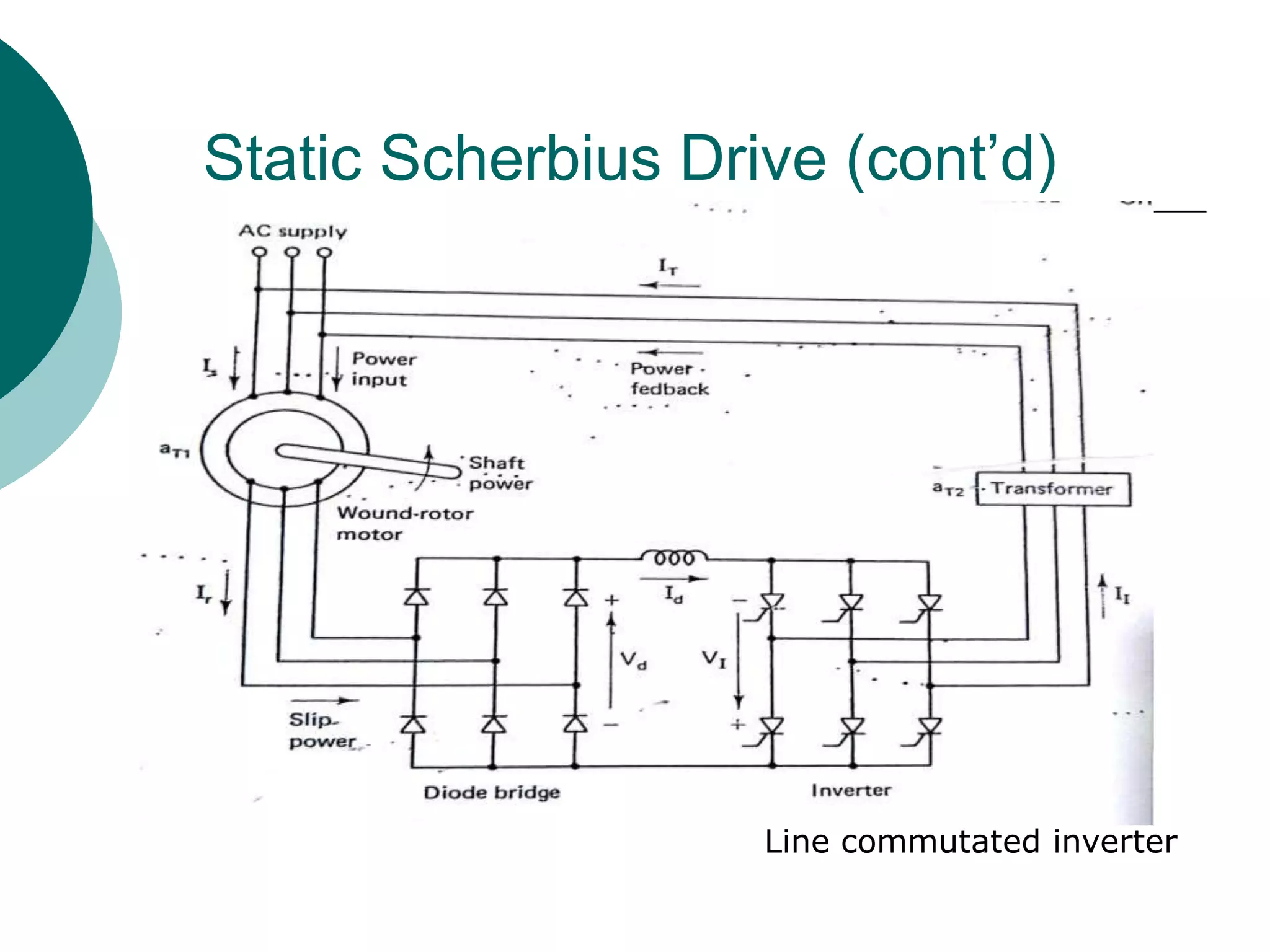
This document discusses various rotor control techniques for induction motors, including: 1) Static rotor resistance control, which is simple but inefficient as slip power is wasted in rotor resistance. 2) Slip power recovery schemes like static Kramer and Scherbius drives that convert slip power to AC line power to improve efficiency. 3) Injection of voltage in the rotor circuit using a Schrage motor to produce an EMF that is injected at slip frequency to control speed. 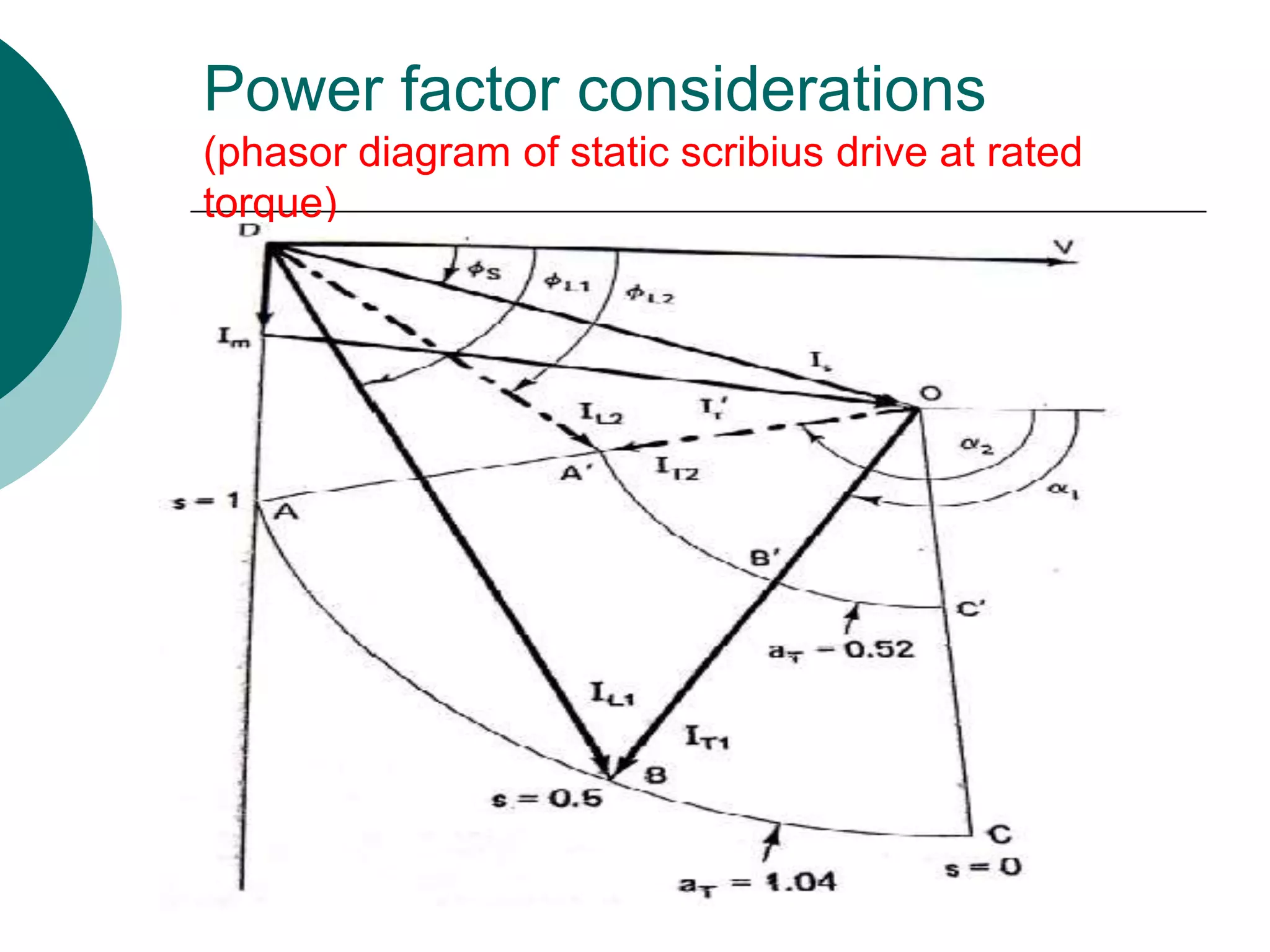The document provides details on operating principles, equivalent circuits, torque expressions, and power factor considerations for different rotor control induction motor drives.

1. UNIT III
ROTOR CONTROLLED INDUCTION MOTOR
DRIVES
SYLLABUS:
STATIC ROTOR RESISTANCE CONTROL
INJECTION OF VOLTAGE IN THE ROTOR CIRCUIT
STATIC SCHERIBIUS DRIVES
POWER FACTOR CONSIDERATIONS
MODIFIED KRAMMER DRIVE

2. Introduction
The portion of air gap power which is not
converted into mechanical power is called slip
power
Slip rings allow easy recovery of the slip
power
It can be electronically controlled to control
the speed of the motor.

3. Introduction
The oldest and simplest technique to invoke this
slip-power recovery induction motor speed control
is to mechanically vary the rotor resistance
Rotor resistance cotrol
.

4. Slip-power recovery drives - applications
 Large-capacity pumps and fan drives
 Variable-speed wind energy systems
 Shipboard VSCF (variable-speed/constant
frequency) systems
 Variable speed hydro-pumps/generators
 Utility system flywheel energy storage
systems

5. Speed Control by Rotor Rheostat
The torque-slip equation for an induction
motor is given by:
 
2
2 2 2
3 .
2 / ( )
sr
e
e s r e ls lr
VRP
T
s R R s L L 
 
  
    

6. Speed Control by Rotor Rheostat
(cont’d)

7. Speed Control by Rotor Rheostat
(cont’d)
1. Very simple,
2. Low cost
3. Good power factor
4. High torque to current ratio
5. Wide range of speed
6. Including starting and braking
7. It is also very inefficient because the slip
energy is wasted in the rotor resistance.

8. Static Rotor Rheostat control
It is also very inefficient because the slip
energy is wasted in the rotor resistance

9. Types of slip power recovery
schemes
Instead of wasting the slip power in the
rotor circuit resistance, a better approach
is to convert it to ac line power and return
it back to the line.
Static Kramer Drive - only allows
operation at sub-synchronous speed.
Static Scherbius Drive - allows operation
above and below synchronous speed.

10. Static Kramer Drive
A schematic of the static Kramer drive is
shown below:

11. Static Kramer Drive (cont’d)
The machine air gap flux is constant.
The rotor current is ideally a 6-step wave
in phase with the rotor voltage.

12. Static Kramer Drive-phasor diagram
The motor fundamental phasor diagram
referred to the stator is as shown
Vs = stator phase
voltage,
Is=stator current,
Irf’ = fundamental rotor
current referred to the
stator,
g = air gap flux,
Im=magnetizing current,
=PF angle.

13. Static Kramer Drive (cont’d)
Voltage Vd is given by:
where s=per unit slip,
VL= stator line voltage
n1=stator-to-rotor turns ratio.
The inverter dc voltage VI is given by:
where n2=transformer turns ratio
=inverter firing angle.
1
1.35 L
d
sV
V
n

2
1.35 cosL
I
V
V
n



14. Static Kramer Drive (cont’d)
the torque will be expressed as:
1
1.35
2
L
e d
e
VP
T I
n
 
  
 

15. Static Kramer Drive (cont’d)
The fundamental component of the rotor
current lags the rotor phase voltage by r
because of a commutation overlap angle .

16. Static Kramer Drive (cont’d)
At zero speed (s=1) the motor acts as a
transformer and all the real power is
transferred back to the line (neglecting
losses).
The motor and inverter only consume
reactive power.
At synchronous speed (s=0) the power factor
is the lowest .
Power factor increases as slip increases.

17. Static Kramer Drive-starting
methods
The motor is started with switch 1 closed and
switches 2 and 3 open.
As the motor builds up speed, switches 2 and 3
are sequentially closed

18. Static Kramer Drive-Torque-speed
The torque-speed curves at different firing
angles of the inverter

19. Harmonics in a Static Kramer Drive
The rectification of slip-power causes
harmonic currents in the rotor which are
reflected back into the stator.
This results in increased machine losses.

20. Power Factor Improvement
The static Kramer drive is characterized
by poor line PF because of phase
controlled inverter.
One scheme to improve PF is the
commutator-less Kramer drive

21. Modified Kramer drive(commutator
less kramer drive)

22. Modified Kramer drive(commutator
less kramer drive)
The slip power taken from the rotor
for speed control by converting it to
mechanical power in an auxiliary
motor mounted on the induction
motor shaft
The mechanical power produced by
the auxiliary motor supplements the
main motor power

23. Modified Kramer drive(commutator
less kramer drive)
 Better power factor
 Lower harmonic content
 Electric power not feed back to the
line
 Problems associated with the feed
back of power are also eliminated.

24. Static Scherbius Drive

25. Static Scherbius Drive (cont’d)
Another approach is to use a double-sided
PWM voltage-fed converter system as
shown below:

26. Static Scherbius Drive (cont’d)
Line commutated inverter

27. Static Scherbius Drive (cont’d)
Voltage Vd is given by:
where s=per unit slip,
VL= stator line voltage
n1=stator-to-rotor turns ratio.
The inverter Output ac voltage VI is
given by
where n2=transformer turns ratio
=inverter firing angle.
1
1.35 L
d
sV
V
n

2
1.35 cosL
I
V
V
n



28. Static Scherbius Drive (cont’d)

29. Static Scherbius Drive (cont’d)
1
1.35
2
L
e d
e
VP
T I
n
 
  
 
Torque is approximately proportional to
dc link current since fundamental rotor
current is proportional to dc link current

30. Power factor considerations
(phasor diagram of static scribius drive at rated
torque)

31. Power factor considerations
All the phasors are reffered to the stator or line side
 Vs = stator phase voltage,
 Is=stator current,
 Ir’ = fundamental rotor current
referred to the stator,
 g = air gap flux,
 Im=magnetizing current,
 COS  s= Motor PF
 COS  L1 = Fundamental drive PF

32. Power factor considerations
(conclusions from the phasor diagram)
 The drive power factor is maximized when
“aT’’ is chosen to obtain the drive operation
at the maximum permissible firing angle at
the lowest speed
 The narrower speed range
 The greater the power factor

33. INJECTION OF VOLTAGE IN THE ROTOR CIRCUIT
 The speed control of three-phase slip-
ring induction motor can be done using
injected EMF in the rotor circuit.
 In the Schrage motor slip frequency
EMF is produced and injected into
secondary winding on the stator by
means of brushes.

34. INJECTION OF VOLTAGE IN THE ROTOR CIRCUIT
Equivalent circuit of induction motor with injected
EMF in rotor circuit

35. INJECTION OF VOLTAGE IN THE ROTOR CIRCUIT
Under steady state condition,
• Injected EMF referred to stator.
•The rotor quantities are referred to stator side.

36. INJECTION OF VOLTAGE IN THE ROTOR
CIRCUIT
The rotor voltage referred to stator is

37. INJECTION OF VOLTAGE IN THE ROTOR CIRCUIT
The expression for torque is given as

38. INJECTION OF VOLTAGE IN THE ROTOR CIRCUIT
The injected EMF is having slip frequency,
It may have phase difference with the rotor
voltage.
The machine can be made to run in sub- and
super-synchronous speed apart from normal
induction motor operation.