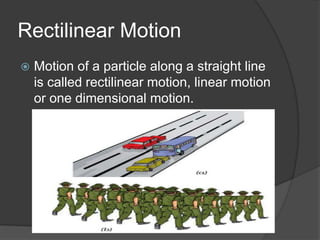
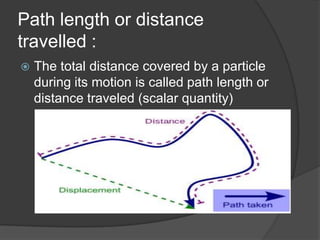
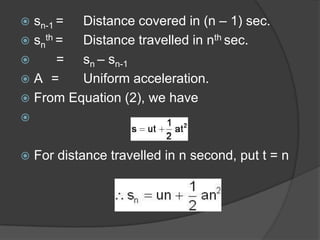
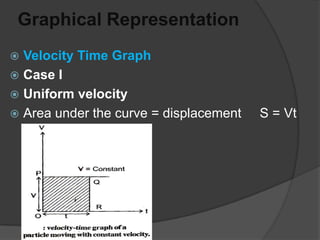
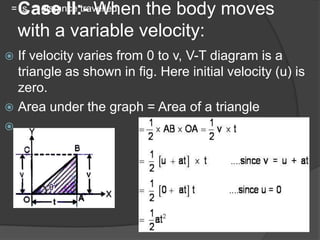
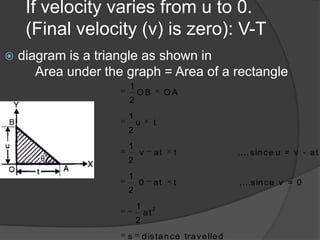
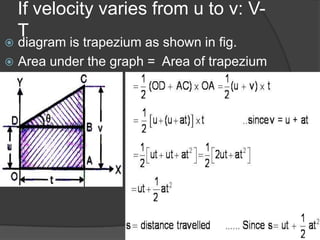
This document discusses key terms and equations related to rectilinear motion. Rectilinear motion refers to motion along a straight line. Kinematics deals with the motion of bodies without considering forces. Important concepts discussed include displacement, average and instantaneous velocity, acceleration, distance traveled, and equations of motion. Graphical representations of motion using velocity-time graphs are also presented for different scenarios including uniform velocity, variable velocity from rest to a final velocity, and variable velocity between two points.

1. Rectilinear Motion

2. Important Terms And
Definitions
1. Kinematics :
 It is the branch of dynamics which deals
with the forces acting on bodies in
motion without considering the mass of
a body and the forces which is
responsible to cause the motion.


3. Rectilinear Motion

Motion of a particle along a straight line
is called rectilinear motion, linear motion
or one dimensional motion.

4. 3.

To describe linear motion of a particle its
position at all times is to be specified.
The equations used in this case are
called ‘Equations of Motion’ or
‘Kinematical equations’.

5. 4. Every motion is related to
the observer:

Position of a particle in motion is
described in terms of distance from
reference point or origin.

6. Path length or distance
travelled :

The total distance covered by a particle
during its motion is called path length or
distance traveled (scalar quantity)

7. Displacement :

Change in position of a moving particle
in a particular direction is called
displacement. Displacement is the
shortest distance between two positions
of a moving particle in a particular
direction (vector quantity)

8. 
Displacement and distance traveled are
equal in rectilinear motion but distance
traveled is greater than displacement in
any other motion.

9. Average velocity (vector
quantity)

The average velocity of a moving
particle is defined as the displacement
divided by the interval in which it has
occurred

avg vel V
x
t

10. 
Average speed : Average speed of a moving
particle is defined as total distance travelled
divided by time taken

Avg speed V = total distance traveled / time

11. 
Acceleration : Acceleration of a moving
body is defined as the rate of change of
velocity with respect to time.

12. Equation of motion, when Distance (s)
Travelled by a Body Moving with a
Uniform Velocity:
We know that,
 Distance travelled = Average velocity x time

S
u
v
t
2
 we have, v = u + at, substitute this in equation
(1), we get

14. Equation of Motion, when Velocity of a
Body Moving with Uniform Acceleration
after Covering a Distance ‘S’

15. Equation of Motion, when a Distance
Travelled in nth Second by a particle
(or Body) Moving with Uniform
Acceleration:
Consider a body in rectilinear motion
moving with initial velocity (u) and
uniform acceleration (a). In nth second, it
acquires a velocity (v) and covers a
distance (s).
u =
Initial velocity of a body:
v =
Final velocity of a body
n =
Number of second:
 sn =
Distance travelled in n sec.


16. Distance covered in (n – 1) sec.
Distance travelled in nth sec.

= sn – sn-1
A =
Uniform acceleration.
 From Equation (2), we have
 sn-1 =
 snth =


For distance travelled in n second, put t = n

17. For distance travelled in (n – 1) second, put t = n – 1

19. Graphical Representation
Velocity Time Graph
 Case I
 Uniform velocity
 Area under the curve = displacement

S = Vt

20. Case II:- When the body moves
with a variable velocity:
= s = distance travelled.
If velocity varies from 0 to v, V-T diagram is a
triangle as shown in fig. Here initial velocity (u) is
zero.
 Area under the graph = Area of a triangle



21. 
s = distance travelled.

22. If velocity varies from u to 0.
(Final velocity (v) is zero): V-T

diagram is a triangle as shown in
Area under the graph = Area of a rectangle
1
2
1
2
1
2
1
2
OB
u
t
v
at
t
.... s in c e u = v - a t
0
at
t
....s in c e v = 0
1
2
s
OA
at
2
d is ta n c e tra v e lle d

23. 
Negative sign indicates that there is
retardation.
S lo p e
u
t
ta n
a
u
t
.....sin ce -a = re ta rd a tio n .

24. If velocity varies from u to v: VT
diagram is trapezium as shown in fig.
 Area under the graph = Area of trapezium
