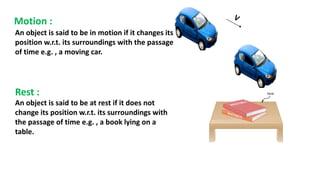
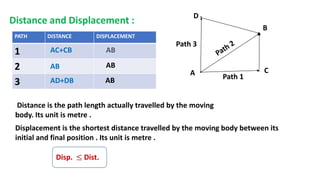
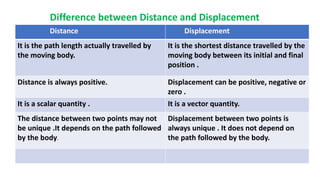
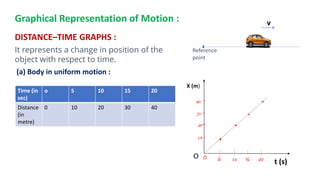
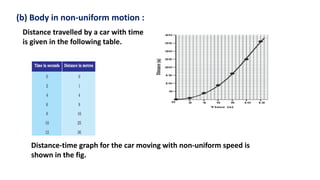
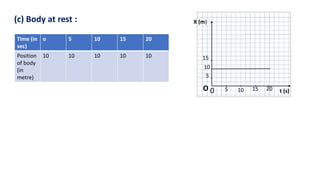
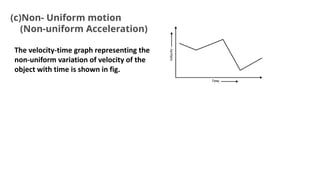
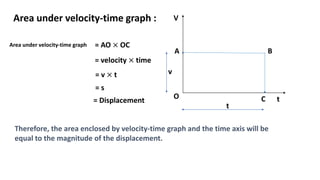
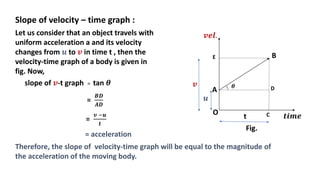
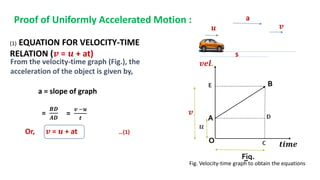
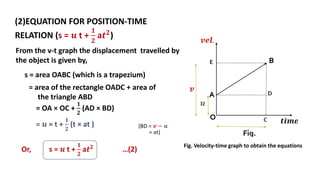
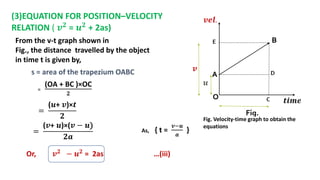
This document discusses motion in a straight line, including definitions of key terms like distance, displacement, speed, velocity, uniform motion, non-uniform motion, acceleration, and equations of motion. It defines distance as the total path length traveled, displacement as the shortest distance between initial and final positions, and distinguishes between scalar and vector quantities. Graphs of distance-time and velocity-time are presented for different motion types. Equations relating velocity, displacement, time, initial velocity, acceleration, and final velocity are derived for uniformly accelerated motion.

1. CH-3
Motion In Straight Line

2. Motion :
Rest :
An object is said to be at rest if it does not
change its position w.r.t. its surroundings with
the passage of time e.g. , a book lying on a
table.
An object is said to be in motion if it changes its
position w.r.t. its surroundings with the passage
of time e.g. , a moving car.

3. Rest and Motion are relative terms :
An object may appear to be moving for one
person and stationary for some other. A
person standing on the road–side perceives
the passengers as moving. However, a
passenger inside the bus sees his fellow
passengers to be at rest.
It indicates that Rest and Motion are relative
terms and not absolute terms.
What do these observations indicate?

4. Distance and Displacement :
A
B
C
D
Path 1
Path 3
PATH DISTANCE DISPLACEMENT
1
2
3
AC+CB
AB
AD+DB
AB
AB
AB
Distance is the path length actually travelled by the moving
body. Its unit is metre .
Displacement is the shortest distance travelled by the moving body between its
initial and final position . Its unit is metre .
Disp. ≤ Dist.

5. QUESTIONS:
1. An object has moved through a distance. Can it have zero displacement? If yes,
support your answer with an example.
Ans.
2. A farmer moves along the boundary of a square field of side 10 m in 40 s. What
will be the magnitude of displacement of the farmer at the end of 2 minutes 20
seconds?
Ans.

6. 3. Which of the following is true for displacement?
(a) It cannot be zero.
(b) Its magnitude is greater than the distance travelled by the object.

7. Question. The object starts its journey from O which is treated as its reference point
(Fig.). Let A, B and C represent the position of the object at different instants.
(a)At first, the object starts from O moves through C and B and reaches A. Find the
distance and displacement travelled by the object.
(b) Second time, the object starts from O moves through C and B and reaches A. Then it
moves back along the same path and reaches C through B. Find the distance and
displacement travelled by the object.
Sol.

8. Scalar Quantities and Vector Quantities :
A vector quantity is a quantity to represent which magnitude as well as
direction is necessary. Examples: displacement , velocity etc.
Scalar Quantities or scalars :
A scalar quantity is a quantity to represent which only magnitude
is necessary. Examples: Distance ,speed etc.
Vector Quantities or vectors :

9. Difference between Distance and Displacement
Distance Displacement
It is the path length actually travelled by
the moving body.
It is the shortest distance travelled by the
moving body between its initial and final
position .
Distance is always positive. Displacement can be positive, negative or
zero .
It is a scalar quantity . It is a vector quantity.
The distance between two points may not
be unique .It depends on the path followed
by the body.
Displacement between two points is
always unique . It does not depend on
the path followed by the body.

10. Speed of an object is defined as
the distance travelled by the
object per unit time.
Speed :
Speed =
𝑫𝒊𝒔𝒕𝒂𝒏𝒄𝒆
𝑻𝒊𝒎𝒆
v =
𝒔
𝒕
If an object travels a distance s in time t
then its speed v is,
Velocity
Velocity of an object is defined
as the displacement travelled
by the object per unit time.
Velocity =
𝑫𝒊𝒔𝒑𝒍𝒂𝒄𝒆𝒎𝒆𝒏𝒕
𝑻𝒊𝒎𝒆
If an object travels a displacement s in
time t then its velocity v is,
v =
𝒔
𝒕
It is a scalar quantity . Its SI unit is
metre/second written symbolically as
m/s or m𝒔−𝟏
.
It is a vector quantity . Its SI unit is
metre/second written symbolically as
m/s or m𝒔−𝟏
.

11. Uniform Motion – In case of uniform motion the velocity of an object
remains constant with change in time.
Non-uniform Motion – In case of non-uniform motion the velocity of an
object changes with time.
Average Speed :
If the motion of the object is non-uniform then we calculate the average
speed to signify the rate of motion of that object.
Average Speed =
𝑇𝑜𝑡𝑎𝑙 𝐷𝑖𝑠𝑡𝑎𝑛𝑐𝑒 𝑇𝑟𝑎𝑣𝑒𝑙𝑙𝑒𝑑
𝑇𝑜𝑡𝑎𝑙 𝑇𝑖𝑚𝑒 𝑡𝑎𝑘𝑒𝑛
Average Velocity :
If the motion of the object is non-uniform then the average
velocity is given as ,
Average Velocity =
𝑇𝑜𝑡𝑎𝑙 𝐷𝑖𝑠𝑝𝑙𝑎𝑐𝑒𝑚𝑒𝑛𝑡 𝑇𝑟𝑎𝑣𝑒𝑙𝑙𝑒𝑑
𝑇𝑜𝑡𝑎𝑙 𝑇𝑖𝑚𝑒 𝑡𝑎𝑘𝑒𝑛

12. Question. The object starts its journey from O which is treated as its reference point
(Fig.). Let A, B and C represent the position of the object at different instants.
(a)At first, the object starts from O moves through C and B and reaches A in 2 hr. Find
the average speed and average velocity of the object.
(b) Second time, the object starts from O moves through C and B and reaches A. Then it
moves back along the same path and reaches C through B in total time 3 hr. Find the
average speed and average velocity of the object.
Sol.

13. Question. An athlete completes one round of a circular track of
diameter 140 m in 40 s with uniform speed.
What will be the (a)distance covered,
(b) The displacement
(c) Average speed ,and
(d) Average velocity
at the end of 20 s?

14. Example: Usha swims in a 90 m long pool. She covers 180 m in one minute by
swimming from one end to the other and back along the same straight path. Find
the average speed and average velocity of Usha.
Sol.

15. Instantaneous speed and instantaneous velocity:
The magnitude of speed at a particular instance of time is called
Instantaneous Speed.
The velocity at a particular instance of time is called Instantaneous
Velocity.

16. Acceleration :
Acceleration is a measure of the change in the
velocity of an object per unit time.
acceleration =
𝑪𝒉𝒂𝒏𝒈𝒆 𝒊𝒏 𝒗𝒆𝒍𝒐𝒄𝒊𝒕𝒚
𝒕𝒊𝒎𝒆 𝒕𝒂𝒌𝒆𝒏
If the velocity of an object changes from an initial
value u to the final value v in time t, the acceleration
a is,
a =
𝒗 −𝒖
𝒕
In non-uniform motion, velocity varies with time. This kind of motion is known as
accelerated motion. A physical quantity is introduced here which is known as
acceleration.
It is a vector quantity . Its SI unit is m/𝒔𝟐 or m𝒔−𝟐

17. Example: Starting from a stationary position, Rahul paddles his bicycle to attain a
velocity of 6 m𝒔−𝟏 in 30 s. Then he applies brakes such that the velocity of the bicycle
comes down to 4 m𝒔−𝟏 in the next 5 s. Calculate the acceleration of the bicycle in both
the cases.

18. Graphical Representation of Motion :
DISTANCE–TIME GRAPHS :
It represents a change in position of the
object with respect to time.
(a) Body in uniform motion :
Time (in
sec)
o 5 10 15 20
Distance
(in
metre)
0 10 20 30 40
Reference
point
v
O
t (s)
X (m)

19. (b) Body in non-uniform motion :
Distance-time graph for the car moving with non-uniform speed is
shown in the fig.
Distance travelled by a car with time
is given in the following table.

20. (c) Body at rest :
Time (in
sec)
o 5 10 15 20
Position
of body
(in
metre)
10 10 10 10 10
t (s)
X (m)
O 0 5 10 15 20
5
10
15

21. VELOCITY-TIME GRAPHS :
(a)Constant
velocity (Uniform motion)
(b)Non- Uniform motion
(Uniform Acceleration)

22. (c)Non- Uniform motion
(Non-uniform Acceleration)
The velocity-time graph representing the
non-uniform variation of velocity of the
object with time is shown in fig.

23. Area under velocity-time graph :
O t
V
A B
C
Area under velocity-time graph = AO × OC
= velocity × time
= Displacement
Therefore, the area enclosed by velocity-time graph and the time axis will be
equal to the magnitude of the displacement.
v
t
= v × t
= s

24. Slope of velocity – time graph :
O
𝒗𝒆𝒍.
𝒕𝒊𝒎𝒆
Fig.
Let us consider that an object travels with
uniform acceleration a and its velocity
changes from 𝒖 to 𝒗 in time t , then the
velocity-time graph of a body is given in
fig. Now,
slope of 𝒗-t graph = tan 𝜽
𝒖
𝒗
t
A
B
E
C
D
𝜽
=
𝑩𝑫
𝑨𝑫
=
𝒗 −𝒖
𝒕
= acceleration
Therefore, the slope of velocity-time graph will be equal to the magnitude of
the acceleration of the moving body.

25. Equations of Uniformly Accelerated Motion :
Let us consider that an object travels with uniform acceleration a and its velocity
changes from 𝒖 to 𝒗 in time t after covering a distance s. The relations between
𝒖,𝒗, 𝒔, 𝒕 𝒂𝒏𝒅 a are known as equations of uniformly accelerated motion. There are
three such equations. As,
𝒗 = 𝒖 + at …(1)
s = 𝒖 t +
𝟏
𝟐
a𝒕𝟐 …(2)
𝒗𝟐 = 𝒖𝟐 + 2as …(3)
𝒖 𝒗
s
a

26. (1) EQUATION FOR VELOCITY-TIME
RELATION (𝒗 = 𝒖 + at)
Proof of Uniformly Accelerated Motion :
𝒖 𝒗
s
a
Fig. Velocity-time graph to obtain the equations
From the velocity-time graph (Fig.), the
acceleration of the object is given by,
a = slope of graph
=
𝑩𝑫
𝑨𝑫
=
𝒗 −𝒖
𝒕
Or, 𝒗 = 𝒖 + at …(1)
Fig.

27. (2)EQUATION FOR POSITION-TIME
RELATION (s = 𝒖 t +
𝟏
𝟐
a𝒕𝟐)
Fig. Velocity-time graph to obtain the equations
From the v-t graph the displacement travelled by
the object is given by,
s = area OABC (which is a trapezium)
= area of the rectangle OADC + area of
the triangle ABD
= OA × OC +
𝟏
𝟐
(AD × BD)
= 𝒖 × t +
𝟏
𝟐
(t × at ) (BD = 𝒗 − 𝒖
= at)
Or, s = 𝒖 t +
𝟏
𝟐
a𝒕𝟐 …(2)

28. (3)EQUATION FOR POSITION–VELOCITY
RELATION ( 𝒗𝟐 = 𝒖𝟐 + 2as)
Fig. Velocity-time graph to obtain the
equations
From the v-t graph shown in
Fig., the distance travelled by the object
in time t is given by,
s = area of the trapezium OABC
=
(OA + BC )×OC
𝟐
=
(𝒖+ 𝒗)×𝒕
𝟐
=
(𝒗+ 𝒖)×(𝒗 − 𝒖)
𝟐𝒂
As, { t =
𝒗−𝒖
𝒂
}
Or, 𝒗𝟐 − 𝒖𝟐 = 2as …(iii)