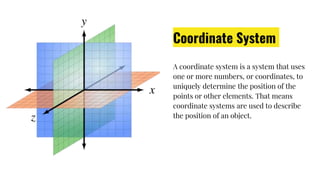
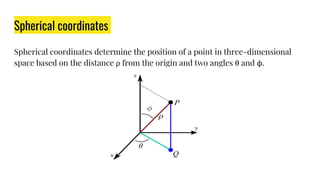
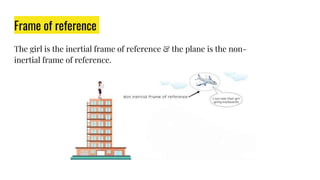
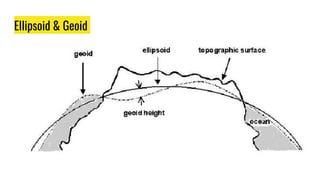
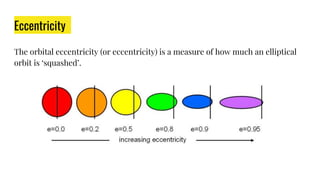
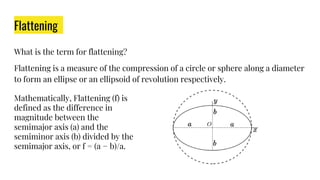
The document provides an overview of various coordinate systems used to determine the position of points or elements, classifying them into categories such as topocentric, geocentric, and more. It discusses specific systems like polar, cylindrical, spherical, and Cartesian coordinates, as well as the geographic coordinate system and the Earth-Centered, Earth-Fixed (ECEF) system. The document also covers concepts like transformation matrices, ellipsoids, geoid, eccentricity, flattening, and the World Geodetic System 1984 (WGS84), which is crucial for GPS navigation.

1. Md. Sajid Hassan
MSc in EECE (Ongoing)
Roll-0422160003
Dept. of EECE
Military Institute of Science &
Technology (MIST)
Coordinate
Systems

2. Coordinate System
A coordinate system is a system that uses
one or more numbers, or coordinates, to
uniquely determine the position of the
points or other elements. That means
coordinate systems are used to describe
the position of an object.

3. Classification According to body of reference and location
of origin:
1. Topocentric
2. Geocentric
3. Heliocentric
4.Selenocentric
Depending on way of coordinate system set it
may be: Polar, Cylindrical, Spherical,
Cartesian etc.

4. Polar Coordinate System
Polar coordinate system is a two-dimensional coordinate system in which each
point on a plane is determined by a distance from a reference point and an angle
from a reference direction.

5. Cylindrical Coordinate System
Cylindrical coordinates can be defined as a set of three coordinates that are used
to locate a point in the cylindrical coordinate system. In two dimensions, the
location of a point can be denoted by both cartesian and polar coordinates.

6. Spherical coordinates
Spherical coordinates determine the position of a point in three-dimensional
space based on the distance ρ from the origin and two angles θ and ϕ.

7. Cartesian coordinates
The Cartesian coordinates (also called rectangular coordinates) of a point are a
pair of numbers (in two-dimensions) or a triplet of numbers (in three-
dimensions) that specified signed distances from the coordinate axis.

8. Geographic coordinate system
A geographic coordinate system is a system that uses a three-dimensional
spherical surface to determine locations on the Earth. Any location on Earth can
be referenced by a point with longitude and latitude coordinates.

9. Earth-centered, Earth-fixed coordinate system
The Earth-centered, Earth-fixed coordinate system (acronym ECEF) is a
geographic and Cartesian coordinate system (sometimes known as a
"conventional terrestrial" system). It represents positions as X, Y, and Z
coordinates. The origin (point 0, 0, 0) is defined as the center of mass of Earth,
hence the term geocentric Cartesian coordinates.

10. Frame of reference
The girl is the inertial frame of reference & the plane is the non-
inertial frame of reference.

11. Inertial Frame of Reference: A frame of reference where Newton's law holds true
is called an inertial frame of reference.
Non-Inertial Frame of Reference: Newton's law will not apply.

12. Coordinate system
conversion A coordinate system conversion is a
conversion from one coordinate system to
another, with both coordinate systems
based on the same geodetic datum.
*Common conversion tasks include
conversion between geodetic and earth-
centered, earth-fixed (ECEF) coordinates
and conversion from one type of map
projection to another.

13. From Geographic (Geodetic) to ECEF coordinates

14. From ECEF to geodetic coordinates

15. Geodetic to/from ENU coordinate
To convert from geodetic coordinates to local tangent plane (ENU) coordinates is
a two-stage process:
1. Convert geodetic coordinates to ECEF coordinates
2. Convert ECEF coordinates to local ENU coordinates

17. Conversion across map projections

18. Datum
transformations

19. Transformation Matrix
Transformation Matrix is a matrix that transforms one vector into another
vector by the process of matrix multiplication.

20. Importance of transformation matrix in coordinate
transformation?
This is a useful property as it allows the transformation of both positional
vectors and normal vectors with the same matrix. For different mathematical
operation in coordinate system following are some of the important applications
of the transformation matrix-
1. Vectors represented in a two or three-dimensional frame are transformed to
another vector.
2. Linear Combinations of two or more vectors through multiplication are
possible through a transformation matrix.

21. 3. The linear transformations of matrices can be used to change the matrices into
another form.
4. Matrix multiplication is the transformation of one matrix into another matrix.
5. Determinants can be solved using the concepts of the transformation matrix.
6. Inverse Space also use matrix transformations.
7. Abstract Vector Spaces also use the concepts of the transformation matrix etc.

22. Ellipsoid & Geoid

23. Ellipsoid: Ellipsoid comes from the word "ellipse," which is simply a
generalization of a circle. Ellipsoids are generalizations of spheres. The Earth is
not a true sphere, it is an ellipsoid, as Earth is slightly wider than it is tall.
Although other models exist, the ellipsoid is the best fit to Earth.
Geoid: Like the ellipsoid, the geoid is a model of the Earth's surface. According to
the University of Oklahoma, "the geoid is a representation of the surface of the
earth that it would assume, if the sea covered the earth." This representation is
also called the "surface of equal gravitational potential," and essentially
represents the "mean sea level." The geoid model is not an exact representation
of sea level surface. Dynamic effects, such as waves and tides, are excluded in the
geoid model.

24. Eccentricity
The orbital eccentricity (or eccentricity) is a measure of how much an elliptical
orbit is ‘squashed’.

25. Flattening
What is the term for flattening?
Flattening is a measure of the compression of a circle or sphere along a diameter
to form an ellipse or an ellipsoid of revolution respectively.
Mathematically, Flattening (f) is
defined as the difference in
magnitude between the
semimajor axis (a) and the
semiminor axis (b) divided by the
semimajor axis, or f = (a − b)/a.

26. Eccentricity & Flattening of Earth
The present eccentricity of Earth is e ≈ 0.01671. In the past, it has varied between
0 and ∼0.06. The eccentricity value can be used to compute the difference in the
distance from Earth to the Sun between their closest and furthest approaches
(perihelion and aphelion); presently, this amounts to 2e ≈ 3.3%. For Earth the
semimajor axis and semiminor axis differ by about 21 kilometres (13 miles),

27. Coordinate System of GPS
The Global Positioning System uses the World Geodetic System (WGS84)
as its reference coordinate system. It consists of a reference ellipsoid, a
standard coordinate system, altitude data, and a geoid. Similar to the
North American Datum of 1983 (NAD83), it uses the Earth's center mass as
the coordinate origin.

28. World Geodetic System 1984
WGS 84 (G1674) follows the criteria outlined in the International Earth Rotation
Service (IERS) Technical Note 21. The WGS 84. Coordinate System origin also
serves as the geometric center of the WGS 84 Ellipsoid and the Z axis serves as
the rotational axis of this ellipsoid of revolution. WGS 84 geodetic coordinates
are
generated by using its reference ellipsoid.

29. WGS 84 identifies four defining parameters. These are the semi-major
axis of the WGS 84 ellipsoid, the flattening factor of the Earth, the nominal mean
angular
velocity of the Earth, and the geocentric gravitational constant as specified
below.

30. The Common Coordinate system used for Navigation
Latitude and longitude, and Universal Transverse Mercator are two global
coordinate systems commonly used.
Previously, we have discussed about latitude and longitude. The remaining
discussions are about UTM.

31. Universal Transverse Mercator
The Universal Transverse Mercator (UTM) is a map projection system for
assigning coordinates to locations on the surface of the Earth. Like the
traditional method of latitude and longitude, it is a horizontal position
representation, which means it ignores altitude and treats the earth as a
perfect ellipsoid.