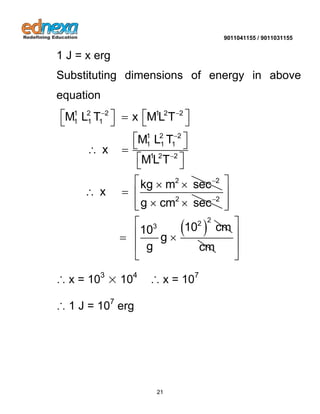
This document discusses the concepts of physical quantities, units, and dimensions in physics. It defines physical quantities as those that can be measured using physical means or apparatus, giving examples like mass, length, and time. Units are defined as standards used to measure physical quantities. Dimensions are used to determine the units of derived quantities by relating them to fundamental quantities and their units using exponents. The document also discusses the S.I. system of units and provides examples of using dimensional analysis to check equations and determine conversion factors between different units.

1. 9011041155 / 9011031155
1
Measurements Physics Physics is a branch of science which deals with study of natural phenomenon of non-living things. Origin “fuses”
Physical quantities
The quantities which can be measured with physical apparatus or physical means are called physical quantities. e.g.mass Length

2. 9011041155 / 9011031155
2
Time Temperature
etc.
Physical quantities are expressed in terms of magnitude and unit. Non – physical quantities
The quantities which cannot be measured with physical apparatus or no physical apparatus is available for their measurement are called non-physical quantities.
e.g. Intelligence of a person, happiness etc.

3. 9011041155 / 9011031155
3
Measurement
Measurement of a physical quantity is its careful and accurate comparison with the standard of that quantity. Unit
The standard used for comparison of a physical quantity is called unit of that quantity. e.g. 1kg

4. 9011041155 / 9011031155
4
Magnitude
Magnitude of a physical quantity is the number which indicates how many times the unit is contained in it. e.g. 10 litres
The physical quantities are classified in to two types
1. Fundamental quantities :- The physical quantities which can be independently measured and expressed are called fundamental quantities. Thus, these quantities can be measured and expressed without taking help of other quantities. e.g. length, mass, time, temperature etc.
Fundamental units :- The units of the fundamental quantities are called fundamental units.

5. 9011041155 / 9011031155
5
e.g. metre, kilogram, second etc. Fundamental quantities
i. length
Metre
(m)
ii. mass
Kilogram
(kg)
iii. time
Seconds
(s)
iv. temperature
Kelvin
(K)
v. Electric current
Ampere
(A)
vi. Luminous Intensity
Candela
(cd)
viii. Amount of substance
Mole
(mol)
Supplementary Quantities i. Plane angle → Radian → rad ii. Solid Angle → Steradian → sr

6. 9011041155 / 9011031155
6
iii. Frequency → 1/t = 1/s = Hertz (Hz)
2. Derived quantities :- The physical quantities which require two or more fundamental quantities for their measurement and expression are called derived quantities.
e.g. speed, acceleration, force etc.
Derived units :- The units of derived quantities are called derived units.
e.g. m/s, m/s2, newton etc.
Requirements of good units
1. The unit should be easy to use and read.
2. Its magnitude should not change with respect to time, temperature, place and observer.
3. It should be easily reproducible. It means, it should be easy to copy and can be produced anywhere any quantity. 4. It should be acceptable worldwide.

7. 9011041155 / 9011031155
7
(universally acceptable ) System of units
The fundamental units together with all derived units form a system of units. Formerly there were different unit systems used in different countries. Some of the most common unit systems were as follows :- 1. C.G.S. 2. M.K.S. 3. F.P.S.
4. S.I.( System International ) :- To avoid difficulties in inter conversions of units and to have uniformity
in the units used all over the world, General Conference of weights and Measures suggested an
improved metric system called System International in 1960. It was accepted by I.S.O.( International
Standards Organization ) in 1962. This includes all the fundamental units from M.K.S. and over 450

8. 9011041155 / 9011031155
8
derived units. As far as possible the units are named after renowned scientists to honour them.
Before the introduction of S.I. exchange of information between the scientists of different
countries was difficult because of the difference between the unit systems used by them. With the worldwide use of S.I. this difficulty is removed.
Now in this common language of units, scientists engineers and technicians all over the world can exchange their ideas, criticism easily. So, this system has bridged-up the gap between them.
Rules of writing S.I. units
1. metre, joule, newton
Metre, Joule,Newton

9. 9011041155 / 9011031155
9
2. cm, m/s, J, N
Cm, M/s, j, n etc. 3. singular form only. plural form of units:- not allowed, e.g. While speaking, we may say that the mass is 100 kilograms,
but while writing, we should write 10kg only and not 10kgs. 4. No punctuation marks
e.g. the unit newton metre should be written as Nm and not like N-m or N,m etc. m/s is a valid unit because the slash (/) is not a punctuation mark. It is a mathematical operator.

10. 9011041155 / 9011031155
10
Dimensions
Increasing the power of fundamental units to find out
units of derived quantities is known as dimensions.
1.
0 1 1
displacement
Velocity
Time
V
T
[ M L T ] m / s 


 
l
2. Area = ℓ2
= [ M0 L2 T0] = m2
3. Volume = ℓ3
= [ M0L3T0] = m3

11. 9011041155 / 9011031155
11
4.
2
0 1 2 2
V / T
Acceleration
T T
T
M LT m / s 
 

   
l
l
5. Force = ma
= m × ℓ / T2
= [ M1L1T-2] = kg m / s2 = N
6. Work = F . ℓ
= ma . ℓ
= m . ℓ / T2 . ℓ
= m . ℓ2 / T2
= [ M1 L2 T-2] = kg . m / s2 = J

12. 9011041155 / 9011031155
12
7.
2
2
2 2
1 1 2 2
Force
Pr essure
Area
ma
m. / T m
.T
M L T kg m / s  


 
   
l
l
l l
8.
2
2
1 2 3 2 3
3
Work
Power
Time
F .
T
ma .
T
m . / T .
T
m
M L T kgm / s w
T





     
l
l
l l
l

13. 9011041155 / 9011031155
13
9. P.E = mgh
2
1 2 2 2 2
m. / T .
M L T kgm / s J 

    
l l
10.
2
2 2
1 2 2 2 2
1
K.E mv
2
1
m. / t
2
[M L T ] kgm / s J 


  
l
11. Impulse = F.T
= ma . T
= m . ℓ / T2 . T
2
1 1 1
m. . T
T
MLT kg m / s Ns 

    
l

14. 9011041155 / 9011031155
14
12. Momentum = mv
= m . ℓ / T
= [ M1 L1T-1 ]
= kg m / s
13.
3
1 3 0 3
mass
Density
Volume
m
ML T kg/m 


   
l
M = [ M1L0T0]
ℓ = [ M0L1T0]
T = [ M0L0T1]

15. 9011041155 / 9011031155
15
Uses of dimensional analysis
1. To check correctness of equation.
principle of homogeneity:- It states that dimensions
towards both sides of equation for each term are
same. Then the given equation is dimensionally
correct.
For e.g.
1. 2 1
s ut at
2
 
s is displacement
u = initial velocity
t = time
a = acceleration
L.H.S = ∴ S = [ M0L0T1] ….. (1)
R.H.S

16. 9011041155 / 9011031155
16
∴ ut = [ M0L1T-1] [ M0L0T1]
= [ M0L1+0T-1+1]
= [ M0L1T0] …… (2)
2 1
at
2
= [ M0L1T-2] [ M0L0T1]2
= [ M0L1T-2] [ M0L0T2]
= [ M0L1T0] …….. (3)
From (1), (2) & (3) we can say that the given
equation is dimensionally correct.
2. v2 = u2 + 2as
3. v = u + at
4. w = w0 + mc2
w = work
w0 = work
m = mass
c = speed of light

17. 9011041155 / 9011031155
17
2. To find out conversion factor in between different
units of same quantity .
e.g.1 Let MKS unit of force if Newton (N)
CGS unit of force is Dyne
Let 1 N = x dyne
Substituting dimensions of force in above
equation,
1 1 2 1 1 2
1 1 1
1 1 2
1 1 1
1 1 2
2
M L T x MLT
ML T
x
MLT
kg m s
 



    
   
 
 

2 g cm s  
3 2
3 2
5
5
10 10 cm
g
g cm
10 10
x 10
1N 10 dyne
 
 
 
 
   
 
 
 
 
1 J = x erg

18. 9011041155 / 9011031155
18
e.g.2 v = u + at v = final velocity u = initial velocity a = acceleration t = time L.H.S = v ∴ v = [ M0L1T-1] ……… (1) R.H.S = u ∴ u = [ M0L1T-1] ……… (2) R.H.S at = [ M0L1T-2] [ M0L0T1] = [ M0L1T-1] ………… (3) From (1), (2), (3) we can say that the given equation is dimensionally correct.

19. 9011041155 / 9011031155
19
e.g. 3 v2 = u2 + 2as v = final velocity u = initial velocity a = acceleration s = displacement L.H.S = v2 ∴ v2 = [ M0L1T-1]2 = [ M0L1T-1] …….. (1) R.H.S = u2 ∴ u2 = [ M0L1T-1] 2 = [ M0L2T-2] …….. (2) as = [ M0L1T-2] [ M0L1T0] = [ M0L1+1 T-2+0] = [ M0L2T-2] …….. (3)

20. 9011041155 / 9011031155
20
From (1), (2), & (3) we can say that the given equation is dimensionally correct. e.g.4 w = w0 + mc2 w = work w0 = work m = mass c = speed of light L.H.S = w ∴ w = [ M1L2T-2] ……… (1) R.H.S = w0 + mc2 w0 = [ M1L2T-2] ……… (2) mc2 = [ M1L0T0] [ M0L1T-1]2 = [M1L0T0] [M0L2T-2] = [M1L0+2 T0-2] = [M1L2T-2]
From (1), (2), & (3) we can say that the given equation is dimensionally correct.

21. 9011041155 / 9011031155
21
1 J = x erg
Substituting dimensions of energy in above
equation
1 2 2 1 2 2
1 1 1
1 2 2
1 1 1
1 2 2
2 2
M L T x ML T
M L T
x
ML T
kg m sec
x
 



    
   
 
 
 
2 2 g cm sec  
 2
3 102 cm 10
g
g
 
 
 
 
cm
 
 
 
 
∴ x = 103 × 104 ∴ x = 107
∴ 1 J = 107 erg

22. 9011041155 / 9011031155
22
• Ask Your Doubts • For inquiry and registration, call 9011041155 / 9011031155.