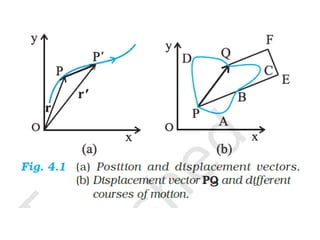
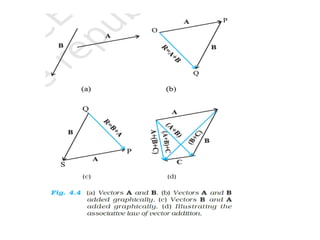
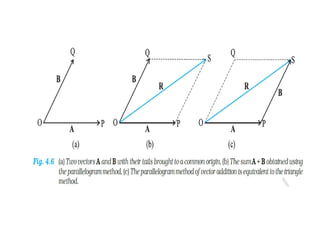
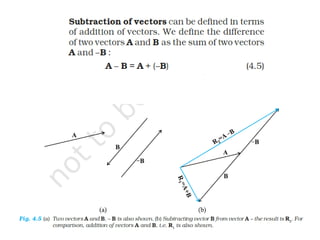
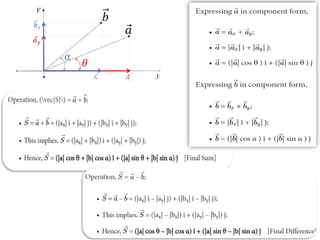
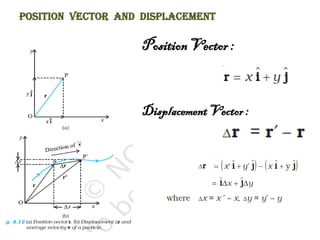
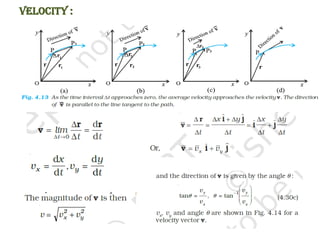
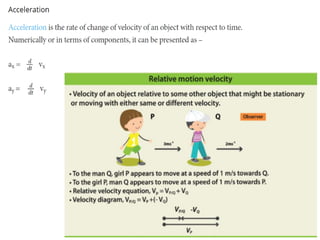
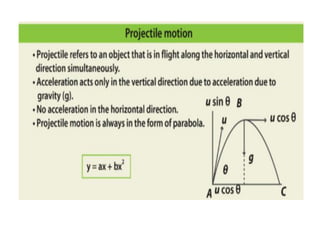
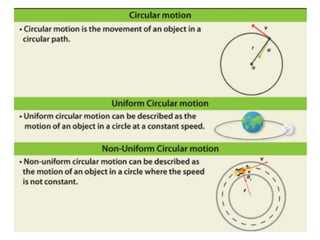
The document provides key concepts related to motion in a plane, including definitions of scalar and vector quantities, position and displacement vectors, and various vector properties such as modulus, unit, and null vectors. It also explains vector addition through the triangle and parallelogram laws, and discusses the resolution of vectors into components along the x and y axes. Additionally, it details basic definitions related to projectile motion, including the nature of projectiles, maximum height, time of flight, and horizontal range.

1. MOTION IN A PLANE
CLASS XI

2. IMPORTANT TERMS
1. SCALAR AND VECTOR QUANTITIES
a) Scalar Quantity: The physical quantities which are
completed specified by their magnitude only are
called scalar quantities.
Eg: Temperature, Mass, length, time, work…
b) Vector Quantity: The physical quantities which have
both magnitude and direction are called vector
quantities.
Eg: Displacement, Velocity, Acceleration…

3. 2. Position and displacement Vector
a) Position Vector: A vector drawn from the origin to the
position of a particle at any instant is called position
vector.
Eg: Consider an object is moving in x-y plane with origin at O.
Suppose an object is at point A at any instant t. Then OA is
the position vector of the object at point A.
b) Displacement Vector: The displacement vector of a
moving particle in a given interval of time is a direct line
segment from the initial to the final position of the
particle.
Eg: Consider an object moving in the x-y plane. Suppose it is at
a point A at any instant t and at point B at any instant t’.
then the vector AB is the displacement vector of the
object in the time t to t’.

5. IMPORANT DEFINITION RELATED TO
VECTORS
1. Modulus of a vector: The magnitude of a vector
is called modulus of a vector. For a vector A it is
represented by |A|.
2. Unit vector: A vector having magnitude equal to
unity but having a specific direction is called a
unit vector.
3. Null Vector: A vector with magnitude zero and
having an arbitrary direction is called a null
vector.
4. Equal Vector: Two vectors are said to be equal if
they have equal magnitude and same direction.

6. 5. Negative Vector: Two vectors are said to be
negative of each other if their magnitude are
equal but direction are opposite.
6. Collinear Vectors: The two or more vectors
are said to be collinear, when they act along
the same lines or parallel lines.

7. ADDITION OF VECTORS
1. Triangle law of vector addition:
If two vectors are represented both in
magnitude and direction by the two sides of
a triangle taken in the same order then the
resultant of these vectors is represented both
in magnitude and direction by the third side
of the triangle taken in the opposite order.

9. 2. Parallelogram law of vector addition:
If two vectors are represented both in
magnitude and direction by the adjacent sides
of a parallelogram drawn from a point then
the resultant vector is represented both in
magnitude and direction by the diagonal of
the parallelogram passing through the same
point.

14. RESOLUTION OF VECTORS
A vector can be resolved into many different
vectors, for resolution of vectors.
For Example: Let us consider two numbers,
say, 4 and 6, which is further added to obtain
10. Further, now 10 is broken or resolved.
However, the number 10 can also be
resolved into many other numbers like
–10 = 5 + 5; 10 = 3 + 7 etc.
Resolution of a vector is the splitting of a
single vector into two or more
components in different directions which
together produces a similar effect as is
produced by a single vector itself. The
vectors formed after splitting are called
component vectors.
Resolution of a vector is the splitting of a
single vector into two or more components in
different directions which together produces
a similar effect as is produced by a single
vectoritself.
The vectors formed after splitting are
called component vectors.

15. RESOLVING VECTORS ALONG X AND Y AXIS
The complete figure seems to be like a
Parallelogram, further applying the
Parallelogram law of vector addition. Herein,
the two vectors ax and ay appears to be added
by the parallelogram law of vector addition to
obtain vector a . Therefore, with this, we can
say that ax and ay are the resolved output
of ax as ay has been again broken back to its
components. Here,
• ax is the x-component; and
• ay is the y-component of a.

17. Position Vector and Displacement
Position Vector :
DisplacementVector:

18. Velocity :

24. DEFINITION RELATED TO PROJECTILE
MOTION
1. Projectile: An object with initial velocity and
which is then allowed to move under the
action of gravity along is called a projectile.
2. Maximum height attend by a projectile: The
maximum vertical distance travelled by a
projectile during its journey is called
maximum height attend by a projectile. It is
represented by ‘H’.

25. 3. Time of flight: Total time taken by the
projectile from the point of projection till it
hits the horizontal plane having point of
projection is called time of flight.
4. Horizontal Range of projectile: The maximum
horizontal distance between the point of
projection and the point on the horizontal
plane where the projectile hits is called
horizontal range.