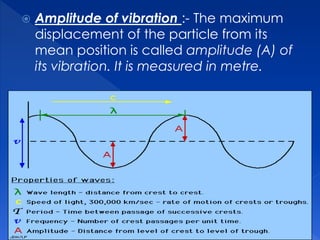
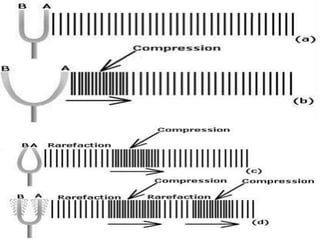
The document discusses different types of motions including translational, rotational, oscillatory, and vibrational motion. It also defines key terms related to oscillations such as period, frequency, amplitude, damped oscillations, and sustained oscillations. Regarding waves, it describes longitudinal and transverse waves, and defines properties such as wavelength, velocity, and how velocity is related to frequency and wavelength. It also provides formulas for calculating the velocity of longitudinal and transverse waves in different media.

2.  Displacement of a particle or energy
from one point to anther point is known
as motion.

4.  Translational motion :-
the body moves along a straight line
path or along a curved path.
e.g. motion of a train, car, crawling if
insects etc.

5.  the body moves round and round along
a circular path about an axis.
e.g. motion of the blades of an electric
fan, spinning top, merry-go-round etc.

6.  Oscillatory or Vibrational motion :- the object
moves to and fro, tracing the same path
again and again in equal intervals of time.
e.g. motion of a swing, needle of a sewing
machine, prongs of a tuning fork etc.

7.  Oscillator or Vibrator :- The particle
performing oscillatory motion is called
oscillator or vibrator.
 Oscillation :- During oscillatory motion
the oscillator performs number of same
sets of vibration, in equal intervals of
time One such set of vibration is called
oscillation.

8.  Periodic time or Period of oscillation :-
The time taken by the particle to perform
one oscillation is called period of
oscillation (T).
It is measured in second.
 Frequency of oscillation :-
Number of oscillations performed by the
particle in one second is called
frequency of oscillation (n).
It is measured in hertz (Hz)

9.  Amplitude of vibration :- The maximum
displacement of the particle from its
mean position is called amplitude (A) of
its vibration. It is measured in metre.

10.  Damped oscillations :- Generally when an
object is set in to oscillations, it starts moving
to and fro. During its motion it has to
overcome the air resistance. For this, it has
to spend energy. Thus, the energy of the
particle goes on decreasing, which
decreases its amplitude. So, after some
time the object stops moving. Such
oscillations are called damped oscillations.
 Sustained Oscillations :- If energy is
continuously supplied to the oscillator, the
amplitude of oscillations remains constant.
Such oscillations of constant amplitude are
called sustained oscillations.

11. What is sound?

12.  Energy or matter?Wave

13.  The motion of the oscillatory disturbance
through a medium is called wave motion.

14.  Wave is defined as the oscillatory
disturbance travelling through a
medium without change of form.

15.  When a wave travel through a medium,
it is observed that at any given point of
the medium, the form of the wave
repeats from time to time, which shows
that the wave is periodic in time.
 Also at any instant of time, the form of
waves repeats at equal distances,
which shows that it is periodic in space.

16. 
Waves
Mechanical
progressive Stationary
Electromagnetic

17. Mechanical waves :- The waves which
require material medium for their
propagation are called mechanical
waves. e.g. sound waves.
Non Mechanical waves :- The waves
which does not require material medium
for their propagation are called
mechanical waves. e.g. Light waves.

18. 1. The medium should be elastic
2. The medium should possess
3. The frictional resistance of the medium
should be small

19.  The waves which travel in the same
direction continuously are called
progressive waves.

20. progressive
Transverse Longitudinal

21.  The waves in which the particles of
the medium vibrate in a direction
perpendicular to the direction of
propagation of the wave are called
transverse waves.


22. 1. When the transverse waves travel through a
medium the particles of the medium vibrate in a
direction perpendicular to the direction of
propagation of the waves.
2. The period and the amplitude of vibration of all
the particles is same.
3. When a transverse wave travels through
medium, the medium is divided in to alternate
crests and troughs. The convex part of the wave
is called crest and the concave part is called
trough.

23. 4. One crest and one trough forms wave. The
distance between two consecutive crest or
trough is called wavelength (λ) of the wave.
5. At every point in the medium the crests and
the troughs are alternately produced and they
follow each other as the wave propagates.
6. For the propagation of transverse waves the
medium should possess elasticity of shape.
transverse wave can pass only through solids
and can not propagate through liquids or
gases.

24. 7. The velocity of transverse wave travelling
through stretched string is given by
8. When transverse wave prorogate through
the medium The pressure and density of
medium will remain constant

T
v
M

25. The waves in which the particles of the
medium vibrate in a direction parallel to
the direction of propagation of the wave
are called Longitudinal waves.

27.  Longitudinal wave

28. 1. When the longitudinal waves travel through a
medium the particles of the medium vibrate in
a direction parallel to the direction of
propagation of the waves.
2. The period and the amplitude of vibration of all
the particles is same.
3. When a longitudinal wave travels through
medium, the medium is divided in to alternate
compressions and rarefactions. The denser part
of the wave is called compression and the rare
part is called rarefaction.

29. 4. One compression and one rarefaction forms one
wave. The distance between two consecutive
compressions or rarefactions is called wavelength (λ)
of the wave.
5. At every point in the medium the rarefactions and
the compressions are alternately produced and they
follow each other as the wave propagates.
6. For the propagation of longitudinal waves the
medium
should possess elasticity of volume or bulk modulus,
i.e. it should be able to regain its original volume after
the waves have passed. All solids, liquids and gases
possess elasticity of shape. So, longitudinal wave can
pass through all of them.

30.  Q.1 The longitudinal wave travels in a medium along the
positive direction of X-axis, the particles of the medium
vibrates
(a.1) along Y- axis (b.1) along X–axis
(c.1) along Z-axis (d.1) along any direction
 Q.2 The material medium required for the propagation of
mechanical wave must posses
(a.2) Elasticity (b.2) Inertia
(c.2) Small frictional resistance (d.2) All of these
 Q.3 Longitudinal waves can’t travel through ________
(a.3) Solid (b.3) Liquid
 (c.3) Vacuum (d.3) Gas

31.  (b.1) along X–axis
 (d.2) All of these
 (c.3) Vacuum

32. 7. The velocity of longitudinal wave
travelling through medium is given by
8. When transverse wave prorogate
through the medium The pressure and
density of medium will vary.


E
V

33.  In one oscillation, a wave travels a
distance of one wavelength (λ). For one
oscillation, it takes periodic time (T).
Hence, velocity (v) of the wave is given
as
distance λ
velocity = ---------- = ---
Time T
but 1/T = frequency n of the wave

34. v = nλ

35. Newton’s an empirical formula for this
velocity as :
Where E and ρ are the elasticity and
density of the medium.


E
ForSolids V

36. For gaseous media, (isothermal) .
At N.T.P. P = 1.013 x 105 N/m2 and
ρ= 1.293 kg/m3, v = 280m/s. But,
the practically observed value of speed
of sound in air at N.T.P. is 331 m/s
28% less than the actual value.


P
V

37. Laplace’s Correction :-
According to Laplace, the volumetric changes, that are
taking place during propagation of sound, are adiabatic
and not isothermal. So, elasticity E should be replaced by γP
instead of P, where γ is the
ratio of molar specific heat capacity of the gas at constant
pressure (CP) to its molar specific heat capacity at constant
volume (CV). Thus,
For air the value of g is 1.4. Substituting this value for E, we
get the speed of sound in air as 331m/s, which is in perfect
agreement with the practical value. Hence, the above
modification is called Laplace’s correction and the formula
is called Laplace’s corrected formula for velocity of sound.

  

P
V
CP
v where
C