JL
Uploaded byJimbo Lamb
PDF, PPTX1,899 views

Geometry Section 5-2 1112

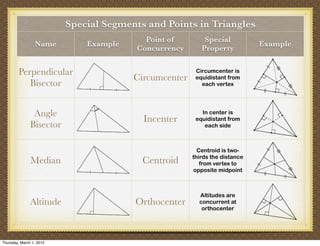
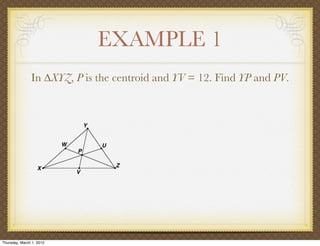
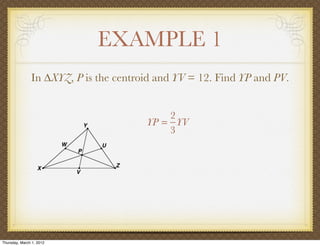
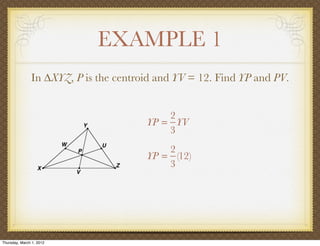
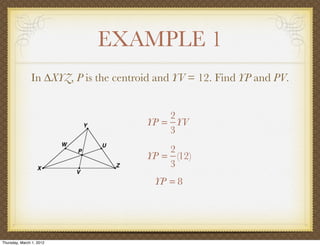
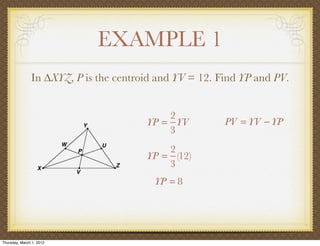
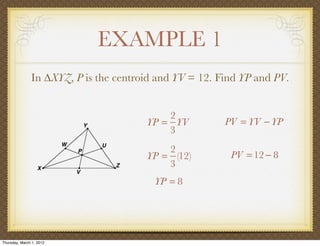
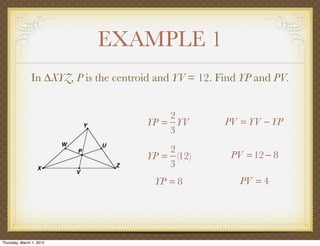
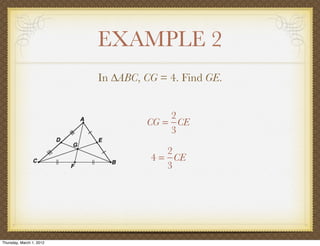
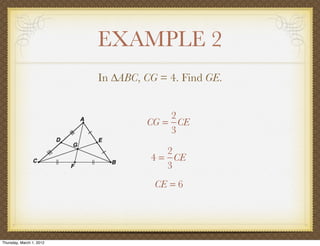
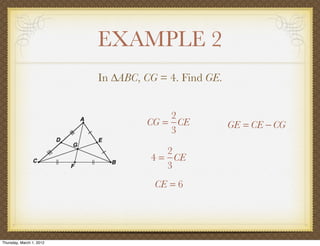
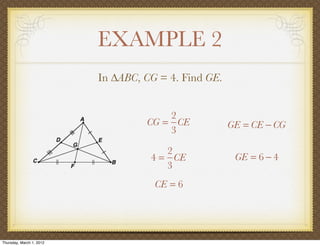
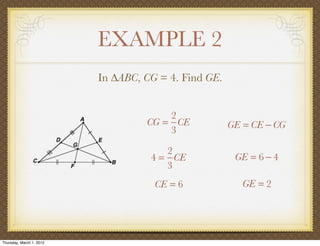
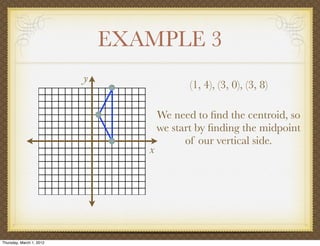
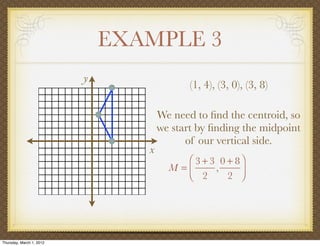
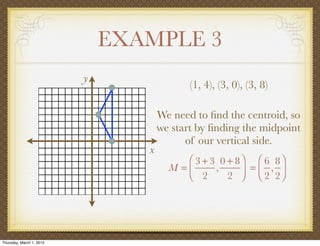
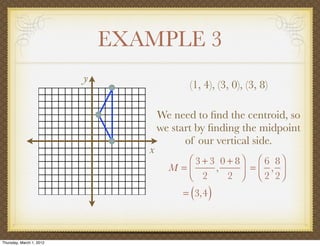
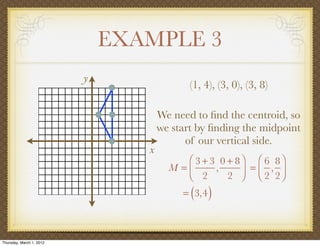
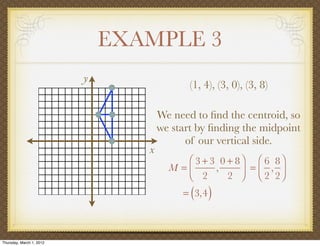
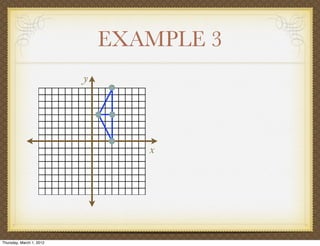
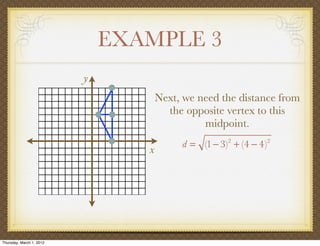
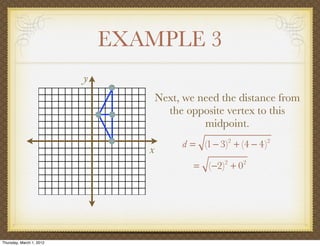
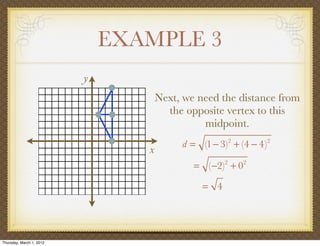
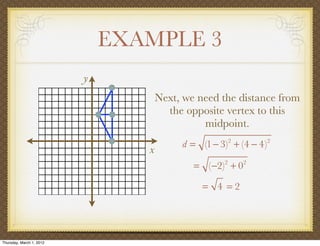
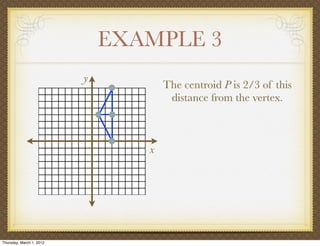
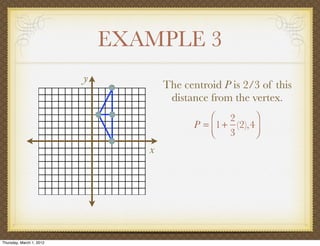
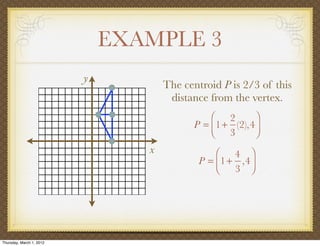
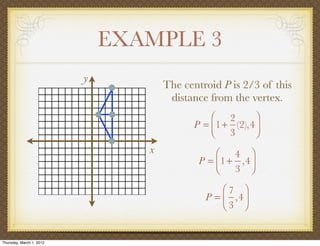
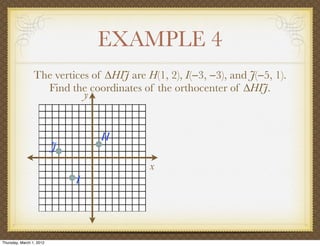
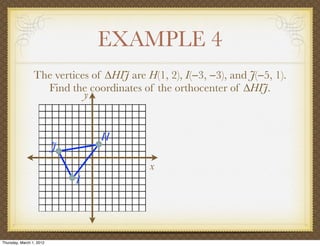
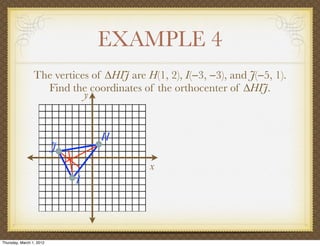
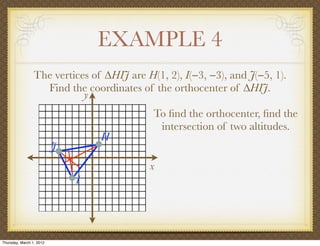
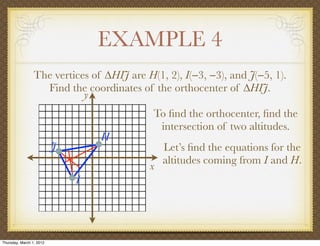
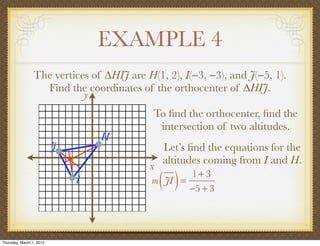
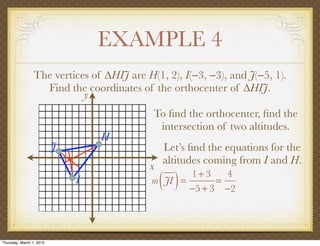
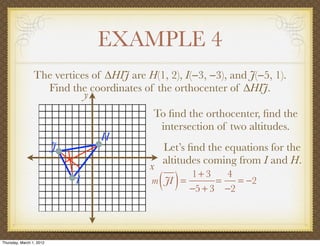
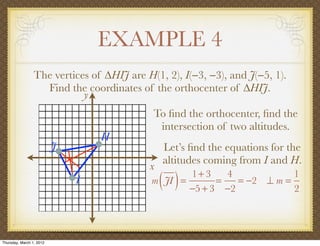
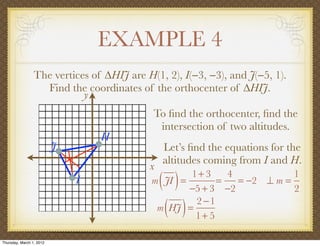
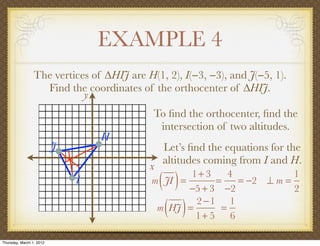
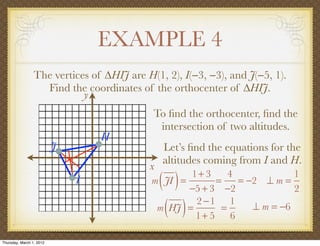
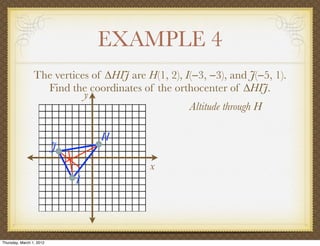
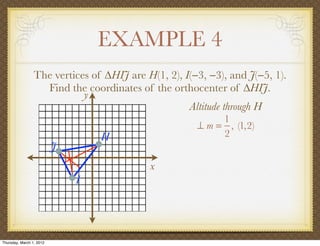
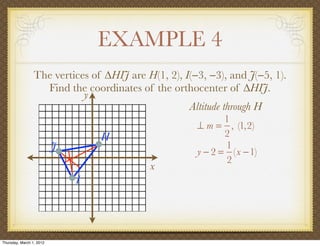
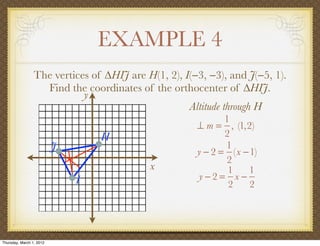
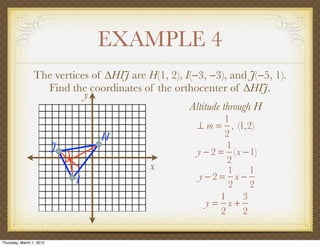
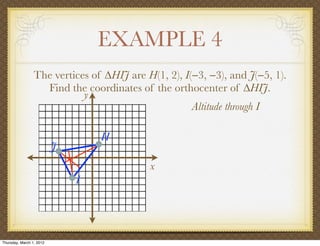
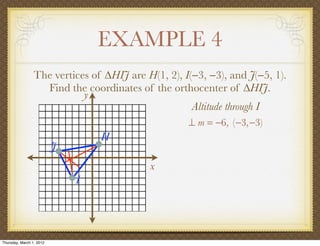
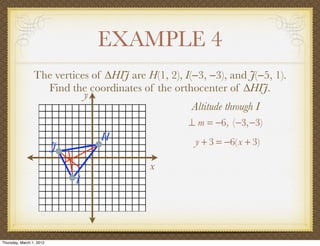
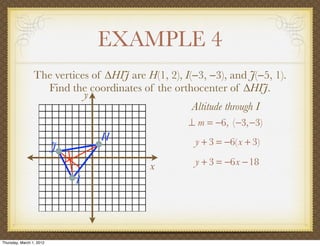
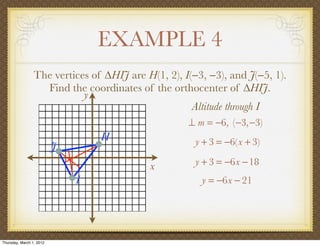
The document discusses medians and altitudes of triangles. It defines key terms like median, centroid, altitude and orthocenter. A median connects a vertex to the midpoint of the opposite side, while an altitude connects a vertex perpendicular to the opposite side. The centroid is the point where the medians intersect and is always inside the triangle. The orthocenter is the point where the altitudes intersect. Examples are provided to demonstrate calculating lengths and finding points related to medians, altitudes, centroids and orthocenters using given information about triangles.

Embed presentation

Download as PDF, PPTX
SECTION 5-2 Medians and Altitudes of Triangles Thursday, March 1, 2012
ESSENTIAL QUESTIONS How do you identify and use medians in triangles? How do you identify and use altitudes in triangles? Thursday, March 1, 2012
VOCABULARY 1. Median: 2. Centroid: 3. Altitude: 4. Orthocenter: Thursday, March 1, 2012
VOCABULARY 1. Median: A segment in a triangle that connects a vertex to the midpoint of the opposite side 2. Centroid: 3. Altitude: 4. Orthocenter: Thursday, March 1, 2012
VOCABULARY 1. Median: A segment in a triangle that connects a vertex to the midpoint of the opposite side 2. Centroid: The point of concurrency where the medians intersect in a triangle (always inside) 3. Altitude: 4. Orthocenter: Thursday, March 1, 2012
VOCABULARY 1. Median: A segment in a triangle that connects a vertex to the midpoint of the opposite side 2. Centroid: The point of concurrency where the medians intersect in a triangle (always inside) 3. Altitude: A segment in a triangle that connects a vertex to the opposite side so that the side and altitude are perpendicular 4. Orthocenter: Thursday, March 1, 2012
VOCABULARY 1. Median: A segment in a triangle that connects a vertex to the midpoint of the opposite side 2. Centroid: The point of concurrency where the medians intersect in a triangle (always inside) 3. Altitude: A segment in a triangle that connects a vertex to the opposite side so that the side and altitude are perpendicular 4. Orthocenter: The point of concurrency where the altitudes of a triangle intersect Thursday, March 1, 2012
5.7 - CENTROID THEOREM The centroid of a triangle is two-thirds the distance from each vertex to the midpoint of the opposite side Thursday, March 1, 2012
5.7 - CENTROID THEOREM The centroid of a triangle is two-thirds the distance from each vertex to the midpoint of the opposite side If G is the centroid of ∆ABC, then 2 2 2 AG = AF , BG = BD, and CG = CE 3 3 3 Thursday, March 1, 2012
Special Segments and Points in Triangles Point of Special Name Example Example Concurrency Property Perpendicular Circumcenter is Circumcenter equidistant from Bisector each vertex Angle In center is Incenter equidistant from Bisector each side Centroid is two- thirds the distance Median Centroid from vertex to opposite midpoint Altitudes are Altitude Orthocenter concurrent at orthocenter Thursday, March 1, 2012
EXAMPLE 1 In ∆XYZ, P is the centroid and YV = 12. Find YP and PV. Thursday, March 1, 2012
EXAMPLE 1 In ∆XYZ, P is the centroid and YV = 12. Find YP and PV. 2 YP = YV 3 Thursday, March 1, 2012
EXAMPLE 1 In ∆XYZ, P is the centroid and YV = 12. Find YP and PV. 2 YP = YV 3 2 YP = (12) 3 Thursday, March 1, 2012
EXAMPLE 1 In ∆XYZ, P is the centroid and YV = 12. Find YP and PV. 2 YP = YV 3 2 YP = (12) 3 YP = 8 Thursday, March 1, 2012
EXAMPLE 1 In ∆XYZ, P is the centroid and YV = 12. Find YP and PV. 2 YP = YV PV = YV − YP 3 2 YP = (12) 3 YP = 8 Thursday, March 1, 2012
EXAMPLE 1 In ∆XYZ, P is the centroid and YV = 12. Find YP and PV. 2 YP = YV PV = YV − YP 3 2 YP = (12) PV = 12 − 8 3 YP = 8 Thursday, March 1, 2012
EXAMPLE 1 In ∆XYZ, P is the centroid and YV = 12. Find YP and PV. 2 YP = YV PV = YV − YP 3 2 YP = (12) PV = 12 − 8 3 YP = 8 PV = 4 Thursday, March 1, 2012
EXAMPLE 2 In ∆ABC, CG = 4. Find GE. Thursday, March 1, 2012
EXAMPLE 2 In ∆ABC, CG = 4. Find GE. 2 CG = CE 3 Thursday, March 1, 2012
EXAMPLE 2 In ∆ABC, CG = 4. Find GE. 2 CG = CE 3 2 4 = CE 3 Thursday, March 1, 2012
EXAMPLE 2 In ∆ABC, CG = 4. Find GE. 2 CG = CE 3 2 4 = CE 3 CE = 6 Thursday, March 1, 2012
EXAMPLE 2 In ∆ABC, CG = 4. Find GE. 2 CG = CE GE = CE − CG 3 2 4 = CE 3 CE = 6 Thursday, March 1, 2012
EXAMPLE 2 In ∆ABC, CG = 4. Find GE. 2 CG = CE GE = CE − CG 3 2 4 = CE GE = 6 − 4 3 CE = 6 Thursday, March 1, 2012
EXAMPLE 2 In ∆ABC, CG = 4. Find GE. 2 CG = CE GE = CE − CG 3 2 4 = CE GE = 6 − 4 3 CE = 6 GE = 2 Thursday, March 1, 2012
EXAMPLE 3 An artist is designing a sculpture that balances a triangle on tip of a pole. In the artistʼs design on the coordinate plane, the vertices are located at (1, 4), (3, 0), and (3, 8). What are the coordinates of the point where the artist should place the pole under the triangle so that is will balance? Thursday, March 1, 2012
EXAMPLE 3 (1, 4), (3, 0), (3, 8) Thursday, March 1, 2012
EXAMPLE 3 y (1, 4), (3, 0), (3, 8) x Thursday, March 1, 2012
EXAMPLE 3 y (1, 4), (3, 0), (3, 8) x Thursday, March 1, 2012
EXAMPLE 3 y (1, 4), (3, 0), (3, 8) x Thursday, March 1, 2012
EXAMPLE 3 y (1, 4), (3, 0), (3, 8) We need to find the centroid, so we start by finding the midpoint of our vertical side. x Thursday, March 1, 2012
EXAMPLE 3 y (1, 4), (3, 0), (3, 8) We need to find the centroid, so we start by finding the midpoint of our vertical side. x ⎛ 3 + 3 0 + 8⎞ M =⎜ , ⎟ ⎝ 2 2 ⎠ Thursday, March 1, 2012
EXAMPLE 3 y (1, 4), (3, 0), (3, 8) We need to find the centroid, so we start by finding the midpoint of our vertical side. x ⎛ 3 + 3 0 + 8⎞ ⎛ 6 8⎞ M =⎜ , ⎟ = ⎜ 2 , 2⎟ ⎝ 2 2 ⎠ ⎝ ⎠ Thursday, March 1, 2012
EXAMPLE 3 y (1, 4), (3, 0), (3, 8) We need to find the centroid, so we start by finding the midpoint of our vertical side. x ⎛ 3 + 3 0 + 8⎞ ⎛ 6 8⎞ M =⎜ , ⎟ = ⎜ 2 , 2⎟ ⎝ 2 2 ⎠ ⎝ ⎠ ( ) = 3,4 Thursday, March 1, 2012
EXAMPLE 3 y (1, 4), (3, 0), (3, 8) We need to find the centroid, so we start by finding the midpoint of our vertical side. x ⎛ 3 + 3 0 + 8⎞ ⎛ 6 8⎞ M =⎜ , ⎟ = ⎜ 2 , 2⎟ ⎝ 2 2 ⎠ ⎝ ⎠ ( ) = 3,4 Thursday, March 1, 2012
EXAMPLE 3 y (1, 4), (3, 0), (3, 8) We need to find the centroid, so we start by finding the midpoint of our vertical side. x ⎛ 3 + 3 0 + 8⎞ ⎛ 6 8⎞ M =⎜ , ⎟ = ⎜ 2 , 2⎟ ⎝ 2 2 ⎠ ⎝ ⎠ ( ) = 3,4 Thursday, March 1, 2012
EXAMPLE 3 y x Thursday, March 1, 2012
EXAMPLE 3 y Next, we need the distance from the opposite vertex to this midpoint. x Thursday, March 1, 2012
EXAMPLE 3 y Next, we need the distance from the opposite vertex to this midpoint. d = (1 − 3)2 + (4 − 4)2 x Thursday, March 1, 2012
EXAMPLE 3 y Next, we need the distance from the opposite vertex to this midpoint. d = (1 − 3)2 + (4 − 4)2 x = (−2) + 0 2 2 Thursday, March 1, 2012
EXAMPLE 3 y Next, we need the distance from the opposite vertex to this midpoint. d = (1 − 3)2 + (4 − 4)2 x = (−2) + 0 2 2 = 4 Thursday, March 1, 2012
EXAMPLE 3 y Next, we need the distance from the opposite vertex to this midpoint. d = (1 − 3)2 + (4 − 4)2 x = (−2) + 0 2 2 = 4 =2 Thursday, March 1, 2012
EXAMPLE 3 y x Thursday, March 1, 2012
EXAMPLE 3 y The centroid P is 2/3 of this distance from the vertex. x Thursday, March 1, 2012
EXAMPLE 3 y The centroid P is 2/3 of this distance from the vertex. ⎛ 2 ⎞ P = ⎜1 + (2),4 ⎟ ⎝ 3 ⎠ x Thursday, March 1, 2012
EXAMPLE 3 y The centroid P is 2/3 of this distance from the vertex. ⎛ 2 ⎞ P = ⎜1 + (2),4 ⎟ ⎝ 3 ⎠ x ⎛ 4 ⎞ P = ⎜1 + ,4 ⎟ ⎝ 3 ⎠ Thursday, March 1, 2012
EXAMPLE 3 y The centroid P is 2/3 of this distance from the vertex. ⎛ 2 ⎞ P = ⎜1 + (2),4 ⎟ ⎝ 3 ⎠ x ⎛ 4 ⎞ P = ⎜1 + ,4 ⎟ ⎝ 3 ⎠ ⎛7 ⎞ P = ⎜ ,4 ⎟ ⎝3 ⎠ Thursday, March 1, 2012
EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. Thursday, March 1, 2012
EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y x Thursday, March 1, 2012
EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y H J x I Thursday, March 1, 2012
EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y H J x I Thursday, March 1, 2012
EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y H J x I Thursday, March 1, 2012
EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y To find the orthocenter, find the intersection of two altitudes. H J x I Thursday, March 1, 2012
EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y To find the orthocenter, find the intersection of two altitudes. H J Let’s find the equations for the altitudes coming from I and H. x I Thursday, March 1, 2012
EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y To find the orthocenter, find the intersection of two altitudes. H J Let’s find the equations for the altitudes coming from I and H. x I ( ) m JI = 1+ 3 −5 + 3 Thursday, March 1, 2012
EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y To find the orthocenter, find the intersection of two altitudes. H J Let’s find the equations for the altitudes coming from I and H. x I ( ) m JI = 1+ 3 = 4 −5 + 3 −2 Thursday, March 1, 2012
EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y To find the orthocenter, find the intersection of two altitudes. H J Let’s find the equations for the altitudes coming from I and H. x I ( ) m JI = 1+ 3 = 4 −5 + 3 −2 = −2 Thursday, March 1, 2012
EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y To find the orthocenter, find the intersection of two altitudes. H J Let’s find the equations for the altitudes coming from I and H. x I ( ) m JI = 1+ 3 = 4 −5 + 3 −2 = −2 ⊥ m = 1 2 Thursday, March 1, 2012
EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y To find the orthocenter, find the intersection of two altitudes. H J Let’s find the equations for the altitudes coming from I and H. x I ( ) m JI = 1+ 3 = 4 −5 + 3 −2 = −2 ⊥ m = 1 2 ( ) m HJ = 2 −1 1+ 5 Thursday, March 1, 2012
EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y To find the orthocenter, find the intersection of two altitudes. H J Let’s find the equations for the altitudes coming from I and H. x I ( ) m JI = 1+ 3 = −5 + 3 −2 4 = −2 ⊥ m = 1 2 ( ) m HJ = 2 −1 1 1+ 5 6 = Thursday, March 1, 2012
EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y To find the orthocenter, find the intersection of two altitudes. H J Let’s find the equations for the altitudes coming from I and H. x I ( ) m JI = 1+ 3 = −5 + 3 −2 4 = −2 ⊥ m = 1 2 ( ) m HJ = 2 −1 1 1+ 5 6 = ⊥ m = −6 Thursday, March 1, 2012
EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y Altitude through H H J x I Thursday, March 1, 2012
EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y Altitude through H 1 ⊥ m = , (1,2) H 2 J x I Thursday, March 1, 2012
EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y Altitude through H 1 ⊥ m = , (1,2) H 2 J 1 y − 2 = (x −1) 2 x I Thursday, March 1, 2012
EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y Altitude through H 1 ⊥ m = , (1,2) H 2 J 1 y − 2 = (x −1) 2 x 1 1 I y−2= x − 2 2 Thursday, March 1, 2012
EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y Altitude through H 1 ⊥ m = , (1,2) H 2 J 1 y − 2 = (x −1) 2 x 1 1 I y−2= x − 2 2 1 3 y= x+ 2 2 Thursday, March 1, 2012
EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y Altitude through I H J x I Thursday, March 1, 2012
EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y Altitude through I ⊥ m = −6, (−3,−3) H J x I Thursday, March 1, 2012
EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y Altitude through I ⊥ m = −6, (−3,−3) H y + 3 = −6(x + 3) J x I Thursday, March 1, 2012
EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y Altitude through I ⊥ m = −6, (−3,−3) H y + 3 = −6(x + 3) J x y + 3 = −6x −18 I Thursday, March 1, 2012
EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y Altitude through I ⊥ m = −6, (−3,−3) H y + 3 = −6(x + 3) J x y + 3 = −6x −18 I y = −6x − 21 Thursday, March 1, 2012
EXAMPLE 4 Thursday, March 1, 2012
EXAMPLE 4 1 3 −6x − 21 = x + 2 2 Thursday, March 1, 2012
EXAMPLE 4 1 3 −6x − 21 = x + 2 2 +6x +6x Thursday, March 1, 2012
EXAMPLE 4 1 3 −6x − 21 = x + 2 2 +6x +6x 13 3 −21 = x + 2 2 Thursday, March 1, 2012
EXAMPLE 4 1 3 −6x − 21 = x + 2 2 +6x +6x 13 3 −21 = x + 2 2 3 3 − − 2 2 Thursday, March 1, 2012
EXAMPLE 4 1 3 −6x − 21 = x + 2 2 +6x +6x 13 3 −21 = x + 2 2 3 3 − − 2 2 45 13 − = x 2 2 Thursday, March 1, 2012
EXAMPLE 4 1 3 2 ⎛ 45 ⎞ ⎛ 13 ⎞ 2 −6x − 21 = x + ⎜ − 2 ⎟ = ⎜ 2 x ⎟ 13 2 2 13 ⎝ ⎠ ⎝ ⎠ +6x +6x 13 3 −21 = x + 2 2 3 3 − − 2 2 45 13 − = x 2 2 Thursday, March 1, 2012
EXAMPLE 4 1 3 2 ⎛ 45 ⎞ ⎛ 13 ⎞ 2 −6x − 21 = x + ⎜ − 2 ⎟ = ⎜ 2 x ⎟ 13 2 2 13 ⎝ ⎠ ⎝ ⎠ +6x +6x 45 13 3 x=− −21 = x + 13 2 2 3 3 − − 2 2 45 13 − = x 2 2 Thursday, March 1, 2012
EXAMPLE 4 1 3 2 ⎛ 45 ⎞ ⎛ 13 ⎞ 2 −6x − 21 = x + ⎜ − 2 ⎟ = ⎜ 2 x ⎟ 13 2 2 13 ⎝ ⎠ ⎝ ⎠ +6x +6x 45 13 3 x=− −21 = x + 13 2 2 ⎛ 45 ⎞ 1 ⎛ 45 ⎞ 3 3 3 −6 ⎜ − ⎟ − 21 = ⎜ − ⎟ + − − ⎝ 13 ⎠ 2 ⎝ 13 ⎠ 2 2 2 45 13 − = x 2 2 Thursday, March 1, 2012
EXAMPLE 4 1 3 2 ⎛ 45 ⎞ ⎛ 13 ⎞ 2 −6x − 21 = x + ⎜ − 2 ⎟ = ⎜ 2 x ⎟ 13 2 2 13 ⎝ ⎠ ⎝ ⎠ +6x +6x 45 13 3 x=− −21 = x + 13 2 2 ⎛ 45 ⎞ 1 ⎛ 45 ⎞ 3 3 3 −6 ⎜ − ⎟ − 21 = ⎜ − ⎟ + − − ⎝ 13 ⎠ 2 ⎝ 13 ⎠ 2 2 2 45 13 3 3 − = x − =− 2 2 13 13 Thursday, March 1, 2012
EXAMPLE 4 1 3 2 ⎛ 45 ⎞ ⎛ 13 ⎞ 2 −6x − 21 = x + ⎜ − 2 ⎟ = ⎜ 2 x ⎟ 13 2 2 13 ⎝ ⎠ ⎝ ⎠ +6x +6x 45 13 3 x=− −21 = x + 13 2 2 ⎛ 45 ⎞ 1 ⎛ 45 ⎞ 3 3 3 −6 ⎜ − ⎟ − 21 = ⎜ − ⎟ + − − ⎝ 13 ⎠ 2 ⎝ 13 ⎠ 2 2 2 45 13 3 3 − = x − =− 2 2 13 13 ⎛ 45 3 ⎞ ⎜ − 13 ,− 13 ⎟ ⎝ ⎠ Thursday, March 1, 2012
CHECK YOUR UNDERSTANDING p. 337 #1-4 Thursday, March 1, 2012
PROBLEM SET Thursday, March 1, 2012
PROBLEM SET p. 338 #5-31 odd, 49, 53 "Education's purpose is to replace an empty mind with an open one." – Malcolm Forbes Thursday, March 1, 2012

More Related Content

PDF
AS PHYSICS-May/June 9702/12
byHira Rizvi
 
PDF
Wintersemster 09/10 Strategic Management Englisch
byolafhengerer
 
PDF
Bayesian estimate for shape parameter from generalized power function distrib...
byAlexander Decker
 
PDF
11.fully invariant and characteristic interval valued intuitionistic fuzzy du...
byAlexander Decker
 
PDF
Fully invariant and characteristic interval valued intuitionistic fuzzy dual ...
byAlexander Decker
 
PDF
Geometry Section 3-4 1112
byJimbo Lamb
 
PDF
Geometry Section 6-5 1112
byJimbo Lamb
 
PDF
Geometry Section 5-3 11-12
byJimbo Lamb
 
AS PHYSICS-May/June 9702/12
byHira Rizvi
 
Wintersemster 09/10 Strategic Management Englisch
byolafhengerer
 
Bayesian estimate for shape parameter from generalized power function distrib...
byAlexander Decker
 
11.fully invariant and characteristic interval valued intuitionistic fuzzy du...
byAlexander Decker
 
Fully invariant and characteristic interval valued intuitionistic fuzzy dual ...
byAlexander Decker
 
Geometry Section 3-4 1112
byJimbo Lamb
 
Geometry Section 6-5 1112
byJimbo Lamb
 
Geometry Section 5-3 11-12
byJimbo Lamb
 

Viewers also liked

PDF
Geometry Section 3-2 1112
byJimbo Lamb
 
PDF
Geometry Section 6-4 1112
byJimbo Lamb
 
PDF
Geometry Section 6-2 1112
byJimbo Lamb
 
PDF
Geometry Section 5-1 1112
byJimbo Lamb
 
PDF
Geometry Section 4-3
byJimbo Lamb
 
PDF
Geometry Section 3-6 1112
byJimbo Lamb
 
PDF
Geometry Section 3-1 1112
byJimbo Lamb
 
PDF
Geometry Section 4-6 1112
byJimbo Lamb
 
PDF
Geometry Section 6-1 1112
byJimbo Lamb
 
PDF
Geometry Section 3-3 1112
byJimbo Lamb
 
PDF
Geometry Section 4-5 1112
byJimbo Lamb
 
PDF
Geometry Section 5-4 1112
byJimbo Lamb
 
PDF
Geometry section 4-1 1112
byJimbo Lamb
 
PDF
Geometry Section 4-2
byJimbo Lamb
 
PDF
Geometry Section 3-5 1112
byJimbo Lamb
 
PDF
Geometry Section 6-6 1112
byJimbo Lamb
 
PDF
Geometry Section 6-3 1112
byJimbo Lamb
 
PDF
Geometry Section 2-8 1112
byJimbo Lamb
 
PDF
Geometry Section 2-7 1112
byJimbo Lamb
 
PDF
Geometry Section 2-2 1112
byJimbo Lamb
 
Geometry Section 3-2 1112
byJimbo Lamb
 
Geometry Section 6-4 1112
byJimbo Lamb
 
Geometry Section 6-2 1112
byJimbo Lamb
 
Geometry Section 5-1 1112
byJimbo Lamb
 
Geometry Section 4-3
byJimbo Lamb
 
Geometry Section 3-6 1112
byJimbo Lamb
 
Geometry Section 3-1 1112
byJimbo Lamb
 
Geometry Section 4-6 1112
byJimbo Lamb
 
Geometry Section 6-1 1112
byJimbo Lamb
 
Geometry Section 3-3 1112
byJimbo Lamb
 
Geometry Section 4-5 1112
byJimbo Lamb
 
Geometry Section 5-4 1112
byJimbo Lamb
 
Geometry section 4-1 1112
byJimbo Lamb
 
Geometry Section 4-2
byJimbo Lamb
 
Geometry Section 3-5 1112
byJimbo Lamb
 
Geometry Section 6-6 1112
byJimbo Lamb
 
Geometry Section 6-3 1112
byJimbo Lamb
 
Geometry Section 2-8 1112
byJimbo Lamb
 
Geometry Section 2-7 1112
byJimbo Lamb
 
Geometry Section 2-2 1112
byJimbo Lamb
 

Similar to Geometry Section 5-2 1112

PDF
Medians & altitudes of a triangle
byA CM
 
PDF
Chapter 4
bykrishn_desai
 
PPT
Geometry 201 unit 5.4
byMark Ryder
 
PDF
Em03 t
bynahomyitbarek
 
PPTX
Triangle concurrency abmp oicc
byLaWanda King-Butler
 
PDF
Centroid of a Triangle Formula Properties and Example Questions.pdf
byChloe Cheney
 
PDF
4.5 Special Segments in Triangles
bysmiller5
 
PPTX
centroid theorem,Make a conjecture about the centroid of a triangle
byLiJiaxian
 
PDF
11X1 T08 01 angle theorems (2011)
byNigel Simmons
 
PDF
11x1 t07 01 angle theorems - 2012
byNigel Simmons
 
PDF
11 X1 T07 01 angle theorems (2010)
byNigel Simmons
 
PDF
Geom10.1-10.2
bykquarton
 
KEY
Calculus II - 33
byDavid Mao
 
PDF
Putting Objects in Perspective
byuisp dsin
 
PPT
TIU CET Review Math Session 3 Geometry by Young Einstein
byyoungeinstein
 
DOCX
Circle lesson plan, chords, arcs, segments, arcs
byMarvinMacan1
 
PPTX
Prove it!
byFrank Davis
 
PDF
Geom10.7
bykquarton
 
PPT
9 5 Inscribed Angles
byMr. Hohman
 
PPT
5-1, 5-2 Alt,Bisectors,Medians.ppt
bysmithj91
 
Medians & altitudes of a triangle
byA CM
 
Chapter 4
bykrishn_desai
 
Geometry 201 unit 5.4
byMark Ryder
 
Em03 t
bynahomyitbarek
 
Triangle concurrency abmp oicc
byLaWanda King-Butler
 
Centroid of a Triangle Formula Properties and Example Questions.pdf
byChloe Cheney
 
4.5 Special Segments in Triangles
bysmiller5
 
centroid theorem,Make a conjecture about the centroid of a triangle
byLiJiaxian
 
11X1 T08 01 angle theorems (2011)
byNigel Simmons
 
11x1 t07 01 angle theorems - 2012
byNigel Simmons
 
11 X1 T07 01 angle theorems (2010)
byNigel Simmons
 
Geom10.1-10.2
bykquarton
 
Calculus II - 33
byDavid Mao
 
Putting Objects in Perspective
byuisp dsin
 
TIU CET Review Math Session 3 Geometry by Young Einstein
byyoungeinstein
 
Circle lesson plan, chords, arcs, segments, arcs
byMarvinMacan1
 
Prove it!
byFrank Davis
 
Geom10.7
bykquarton
 
9 5 Inscribed Angles
byMr. Hohman
 
5-1, 5-2 Alt,Bisectors,Medians.ppt
bysmithj91
 

More from Jimbo Lamb

PDF
Geometry Section 1-5
byJimbo Lamb
 
PDF
Geometry Section 1-4
byJimbo Lamb
 
PDF
Geometry Section 1-3
byJimbo Lamb
 
PDF
Geometry Section 1-2
byJimbo Lamb
 
PDF
Geometry Section 1-2
byJimbo Lamb
 
PDF
Geometry Section 1-1
byJimbo Lamb
 
PDF
Algebra 2 Section 5-3
byJimbo Lamb
 
PDF
Algebra 2 Section 5-2
byJimbo Lamb
 
PDF
Algebra 2 Section 5-1
byJimbo Lamb
 
PDF
Algebra 2 Section 4-9
byJimbo Lamb
 
PDF
Algebra 2 Section 4-8
byJimbo Lamb
 
PDF
Algebra 2 Section 4-6
byJimbo Lamb
 
PDF
Geometry Section 6-6
byJimbo Lamb
 
PDF
Geometry Section 6-5
byJimbo Lamb
 
PDF
Geometry Section 6-4
byJimbo Lamb
 
PDF
Geometry Section 6-3
byJimbo Lamb
 
PDF
Geometry Section 6-2
byJimbo Lamb
 
PDF
Geometry Section 6-1
byJimbo Lamb
 
PDF
Algebra 2 Section 4-5
byJimbo Lamb
 
PDF
Algebra 2 Section 4-4
byJimbo Lamb
 
Geometry Section 1-5
byJimbo Lamb
 
Geometry Section 1-4
byJimbo Lamb
 
Geometry Section 1-3
byJimbo Lamb
 
Geometry Section 1-2
byJimbo Lamb
 
Geometry Section 1-2
byJimbo Lamb
 
Geometry Section 1-1
byJimbo Lamb
 
Algebra 2 Section 5-3
byJimbo Lamb
 
Algebra 2 Section 5-2
byJimbo Lamb
 
Algebra 2 Section 5-1
byJimbo Lamb
 
Algebra 2 Section 4-9
byJimbo Lamb
 
Algebra 2 Section 4-8
byJimbo Lamb
 
Algebra 2 Section 4-6
byJimbo Lamb
 
Geometry Section 6-6
byJimbo Lamb
 
Geometry Section 6-5
byJimbo Lamb
 
Geometry Section 6-4
byJimbo Lamb
 
Geometry Section 6-3
byJimbo Lamb
 
Geometry Section 6-2
byJimbo Lamb
 
Geometry Section 6-1
byJimbo Lamb
 
Algebra 2 Section 4-5
byJimbo Lamb
 
Algebra 2 Section 4-4
byJimbo Lamb
 

Recently uploaded

PPTX
Math 8 Quarter 4 Week 4-SECONDARY DATA.pptx
byshahanieabbat3
 
PPTX
Greengnorance Toolkit Module 6 Water Resources
byKarl Donert
 
PDF
Structure-of-the-Atom PPT.pdf/CBSE CLASS 11 CHEMISTRY/ PREPARED BY K SANDEEP ...
bySandeep Swamy
 
PPTX
How to Manage Reservation Method in Odoo 18 Inventory
byCeline George
 
PDF
Family and Marriage __ Sociology __ Jhasketan Kuanar __ NURSING VIBE ONLY .pdf
byJK NURSING VIBES ONLY JHASKETAN KUANAR
 
PPTX
PRE TERM LABOR ( PREMATURE LABOUR IN PREGNANCY)
byMuthu Kumar
 
PPTX
Methods & Applications of Enzyme Immobilization Technique.pptx
byAnupkumar Sharma
 
PPTX
How to Track & Manage My Time Section in Odoo 18 Time Off
byCeline George
 
PDF
Pharmaceutical Quality Assurance Unit 1 (BP606T)
byChetan Mali
 
PDF
How "Raiders of the Lost Ark" and "Ordinary People" Employ Non-Verbal Acting
by6x5csns4pn
 
PPTX
Renal Physiology- Functional anatomy of Kidney.pptx
byDisha Soriya
 
PPTX
Plant fibres used as surgical dressings & Sutures – Surgical Catgut and Ligat...
bySai Meer College of Pharmacy
 
PDF
Artificial Intelligence in Research and Academic Writing, Workshop on Researc...
byProf. Vinod Kumar Kanvaria
 
PDF
Bones by Sadu Kassam (play) story ppt pdf
byRonnieMaeBorres
 
PPTX
Greengnorance Toolkit Module1 Climate Change
byKarl Donert
 
PPTX
Plato's Insight model teaching and learning.pptx
byNikhitaDS
 
PPTX
Renal Physiology- Juxtaglomerular Apparatus.pptx
byDisha Soriya
 
PDF
Chapter 05 Drugs Acting on the Central Nervous System: Anticonvulsant (Antiep...
bySandeshSul
 
PPTX
WEEK 2 (2).pptx TLE COOKERY 10 QUARTER 4
byResynFayeCortez2
 
PPTX
How to perform product search based on a custom field from the Website Shop p...
byCeline George
 
Math 8 Quarter 4 Week 4-SECONDARY DATA.pptx
byshahanieabbat3
 
Greengnorance Toolkit Module 6 Water Resources
byKarl Donert
 
Structure-of-the-Atom PPT.pdf/CBSE CLASS 11 CHEMISTRY/ PREPARED BY K SANDEEP ...
bySandeep Swamy
 
How to Manage Reservation Method in Odoo 18 Inventory
byCeline George
 
Family and Marriage __ Sociology __ Jhasketan Kuanar __ NURSING VIBE ONLY .pdf
byJK NURSING VIBES ONLY JHASKETAN KUANAR
 
PRE TERM LABOR ( PREMATURE LABOUR IN PREGNANCY)
byMuthu Kumar
 
Methods & Applications of Enzyme Immobilization Technique.pptx
byAnupkumar Sharma
 
How to Track & Manage My Time Section in Odoo 18 Time Off
byCeline George
 
Pharmaceutical Quality Assurance Unit 1 (BP606T)
byChetan Mali
 
How "Raiders of the Lost Ark" and "Ordinary People" Employ Non-Verbal Acting
by6x5csns4pn
 
Renal Physiology- Functional anatomy of Kidney.pptx
byDisha Soriya
 
Plant fibres used as surgical dressings & Sutures – Surgical Catgut and Ligat...
bySai Meer College of Pharmacy
 
Artificial Intelligence in Research and Academic Writing, Workshop on Researc...
byProf. Vinod Kumar Kanvaria
 
Bones by Sadu Kassam (play) story ppt pdf
byRonnieMaeBorres
 
Greengnorance Toolkit Module1 Climate Change
byKarl Donert
 
Plato's Insight model teaching and learning.pptx
byNikhitaDS
 
Renal Physiology- Juxtaglomerular Apparatus.pptx
byDisha Soriya
 
Chapter 05 Drugs Acting on the Central Nervous System: Anticonvulsant (Antiep...
bySandeshSul
 
WEEK 2 (2).pptx TLE COOKERY 10 QUARTER 4
byResynFayeCortez2
 
How to perform product search based on a custom field from the Website Shop p...
byCeline George
 

Geometry Section 5-2 1112

  • 1.
    SECTION 5-2 Medians and Altitudes of Triangles Thursday, March 1, 2012
  • 2.
    ESSENTIAL QUESTIONS How do you identify and use medians in triangles? How do you identify and use altitudes in triangles? Thursday, March 1, 2012
  • 3.
    VOCABULARY 1. Median: 2. Centroid: 3. Altitude: 4. Orthocenter: Thursday, March 1, 2012
  • 4.
    VOCABULARY 1. Median: A segment in a triangle that connects a vertex to the midpoint of the opposite side 2. Centroid: 3. Altitude: 4. Orthocenter: Thursday, March 1, 2012
  • 5.
    VOCABULARY 1. Median: A segment in a triangle that connects a vertex to the midpoint of the opposite side 2. Centroid: The point of concurrency where the medians intersect in a triangle (always inside) 3. Altitude: 4. Orthocenter: Thursday, March 1, 2012
  • 6.
    VOCABULARY 1. Median: A segment in a triangle that connects a vertex to the midpoint of the opposite side 2. Centroid: The point of concurrency where the medians intersect in a triangle (always inside) 3. Altitude: A segment in a triangle that connects a vertex to the opposite side so that the side and altitude are perpendicular 4. Orthocenter: Thursday, March 1, 2012
  • 7.
    VOCABULARY 1. Median: A segment in a triangle that connects a vertex to the midpoint of the opposite side 2. Centroid: The point of concurrency where the medians intersect in a triangle (always inside) 3. Altitude: A segment in a triangle that connects a vertex to the opposite side so that the side and altitude are perpendicular 4. Orthocenter: The point of concurrency where the altitudes of a triangle intersect Thursday, March 1, 2012
  • 8.
    5.7 - CENTROIDTHEOREM The centroid of a triangle is two-thirds the distance from each vertex to the midpoint of the opposite side Thursday, March 1, 2012
  • 9.
    5.7 - CENTROIDTHEOREM The centroid of a triangle is two-thirds the distance from each vertex to the midpoint of the opposite side If G is the centroid of ∆ABC, then 2 2 2 AG = AF , BG = BD, and CG = CE 3 3 3 Thursday, March 1, 2012
  • 10.
    Special Segments andPoints in Triangles Point of Special Name Example Example Concurrency Property Perpendicular Circumcenter is Circumcenter equidistant from Bisector each vertex Angle In center is Incenter equidistant from Bisector each side Centroid is two- thirds the distance Median Centroid from vertex to opposite midpoint Altitudes are Altitude Orthocenter concurrent at orthocenter Thursday, March 1, 2012
  • 11.
    EXAMPLE 1 In ∆XYZ, P is the centroid and YV = 12. Find YP and PV. Thursday, March 1, 2012
  • 12.
    EXAMPLE 1 In ∆XYZ, P is the centroid and YV = 12. Find YP and PV. 2 YP = YV 3 Thursday, March 1, 2012
  • 13.
    EXAMPLE 1 In ∆XYZ, P is the centroid and YV = 12. Find YP and PV. 2 YP = YV 3 2 YP = (12) 3 Thursday, March 1, 2012
  • 14.
    EXAMPLE 1 In ∆XYZ, P is the centroid and YV = 12. Find YP and PV. 2 YP = YV 3 2 YP = (12) 3 YP = 8 Thursday, March 1, 2012
  • 15.
    EXAMPLE 1 In ∆XYZ, P is the centroid and YV = 12. Find YP and PV. 2 YP = YV PV = YV − YP 3 2 YP = (12) 3 YP = 8 Thursday, March 1, 2012
  • 16.
    EXAMPLE 1 In ∆XYZ, P is the centroid and YV = 12. Find YP and PV. 2 YP = YV PV = YV − YP 3 2 YP = (12) PV = 12 − 8 3 YP = 8 Thursday, March 1, 2012
  • 17.
    EXAMPLE 1 In ∆XYZ, P is the centroid and YV = 12. Find YP and PV. 2 YP = YV PV = YV − YP 3 2 YP = (12) PV = 12 − 8 3 YP = 8 PV = 4 Thursday, March 1, 2012
  • 18.
    EXAMPLE 2 In ∆ABC, CG = 4. Find GE. Thursday, March 1, 2012
  • 19.
    EXAMPLE 2 In ∆ABC, CG = 4. Find GE. 2 CG = CE 3 Thursday, March 1, 2012
  • 20.
    EXAMPLE 2 In ∆ABC, CG = 4. Find GE. 2 CG = CE 3 2 4 = CE 3 Thursday, March 1, 2012
  • 21.
    EXAMPLE 2 In ∆ABC, CG = 4. Find GE. 2 CG = CE 3 2 4 = CE 3 CE = 6 Thursday, March 1, 2012
  • 22.
    EXAMPLE 2 In ∆ABC, CG = 4. Find GE. 2 CG = CE GE = CE − CG 3 2 4 = CE 3 CE = 6 Thursday, March 1, 2012
  • 23.
    EXAMPLE 2 In ∆ABC, CG = 4. Find GE. 2 CG = CE GE = CE − CG 3 2 4 = CE GE = 6 − 4 3 CE = 6 Thursday, March 1, 2012
  • 24.
    EXAMPLE 2 In ∆ABC, CG = 4. Find GE. 2 CG = CE GE = CE − CG 3 2 4 = CE GE = 6 − 4 3 CE = 6 GE = 2 Thursday, March 1, 2012
  • 25.
    EXAMPLE 3 An artist is designing a sculpture that balances a triangle on tip of a pole. In the artistʼs design on the coordinate plane, the vertices are located at (1, 4), (3, 0), and (3, 8). What are the coordinates of the point where the artist should place the pole under the triangle so that is will balance? Thursday, March 1, 2012
  • 26.
    EXAMPLE 3 (1, 4), (3, 0), (3, 8) Thursday, March 1, 2012
  • 27.
    EXAMPLE 3 y (1, 4), (3, 0), (3, 8) x Thursday, March 1, 2012
  • 28.
    EXAMPLE 3 y (1, 4), (3, 0), (3, 8) x Thursday, March 1, 2012
  • 29.
    EXAMPLE 3 y (1, 4), (3, 0), (3, 8) x Thursday, March 1, 2012
  • 30.
    EXAMPLE 3 y (1, 4), (3, 0), (3, 8) We need to find the centroid, so we start by finding the midpoint of our vertical side. x Thursday, March 1, 2012
  • 31.
    EXAMPLE 3 y (1, 4), (3, 0), (3, 8) We need to find the centroid, so we start by finding the midpoint of our vertical side. x ⎛ 3 + 3 0 + 8⎞ M =⎜ , ⎟ ⎝ 2 2 ⎠ Thursday, March 1, 2012
  • 32.
    EXAMPLE 3 y (1, 4), (3, 0), (3, 8) We need to find the centroid, so we start by finding the midpoint of our vertical side. x ⎛ 3 + 3 0 + 8⎞ ⎛ 6 8⎞ M =⎜ , ⎟ = ⎜ 2 , 2⎟ ⎝ 2 2 ⎠ ⎝ ⎠ Thursday, March 1, 2012
  • 33.
    EXAMPLE 3 y (1, 4), (3, 0), (3, 8) We need to find the centroid, so we start by finding the midpoint of our vertical side. x ⎛ 3 + 3 0 + 8⎞ ⎛ 6 8⎞ M =⎜ , ⎟ = ⎜ 2 , 2⎟ ⎝ 2 2 ⎠ ⎝ ⎠ ( ) = 3,4 Thursday, March 1, 2012
  • 34.
    EXAMPLE 3 y (1, 4), (3, 0), (3, 8) We need to find the centroid, so we start by finding the midpoint of our vertical side. x ⎛ 3 + 3 0 + 8⎞ ⎛ 6 8⎞ M =⎜ , ⎟ = ⎜ 2 , 2⎟ ⎝ 2 2 ⎠ ⎝ ⎠ ( ) = 3,4 Thursday, March 1, 2012
  • 35.
    EXAMPLE 3 y (1, 4), (3, 0), (3, 8) We need to find the centroid, so we start by finding the midpoint of our vertical side. x ⎛ 3 + 3 0 + 8⎞ ⎛ 6 8⎞ M =⎜ , ⎟ = ⎜ 2 , 2⎟ ⎝ 2 2 ⎠ ⎝ ⎠ ( ) = 3,4 Thursday, March 1, 2012
  • 36.
    EXAMPLE 3 y x Thursday, March 1, 2012
  • 37.
    EXAMPLE 3 y Next, we need the distance from the opposite vertex to this midpoint. x Thursday, March 1, 2012
  • 38.
    EXAMPLE 3 y Next, we need the distance from the opposite vertex to this midpoint. d = (1 − 3)2 + (4 − 4)2 x Thursday, March 1, 2012
  • 39.
    EXAMPLE 3 y Next, we need the distance from the opposite vertex to this midpoint. d = (1 − 3)2 + (4 − 4)2 x = (−2) + 0 2 2 Thursday, March 1, 2012
  • 40.
    EXAMPLE 3 y Next, we need the distance from the opposite vertex to this midpoint. d = (1 − 3)2 + (4 − 4)2 x = (−2) + 0 2 2 = 4 Thursday, March 1, 2012
  • 41.
    EXAMPLE 3 y Next, we need the distance from the opposite vertex to this midpoint. d = (1 − 3)2 + (4 − 4)2 x = (−2) + 0 2 2 = 4 =2 Thursday, March 1, 2012
  • 42.
    EXAMPLE 3 y x Thursday, March 1, 2012
  • 43.
    EXAMPLE 3 y The centroid P is 2/3 of this distance from the vertex. x Thursday, March 1, 2012
  • 44.
    EXAMPLE 3 y The centroid P is 2/3 of this distance from the vertex. ⎛ 2 ⎞ P = ⎜1 + (2),4 ⎟ ⎝ 3 ⎠ x Thursday, March 1, 2012
  • 45.
    EXAMPLE 3 y The centroid P is 2/3 of this distance from the vertex. ⎛ 2 ⎞ P = ⎜1 + (2),4 ⎟ ⎝ 3 ⎠ x ⎛ 4 ⎞ P = ⎜1 + ,4 ⎟ ⎝ 3 ⎠ Thursday, March 1, 2012
  • 46.
    EXAMPLE 3 y The centroid P is 2/3 of this distance from the vertex. ⎛ 2 ⎞ P = ⎜1 + (2),4 ⎟ ⎝ 3 ⎠ x ⎛ 4 ⎞ P = ⎜1 + ,4 ⎟ ⎝ 3 ⎠ ⎛7 ⎞ P = ⎜ ,4 ⎟ ⎝3 ⎠ Thursday, March 1, 2012
  • 47.
    EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. Thursday, March 1, 2012
  • 48.
    EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y x Thursday, March 1, 2012
  • 49.
    EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y H J x I Thursday, March 1, 2012
  • 50.
    EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y H J x I Thursday, March 1, 2012
  • 51.
    EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y H J x I Thursday, March 1, 2012
  • 52.
    EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y To find the orthocenter, find the intersection of two altitudes. H J x I Thursday, March 1, 2012
  • 53.
    EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y To find the orthocenter, find the intersection of two altitudes. H J Let’s find the equations for the altitudes coming from I and H. x I Thursday, March 1, 2012
  • 54.
    EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y To find the orthocenter, find the intersection of two altitudes. H J Let’s find the equations for the altitudes coming from I and H. x I ( ) m JI = 1+ 3 −5 + 3 Thursday, March 1, 2012
  • 55.
    EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y To find the orthocenter, find the intersection of two altitudes. H J Let’s find the equations for the altitudes coming from I and H. x I ( ) m JI = 1+ 3 = 4 −5 + 3 −2 Thursday, March 1, 2012
  • 56.
    EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y To find the orthocenter, find the intersection of two altitudes. H J Let’s find the equations for the altitudes coming from I and H. x I ( ) m JI = 1+ 3 = 4 −5 + 3 −2 = −2 Thursday, March 1, 2012
  • 57.
    EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y To find the orthocenter, find the intersection of two altitudes. H J Let’s find the equations for the altitudes coming from I and H. x I ( ) m JI = 1+ 3 = 4 −5 + 3 −2 = −2 ⊥ m = 1 2 Thursday, March 1, 2012
  • 58.
    EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y To find the orthocenter, find the intersection of two altitudes. H J Let’s find the equations for the altitudes coming from I and H. x I ( ) m JI = 1+ 3 = 4 −5 + 3 −2 = −2 ⊥ m = 1 2 ( ) m HJ = 2 −1 1+ 5 Thursday, March 1, 2012
  • 59.
    EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y To find the orthocenter, find the intersection of two altitudes. H J Let’s find the equations for the altitudes coming from I and H. x I ( ) m JI = 1+ 3 = −5 + 3 −2 4 = −2 ⊥ m = 1 2 ( ) m HJ = 2 −1 1 1+ 5 6 = Thursday, March 1, 2012
  • 60.
    EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y To find the orthocenter, find the intersection of two altitudes. H J Let’s find the equations for the altitudes coming from I and H. x I ( ) m JI = 1+ 3 = −5 + 3 −2 4 = −2 ⊥ m = 1 2 ( ) m HJ = 2 −1 1 1+ 5 6 = ⊥ m = −6 Thursday, March 1, 2012
  • 61.
    EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y Altitude through H H J x I Thursday, March 1, 2012
  • 62.
    EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y Altitude through H 1 ⊥ m = , (1,2) H 2 J x I Thursday, March 1, 2012
  • 63.
    EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y Altitude through H 1 ⊥ m = , (1,2) H 2 J 1 y − 2 = (x −1) 2 x I Thursday, March 1, 2012
  • 64.
    EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y Altitude through H 1 ⊥ m = , (1,2) H 2 J 1 y − 2 = (x −1) 2 x 1 1 I y−2= x − 2 2 Thursday, March 1, 2012
  • 65.
    EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y Altitude through H 1 ⊥ m = , (1,2) H 2 J 1 y − 2 = (x −1) 2 x 1 1 I y−2= x − 2 2 1 3 y= x+ 2 2 Thursday, March 1, 2012
  • 66.
    EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y Altitude through I H J x I Thursday, March 1, 2012
  • 67.
    EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y Altitude through I ⊥ m = −6, (−3,−3) H J x I Thursday, March 1, 2012
  • 68.
    EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y Altitude through I ⊥ m = −6, (−3,−3) H y + 3 = −6(x + 3) J x I Thursday, March 1, 2012
  • 69.
    EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y Altitude through I ⊥ m = −6, (−3,−3) H y + 3 = −6(x + 3) J x y + 3 = −6x −18 I Thursday, March 1, 2012
  • 70.
    EXAMPLE 4 The vertices of ∆HIJ are H(1, 2), I(−3, −3), and J(−5, 1). Find the coordinates of the orthocenter of ∆HIJ. y Altitude through I ⊥ m = −6, (−3,−3) H y + 3 = −6(x + 3) J x y + 3 = −6x −18 I y = −6x − 21 Thursday, March 1, 2012
  • 71.
  • 72.
    EXAMPLE 4 1 3 −6x − 21 = x + 2 2 Thursday, March 1, 2012
  • 73.
    EXAMPLE 4 1 3 −6x − 21 = x + 2 2 +6x +6x Thursday, March 1, 2012
  • 74.
    EXAMPLE 4 1 3 −6x − 21 = x + 2 2 +6x +6x 13 3 −21 = x + 2 2 Thursday, March 1, 2012
  • 75.
    EXAMPLE 4 1 3 −6x − 21 = x + 2 2 +6x +6x 13 3 −21 = x + 2 2 3 3 − − 2 2 Thursday, March 1, 2012
  • 76.
    EXAMPLE 4 1 3 −6x − 21 = x + 2 2 +6x +6x 13 3 −21 = x + 2 2 3 3 − − 2 2 45 13 − = x 2 2 Thursday, March 1, 2012
  • 77.
    EXAMPLE 4 1 3 2 ⎛ 45 ⎞ ⎛ 13 ⎞ 2 −6x − 21 = x + ⎜ − 2 ⎟ = ⎜ 2 x ⎟ 13 2 2 13 ⎝ ⎠ ⎝ ⎠ +6x +6x 13 3 −21 = x + 2 2 3 3 − − 2 2 45 13 − = x 2 2 Thursday, March 1, 2012
  • 78.
    EXAMPLE 4 1 3 2 ⎛ 45 ⎞ ⎛ 13 ⎞ 2 −6x − 21 = x + ⎜ − 2 ⎟ = ⎜ 2 x ⎟ 13 2 2 13 ⎝ ⎠ ⎝ ⎠ +6x +6x 45 13 3 x=− −21 = x + 13 2 2 3 3 − − 2 2 45 13 − = x 2 2 Thursday, March 1, 2012
  • 79.
    EXAMPLE 4 1 3 2 ⎛ 45 ⎞ ⎛ 13 ⎞ 2 −6x − 21 = x + ⎜ − 2 ⎟ = ⎜ 2 x ⎟ 13 2 2 13 ⎝ ⎠ ⎝ ⎠ +6x +6x 45 13 3 x=− −21 = x + 13 2 2 ⎛ 45 ⎞ 1 ⎛ 45 ⎞ 3 3 3 −6 ⎜ − ⎟ − 21 = ⎜ − ⎟ + − − ⎝ 13 ⎠ 2 ⎝ 13 ⎠ 2 2 2 45 13 − = x 2 2 Thursday, March 1, 2012
  • 80.
    EXAMPLE 4 1 3 2 ⎛ 45 ⎞ ⎛ 13 ⎞ 2 −6x − 21 = x + ⎜ − 2 ⎟ = ⎜ 2 x ⎟ 13 2 2 13 ⎝ ⎠ ⎝ ⎠ +6x +6x 45 13 3 x=− −21 = x + 13 2 2 ⎛ 45 ⎞ 1 ⎛ 45 ⎞ 3 3 3 −6 ⎜ − ⎟ − 21 = ⎜ − ⎟ + − − ⎝ 13 ⎠ 2 ⎝ 13 ⎠ 2 2 2 45 13 3 3 − = x − =− 2 2 13 13 Thursday, March 1, 2012
  • 81.
    EXAMPLE 4 1 3 2 ⎛ 45 ⎞ ⎛ 13 ⎞ 2 −6x − 21 = x + ⎜ − 2 ⎟ = ⎜ 2 x ⎟ 13 2 2 13 ⎝ ⎠ ⎝ ⎠ +6x +6x 45 13 3 x=− −21 = x + 13 2 2 ⎛ 45 ⎞ 1 ⎛ 45 ⎞ 3 3 3 −6 ⎜ − ⎟ − 21 = ⎜ − ⎟ + − − ⎝ 13 ⎠ 2 ⎝ 13 ⎠ 2 2 2 45 13 3 3 − = x − =− 2 2 13 13 ⎛ 45 3 ⎞ ⎜ − 13 ,− 13 ⎟ ⎝ ⎠ Thursday, March 1, 2012
  • 82.
    CHECK YOUR UNDERSTANDING p. 337 #1-4 Thursday, March 1, 2012
  • 83.
  • 84.
    PROBLEM SET p. 338 #5-31 odd, 49, 53 "Education's purpose is to replace an empty mind with an open one." – Malcolm Forbes Thursday, March 1, 2012