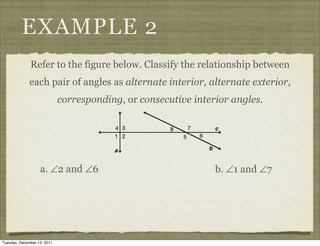
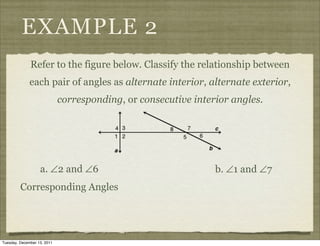
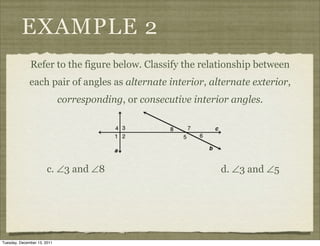
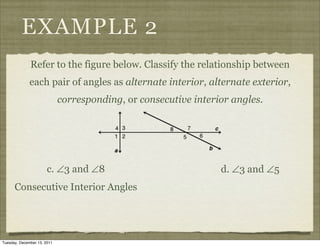
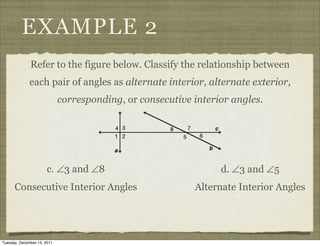
This document provides definitions and examples related to parallel and perpendicular lines. It defines parallel lines as lines in the same plane that do not intersect, and skew lines as lines in different planes that do not intersect. It also defines angles formed by parallel lines cut by a transversal, such as corresponding angles and alternate interior angles. Examples classify line segments and planes as parallel or skew, and identify angle relationships.

1. CHAPTER
3
Parallel and
Perpendicular Lines
Tuesday, December 13, 2011

2. SECTION 3-1
Parallel Lines and Transversals
Tuesday, December 13, 2011

3. ESSENTIAL
QUESTIONS
How do you identify the relationships between two lines or
two planes?
How do you name angle pairs formed by parallel lines and
transversals?
Tuesday, December 13, 2011

4. VOCABULARY
1. Parallel Lines:
2. Skew Lines:
3. Parallel Planes:
4. Transversal:
Tuesday, December 13, 2011

5. VOCABULARY
1. Parallel Lines: Two or more lines in the same plane that do not
intersect
2. Skew Lines:
3. Parallel Planes:
4. Transversal:
Tuesday, December 13, 2011

6. VOCABULARY
1. Parallel Lines: Two or more lines in the same plane that do not
intersect
2. Skew Lines: Two or more lines that are in different planes and
do not intersect
3. Parallel Planes:
4. Transversal:
Tuesday, December 13, 2011

7. VOCABULARY
1. Parallel Lines: Two or more lines in the same plane that do not
intersect
2. Skew Lines: Two or more lines that are in different planes and
do not intersect
3. Parallel Planes: Two or more planes that do not intersect
4. Transversal:
Tuesday, December 13, 2011

8. VOCABULARY
1. Parallel Lines: Two or more lines in the same plane that do not
intersect
2. Skew Lines: Two or more lines that are in different planes and
do not intersect
3. Parallel Planes: Two or more planes that do not intersect
4. Transversal: A line that intersects two other coplanar lines at
two different points
Tuesday, December 13, 2011

9. VOCABULARY
5. Interior Angles:
6. Exterior Angles:
7. Consecutive Interior Angles:
8. Alternate Interior Angles:
Tuesday, December 13, 2011

10. VOCABULARY
5. Interior Angles: Angles that are formed in the region between
two lines being intersected by a transversal
6. Exterior Angles:
7. Consecutive Interior Angles:
8. Alternate Interior Angles:
Tuesday, December 13, 2011

11. VOCABULARY
5. Interior Angles: Angles that are formed in the region between
two lines being intersected by a transversal
6. Exterior Angles: Angles that are formed in the region outside of
the two lines being intersected by a transversal
7. Consecutive Interior Angles:
8. Alternate Interior Angles:
Tuesday, December 13, 2011

12. VOCABULARY
5. Interior Angles: Angles that are formed in the region between
two lines being intersected by a transversal
6. Exterior Angles: Angles that are formed in the region outside of
the two lines being intersected by a transversal
7. Consecutive Interior Angles: Interior angles that are on the
same side of the transversal, thus being “next” to each other
8. Alternate Interior Angles:
Tuesday, December 13, 2011

13. VOCABULARY
5. Interior Angles: Angles that are formed in the region between
two lines being intersected by a transversal
6. Exterior Angles: Angles that are formed in the region outside of
the two lines being intersected by a transversal
7. Consecutive Interior Angles: Interior angles that are on the
same side of the transversal, thus being “next” to each other
8. Alternate Interior Angles: Nonadjacent interior angles that are
on opposite sides of the transversal
Tuesday, December 13, 2011

14. VOCABULARY
9. Alternate Exterior Angles:
10. Corresponding Angles:
Tuesday, December 13, 2011

15. VOCABULARY
9. Alternate Exterior Angles: Nonadjacent exterior angles that are
on opposite sides of the transversal
10. Corresponding Angles:
Tuesday, December 13, 2011

16. VOCABULARY
9. Alternate Exterior Angles: Nonadjacent exterior angles that are
on opposite sides of the transversal
10. Corresponding Angles: Angles that are on the same side of the
transversal and on the same side of the lines being intersected
by the transversal; these angles have the same position
Tuesday, December 13, 2011

17. EXAMPLE 1
Identify each of the following using the box.
a. All segments parallel to BC
b. A segment that is skew to EH
c. A plane that is parallel to plane ABG
Tuesday, December 13, 2011

18. EXAMPLE 1
Identify each of the following using the box.
a. All segments parallel to BC
FG, AD, EH
b. A segment that is skew to EH
c. A plane that is parallel to plane ABG
Tuesday, December 13, 2011

19. EXAMPLE 1
Identify each of the following using the box.
a. All segments parallel to BC
FG, AD, EH
b. A segment that is skew to EH
DC, CF, AB, or BG
c. A plane that is parallel to plane ABG
Tuesday, December 13, 2011

20. EXAMPLE 1
Identify each of the following using the box.
a. All segments parallel to BC
FG, AD, EH
b. A segment that is skew to EH
DC, CF, AB, or BG
c. A plane that is parallel to plane ABG
Plane DEC
Tuesday, December 13, 2011

21. EXAMPLE 2
Refer to the figure below. Classify the relationship between
each pair of angles as alternate interior, alternate exterior,
corresponding, or consecutive interior angles.
a. ∠2 and ∠6 b. ∠1 and ∠7
Tuesday, December 13, 2011

22. EXAMPLE 2
Refer to the figure below. Classify the relationship between
each pair of angles as alternate interior, alternate exterior,
corresponding, or consecutive interior angles.
a. ∠2 and ∠6 b. ∠1 and ∠7
Corresponding Angles
Tuesday, December 13, 2011

23. EXAMPLE 2
Refer to the figure below. Classify the relationship between
each pair of angles as alternate interior, alternate exterior,
corresponding, or consecutive interior angles.
a. ∠2 and ∠6 b. ∠1 and ∠7
Corresponding Angles Alternate Exterior Angles
Tuesday, December 13, 2011

24. EXAMPLE 2
Refer to the figure below. Classify the relationship between
each pair of angles as alternate interior, alternate exterior,
corresponding, or consecutive interior angles.
c. ∠3 and ∠8 d. ∠3 and ∠5
Tuesday, December 13, 2011

25. EXAMPLE 2
Refer to the figure below. Classify the relationship between
each pair of angles as alternate interior, alternate exterior,
corresponding, or consecutive interior angles.
c. ∠3 and ∠8 d. ∠3 and ∠5
Consecutive Interior Angles
Tuesday, December 13, 2011

26. EXAMPLE 2
Refer to the figure below. Classify the relationship between
each pair of angles as alternate interior, alternate exterior,
corresponding, or consecutive interior angles.
c. ∠3 and ∠8 d. ∠3 and ∠5
Consecutive Interior Angles Alternate Interior Angles
Tuesday, December 13, 2011

27. EXAMPLE 3
The driveways at a bus station are shown. Identify the
transversal connecting each pair of angles in the figure. Then
classify the relationship between each pair of angles.
a. ∠1 and ∠2 b. ∠2 and ∠3
Tuesday, December 13, 2011

28. EXAMPLE 3
The driveways at a bus station are shown. Identify the
transversal connecting each pair of angles in the figure. Then
classify the relationship between each pair of angles.
a. ∠1 and ∠2 b. ∠2 and ∠3
v; Corresponding
Tuesday, December 13, 2011

29. EXAMPLE 3
The driveways at a bus station are shown. Identify the
transversal connecting each pair of angles in the figure. Then
classify the relationship between each pair of angles.
a. ∠1 and ∠2 b. ∠2 and ∠3
v; Corresponding v; Alternate Interior
Tuesday, December 13, 2011

30. EXAMPLE 3
The driveways at a bus station are shown. Identify the
transversal connecting each pair of angles in the figure. Then
classify the relationship between each pair of angles.
c. ∠4 and ∠5
Tuesday, December 13, 2011

31. EXAMPLE 3
The driveways at a bus station are shown. Identify the
transversal connecting each pair of angles in the figure. Then
classify the relationship between each pair of angles.
c. ∠4 and ∠5
y; Consecutive Interior
Tuesday, December 13, 2011

32. CHECK YOUR
UNDERSTANDING
Check out the problems on p. 173 #1-12.
Tuesday, December 13, 2011

33. PROBLEM SET
Tuesday, December 13, 2011

34. PROBLEM SET
p. 174 #13-45 odd
“It has long been an axiom of mine that the little things are
infinitely the most important.” - Sir Arthur Conan Doyle
Tuesday, December 13, 2011